Уравнение импульсов Эйлера

Уравнение импульсов (количеств движения) Эйлера имеет важное значение для некоторых практических расчетов.

В механике материальной точки теорему импульсов формулируют так: « изменение проекции количества движения на какую-нибудь ось равно проекции импульса действующей силы на ту же ось»

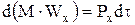. (1.16)

Применим эту теорему к элементарной струйке установившегося потока движущегося без трения (рис.1).

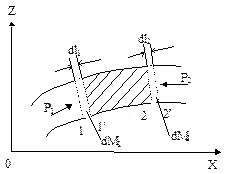
Рисунок 1

Рассмотрим проекции сил и количеств движения на ось Х. Ось Z направлена вверх. Следовательно, проекция силы тяжести на ось Х будет равна 0. Не равны нулю будут лишь проекции сил давления. За время dt объем, заключенный между сечениями 1 и 2 переместится в бесконечно близкое положение 1’ – 2’. Изменение количеств движения при переходе из положения 1 – 2 в положение 1’ – 2’ составит:

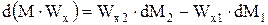. (1.17)

Так как на основании закона сохранения массы 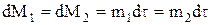, то уравнение (1.17) можно записать:

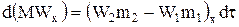. (1.18)

На рассматриваемый элемент струйки действуют только силы давления, поэтому проекция импульса силы на ось О–Х составит:

. (1.19)

Подставив равенства (1.18) и (1.19) в уравнение (1.16) получим уравнение импульсов (уравнение Эйлера) для струйки газа:

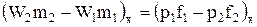. (1.20)

Поток газа складывается из отдельных струек, поэтому уравнение (1.20) справедливо для любого замкнутого контура, выделенного в потоке газа:

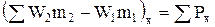(1.21)

Уравнение импульсов можно сформулировать так: разность количеств движения газа, вытекающего из контура и втекающего в него, спроектированных на какую-нибудь ось, равна сумме сил, действующих на этот контур, спроектированной на ту же ось.