Потери давления на предоление местных сопротивленй и на трение.

Рассмотрим, что представляет собой потерянное давление, входящее в уравнение Бернулли (1.25). Различают потери давления на преодоление местных сопротивлений и потери на трение.

Потери давления на местных сопротивлениях возникают при резком изменении величины скорости и направления движения газа. Это может быть резкое изменение сечения канала, поворот канала под всевозможными углами и т. д.

Потери давления на местных сопротивлениях определяют по формуле (Па):

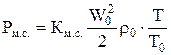, (1.26)

где К_м.с. – коэффициент местных сопротивлений, его величина зависит от формы местного сопротивления и, как правило, определяется опытным путем или по справочным таблицам;

r₀, W₀ – плотность и скорость газа при нормальных условиях, т. е. при атмосферном давлении 760 мм. рт. ст. и Т₀=273 К;

Т – действительная температура газа, К.

Если при движении газа по каналу, газопроводу местных сопротивлений нет, т. е. участок прямой, то все равно имеют место потери первоначального давления – это потери на трение. Потери давления на трение можно определить по следующей формуле (Па):

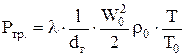, (1.27)

где l – коэффициент трения; l – длина канала, м; d_г– гидравлический диаметр канала, в случае некруглого сечения 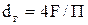_, F – площадь канала, м²; П – периметр канала, м.

Существуют эмпирические формулы для определения коэффициента трения. При ламинарном движении (Re£2100) коэффициент трения зависит от Re и не зависит от шероховатости стенок канала: .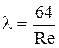

При турбулентном движении (Re³2300) коэффициент трения зависит не только от критерия Re, но и от относительной шероховатости стенки канала .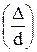

Если для гладких стенок при турбулентном движении 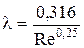, то для шероховатой поверхности ,

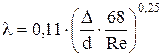где D – абсолютная шероховатость, мм; d – диаметр канала, мм;

При приближенных практических расчетах l можно принимать постоянным и равным для кирпичных каналов 0,05, для металлических 0,04.