Решение задач в Excel с помощью средств «Поиск решения» и «Подбор параметра»

Excel имеет большие возможности для работы с различными математическими средствами, позволяющими решать самые разнообразные инженерно-технические и научные задачи. Большинство из них не входят в базовый набор функций Excel, а подключаются дополнительно. Подключение осуществляется через кнопку Officeв меню кнопки Параметры Excel → Настройки. Выберите из меню строки Управление (нижний правый угол окна) Надстройки Excelи нажмите кнопку Перейти. В открывшемся окне выберите необходимые надстройки.

Основные надстройки, поставляемые вместе с пакетом Excel:

– Пакет анализа. Мощный инструмент обработки статистических данных, обеспечивающий дополнительные возможности для анализа.

– Мастер суммирования. Позволяет автоматизировать создание формул для суммирования данных в столбце таблицы и использовать частичные суммы.

– Мастер подстановок. Автоматизирует создание формулы для поиска данных в таблице по названию столбца и строки и позволяет использовать поиск с параметром.

– Поиск решения. Используется для решения уравнений и задач оптимизации.

Средство Поиск решения.Запускается командой Данные → Анализ → Поиск решения. Элементы диалогового окна:

установить целевую ячейку –адрес ячейки с целевой функцией;

равной – значение, к которому стремиться целевая функция;

изменяя ячейки –адреса влияющих ячеек;

параметры –открывает окно для задания ограничений на значения влияющих ячеек.

Средство Подбор параметра.Запускается командой Данные → Работа с данными → Анализ «что-если» → Подбор параметра.

Практическая часть

Задание 5.12. Решить систему нелинейных уравнений с помощью средства Поиск решения.

(1)

Выполнение.

В основу метода решения системы нелинейных уравнений положено то, что геометрически решения системы (1) описывают точки пересечения прямой ( 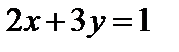) с окружностью ( 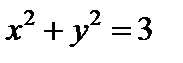) радиуса равному 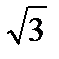. Решения заданной системы удовлетворяют и следующему уравнению:

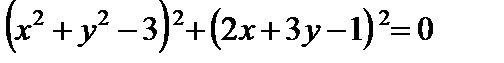(2)

Вместо системы (1) будем решать уравнение (2). Решений будет два.

Чтобы применить метод Поиск решения необходимо, предварительно, найти начальное приближение решений. Для этого построим таблицу значений левой части уравнения (2) по переменным х и у на интервале (– 1.7; +1.7) с шагом 0.3. Границы интервала взяты на основании того, что корни уравнения лежат внутри круга, радиус которого приблизительно равен 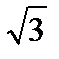=1.73.

Для построения таблицы выполняем:

1. В ячейки А2:А14 вводим значения х (в интервале [–1.7, 1.7]), а в ячейки В1:N1 – значения y в таком же интервале.

2. В ячейку В2 вводится формула =($A2^2+B$1^2-3)^2+(2*$A2+3*B$1-1)^2 –уравнение (2).

3. Копируем формулу ячейки B2 вдиапозон B2:N14.

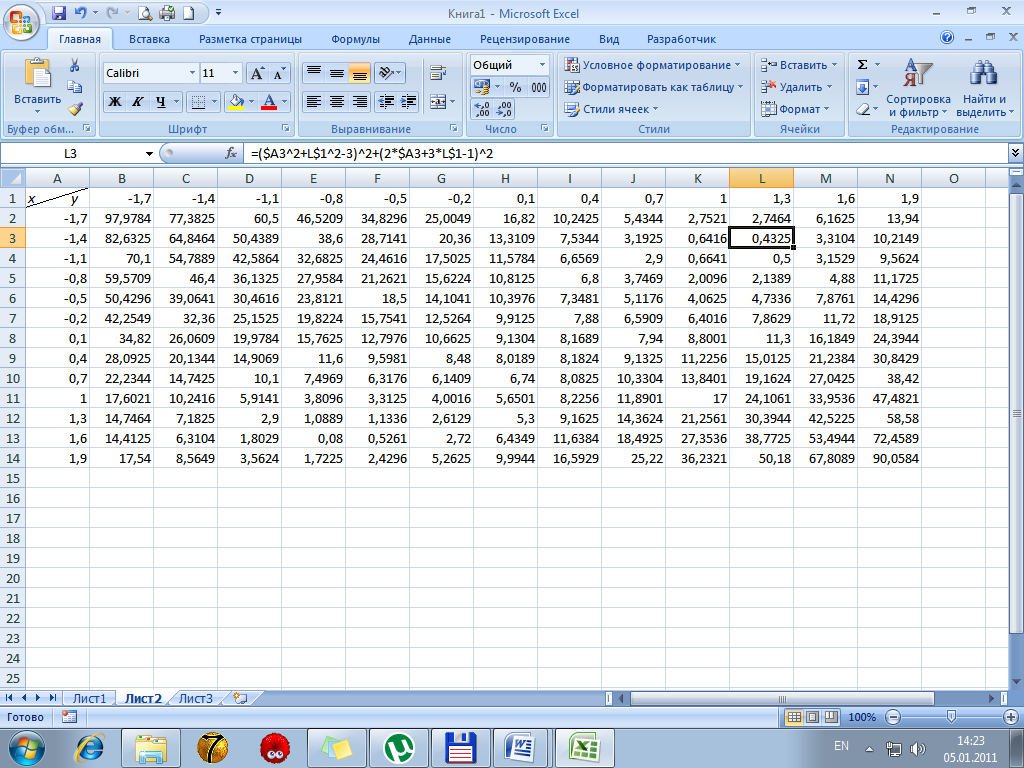
В соответствии с формулой (2) за начальные значения х и y берутся значения в тех ячейках заполненного диапазона, где функция принимает наименьшие значения. Под значения первого корня отводим ячейки А16:В16, а А17:В17 – под значения второго корня.

Для системы (1), в соответствии с полученной таблицей первое минимальное значение 0,4325. В ячейку А16мы вводим 1.3 – значение x, в В16 – 1.4 – значение y. В ячейку С16 вводим формулу =(А16^2+В16^2-3)^2+(2*A16+3*B16-1)^2.

Открываем окно Поиска решенийи устанавливаем: Целевая ячейка – $C16; Изменяя ячейки – $A16:$B16; установить параметр – Минимальному значению. Нажимаем кнопку Выполнить.

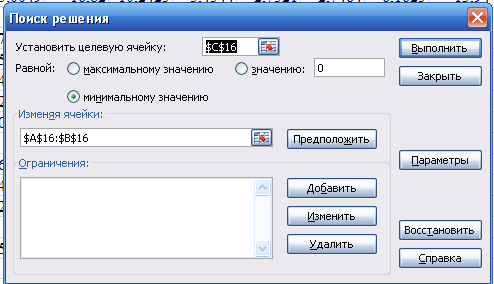
Значение корней уравнения появятся в ячейках А16 и В16. Второй корень находим аналогично, взяв следующее наименьшее значение 0,08.

Задание 5.13. Найти корни кубического уравнения (полинома) с одним неизвестным 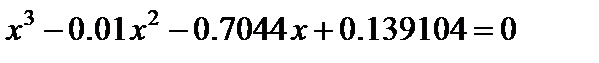с помощью средства Подбор параметра.

Выполнение.

Сначала находим интервалы, на которых существуют корни полинома. Такими интервалами, являются промежутки, на концах которых функция меняет знак. С этой целью построим таблицу значений полинома на интервале (-1,1) с шагом 0.2 и построим график. Для этого:

1. Введем в ячейку A2 значение –1 , а в A3 – значение: – 0.8.

2. Используя маркер заполнения, заполним ячейки до А12.

3. В ячейку B2 вводим формулу: = A2^3 – 0,01*A2^2 – 0,7044*A2 + 0,139104.

4. Заполняем диапазон B3:B12.

5. По полученным значениям строим график заданного полинома.

Мы увидим, что для нашего случая полином меняет знак на интервалах [-1,-0.8], [0.2, 0.4] и [0.6, 0.8], т.е. пересекается с осью x. Интервалов три – столько корней имеет уравнение третьей степени. Корни локализованы.

Теперь зададим точность нахождения значений корней. На вкладке Office → Параметры Excel → Формулы → Параметры вычислений задаем относительную погрешность 0,00001 и предельное число итераций 1000 (число последовательных приближений).

Отводим на новом рабочем листе ячейку С2 под первый корень, соответственно ячейки C3 и C4 под второй и третий корни полинома.

Корни будем находим методом последовательных приближений. Поэтому в ячейку С2 вводим сначала значение, являющееся первым приближением к искомому корню. В нашем случае возьмем первый отрезок и в нем среднее значение, т.е. – 0,9. Соответственно в ячейки С3 и С4 вводим приближенные значения для второго и третьего корней: +0,3 и +0,7.

Для нахождения корня с помощью Подбора параметра уравнение надо представить в таком виде, чтобы его правая часть не содержала переменную. В нашем примере этого не требуется. Отводим ячейку D2 под функцию, для которой ведется поиск первого корня. Причем вместо неизвестной x у этой функции должна указываться ссылка на ячейку, отведенную под искомый корень. Таким образом, в ячейку D2вводится формула:

= C2^3 – 0,01*C2^2 – 0,7044*C2 + 0.139104.

Копируем эту формулу в ячейки D3 и D4 для второго и третьего корней полинома. С помощью инструмента Подбор параметранаходим первый корень:

1. Выбираем команду Данные → Работа с данными → Анализ «что-если» → Подбор параметра. На экране появится диалоговое окно.

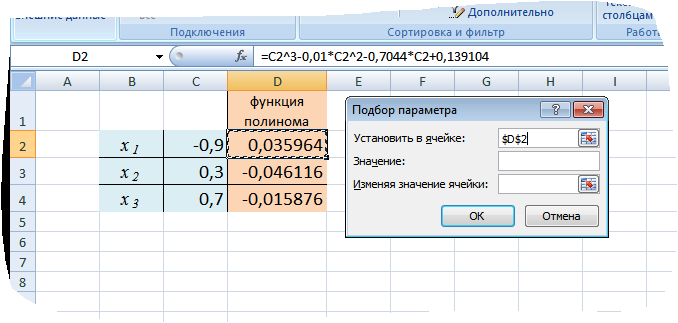
2. В поле Установить в ячейке введем ссылку на ячейку D2, в которой введена формула, вычисляющая значение левой части полинома.

3. В поле Значение вводим 0 – значение из правой части уравнения.

4. В поле Изменяя значение ячейки введем С2 –ссылка на ячейку, отведенную под первый корень.

5. Нажимаем ОК.

Получим окно с результатами:

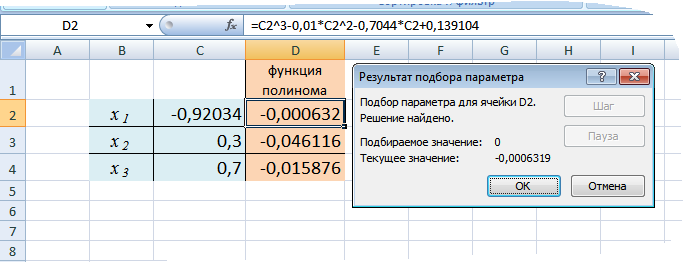
Закрыв окно, найденное приближенное значение корня помещается в ячейку D2. В данном случае оно равно –0,92034.

Аналогично, повторив действия 1–5 для каждого из оставшихся корней, в ячейках D3 и D4 находим их значения. Соответственно, они равны 0,21021 и 0,72071.