З’єднання автоматів
Існує декілька основних способів з'єднання автоматів.
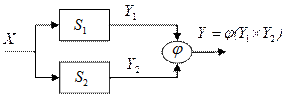
Паралельне з'єднання автоматів 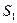 і
і 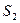 представлено на рис. 6.10, а. Є загальний вхідний алфавіт X і деякий пристрій
представлено на рис. 6.10, а. Є загальний вхідний алфавіт X і деякий пристрій  , об'єднуючий виходи автоматів:
, об'єднуючий виходи автоматів:
 :
: 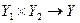 .
.
Автомати задані:
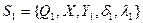 ,
,
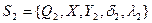 .
.
В результаті об'єднання отримуємо новий автомат 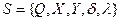 , для якого задані наступні параметри:
, для якого задані наступні параметри:
– множина станів 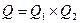 , утворюється з пар станів автоматів
, утворюється з пар станів автоматів 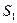 і
і 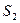 , тобто
, тобто 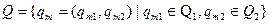 ;
;
– вхідний алфавіт X;
– вихідний алфавіт 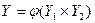 ;
;
– функція переходів, визначається правилом 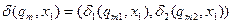 , де
, де 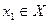 ;
;
– функція виходів, визначається правилом 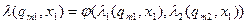 .
.
Нехай два автомати, що сполучаються паралельно, задані наступними таблицями: табл. 6.13 – 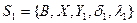 , табл. 6.14 –
, табл. 6.14 – 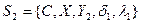 .
.
Таблиця 6.13.
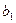
| 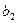
| 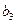
| |
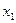
| 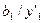
| 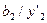
| 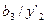
|
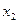
| 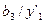
| 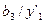
| 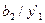
|
Таблиця 6.14.
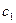
| 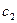
| |
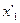
| 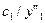
| 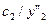
|
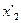
| 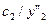
| 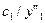
|
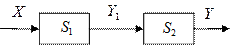
(а) (б)
(в)
Рис.6.10. З’єднання автоматів
Функція  перетворення виходів в об'єднаній схемі задана в табл. 6.15:
перетворення виходів в об'єднаній схемі задана в табл. 6.15:
Таблиця 6.15.
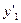
| 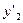
| |
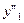
| 
| 
|
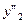
| 
| 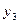
|
Отримуємо наступний результуючий автомат 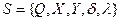 , для якого
, для якого
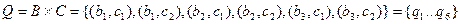 ,
,
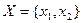 ,
,
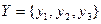 .
.
Функція переходів задається табл. 6.16.
Таблиця 6.16.
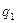
| 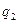
| 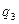
| 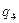
| 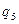
| 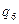
| |
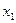
| 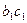
| 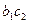
| 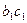
| 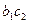
| 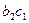
| 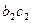
|
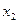
| 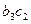
| 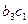
| 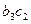
| 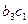
| 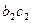
| 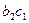
|
Тут, наприклад, 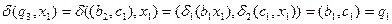 .
.
Функція виходів 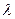 задається табл. 6.17:
задається табл. 6.17:
Таблиця 6.17.
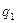
| 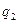
| 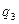
| 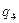
| 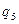
| 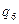
| |
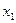
| 
| 
| 
| 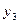
| 
| 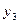
|
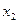
| 
| 
| 
| 
| 
| 
|
Тут, наприклад, 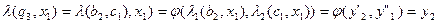 .
.
Послідовне з'єднання двох автоматів представлене на рис. 6.10, б. В цьому випадку перший автомат 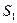 , другий автомат
, другий автомат 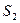 , тобто виходи першого автомата є входом другого. Результуючим автоматом послідовного з'єднання
, тобто виходи першого автомата є входом другого. Результуючим автоматом послідовного з'єднання 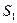 і
і 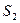 буде автомат
буде автомат 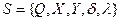 , для якого
, для якого
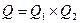 , або
, або 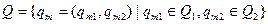 ;
;
Х = Х;
Y=Y;
функція переходів:
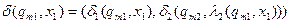 ,
,
або
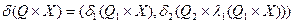 ;
;
функція виходів 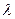 :
:
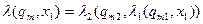 , або
, або 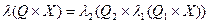 .
.
Як приклад розглянемо ті ж автомати 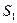 і
і 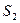 задані табл. 6.18, табл. 6.19.
задані табл. 6.18, табл. 6.19.
Таблиця 6.18.
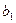
| 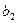
| 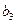
| |
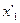
| 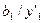
| 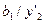
| 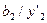
|
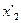
| 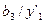
| 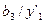
| 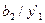
|
Таблиця 6.19.
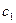
| 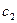
| |
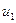
| 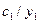
| 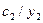
|
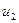
| 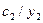
| 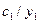
|
Результуючим автоматом послідовного з'єднання автоматів 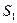 і
і 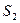 буде автомат, для якого:
буде автомат, для якого:
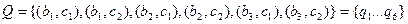 ;
;
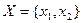 ;
;
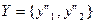 .
.
Функція переходів 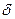 визначається табл. 6.20:
визначається табл. 6.20:
Таблиця 6.20.
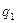
| 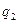
| 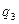
| 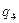
| 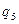
| 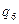
| |
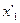
| 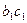
| 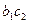
| 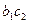
| 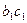
| 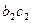
| 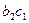
|
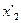
| 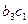
| 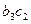
| 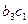
| 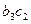
| 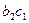
| 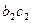
|
Тут, наприклад
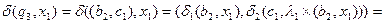
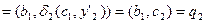 .
.
Функція виходів 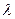 визначається табл. 6.21:
визначається табл. 6.21:
Таблиця 6.21.
| 
| 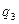
| 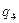
| 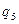
| 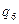
| |
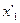
| 
| 
| 
| 
| 
| 
|
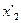
| 
| 
| 
| 
| 
| 
|
Тут, наприклад, 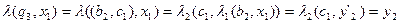 .
.
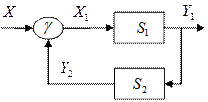
З'єднання автоматів із зворотним зв'язком представлене на рис. 6.10, в. В цьому випадку автомати 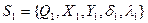 і
і 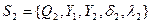 . Є деякий функціональний перетворювач
. Є деякий функціональний перетворювач 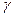 , що є автоматом без пам'яті, який реалізує відображення
, що є автоматом без пам'яті, який реалізує відображення 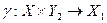 . В цьому випадку принаймні один з автоматів
. В цьому випадку принаймні один з автоматів 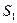 або
або 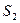 має бути автоматом Мура. Нехай
має бути автоматом Мура. Нехай 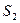 – автомат Мура, у якого
– автомат Мура, у якого 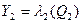 . Тоді результуючим автоматом такого з'єднання із зворотним зв'язком буде новий автомат
. Тоді результуючим автоматом такого з'єднання із зворотним зв'язком буде новий автомат 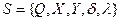 , для якого:
, для якого:
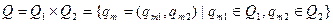 ;
;
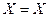 ;
;
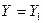 .
.
Функція переходів визначається таким чином:
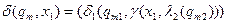 ,
, 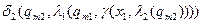 ,
,
або 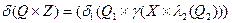 ,
, 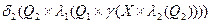 .
.
Функція виходів визначається таким чином:
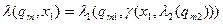 ,
,
або
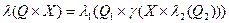 .
.
Як приклад розглянемо два автомати: 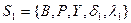 і
і 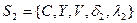 , які задані табл. 6.22 і табл. 6.23.
, які задані табл. 6.22 і табл. 6.23.
Таблиця 6.22.
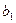
| 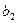
| 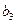
| |
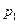
| 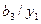
| 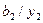
| 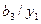
|
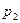
| 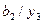
| 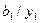
| 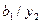
|
Таблиця 6.23.
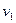
| 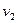
| |
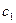
| 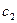
| |

| 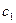
| 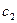
|

| 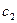
| 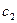
|
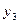
| 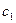
| 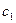
|
Функціональний перетворювач 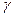 заданий в табл. 6.24.
заданий в табл. 6.24.
Таблиця 6.24.
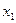
| 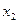
| 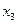
| |
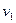
| 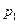
| 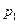
| 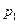
|
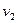
| 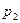
| 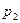
| 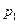
|
Результуючим автоматом з'єднання із зворотним зв'язком буде автомат 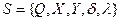 , для якого
, для якого
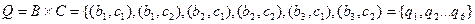 ;
;
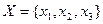 ;
;
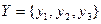 .
.
Функція переходів 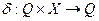 визначається таким чином (табл. 6.25):
визначається таким чином (табл. 6.25):
Таблиця 6.25.
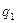
| 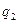
| 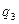
| 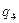
| 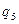
| 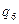
| |
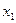
| 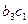
| 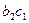
| 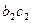
| 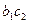
| 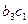
| 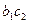
|
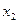
| 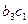
| 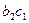
| 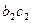
| 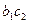
| 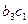
| 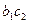
|
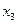
| 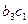
| 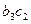
| 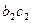
| 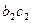
| 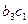
| 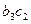
|
Тут, наприклад,
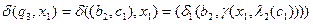 ;
;
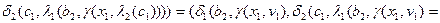
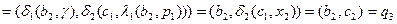 .
.
Функції виходів 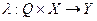 задається табл. 6.26:
задається табл. 6.26:
Таблиця 6.26.
| 
| 
| 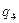
| 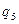
| 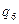
| |
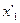
| 
| 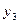
| 
| 
| 
| 
|
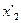
| 
| 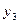
| 
| 
| 
| 
|
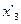
| 
| 
| 
| 
| 
| 
|
В цьому випадку:
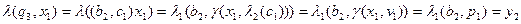 .
.
Дата добавления: 2016-09-26; просмотров: 1924;











