Використання теореми Шенона при синтезі скінченних автоматів на основі JK-тригерів
Як відомо, характеристичне рівняння JK-тригера має вигляд:
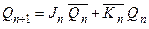 . .
|
Звернемо тепер увагу на теорему Шенона:
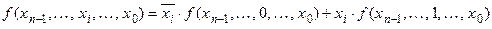 . .
| (7.1) |
Зрозуміло, що функції 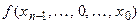 і
і  – це різні функції, тому позначимо їх відповідно як функції
– це різні функції, тому позначимо їх відповідно як функції 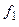 та
та 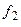 , а формулу (7.1) перепишемо у вигляді:
, а формулу (7.1) перепишемо у вигляді:
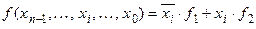 . .
|
Тепер звернемо увагу на той факт, що функцію переходів будь-якого тригера скінченного автомата можемо розглядати як функцію вигляду:
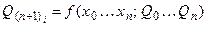 , ,
|
тому, розглядаючи її в відповідності до теореми Шенона, відносно стану заданого i-го тригера, отримуємо:
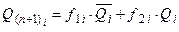 , ,
| (7.2) |
де, зрозуміло, функції 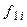 та
та 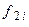 вже не містять відповідно змінних
вже не містять відповідно змінних 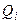 та
та 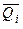 .
.
Порівнюючи тепер характеристичне рівняння JK-тригера з формулою (7.2), бачимо, що:
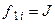 і і 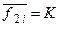 . .
|
Звідси витікає, що, прийнявши в функції переходів тригера  , отримуємо функцію збудження для входу J-:
, отримуємо функцію збудження для входу J-:
 , ,
|
а, прийнявши 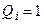 , отримуємо функцію збудження для входу К-:
, отримуємо функцію збудження для входу К-:
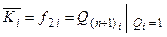 або або 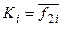 . .
|
Розглянемо приклад. Потрібно розробити автомат, який би в залежності від керуючого сигналу G міг працювати як двійковий лічильник 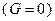 або як лічильник з відліком в відповідності до коду Грея з
або як лічильник з відліком в відповідності до коду Грея з 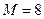
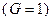 . Автомат розробити з використанням JK-тригерів.
. Автомат розробити з використанням JK-тригерів.
Таблиця переходів автомата має вигляд табл. 7.20.
Таблиця 7.20.
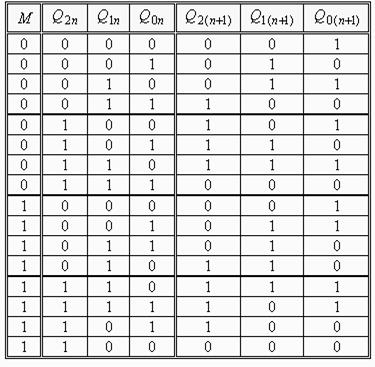
Рівняння переходів кожного з тригерів:
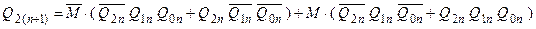 ; ;
|
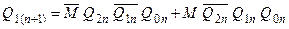 ; ;
|
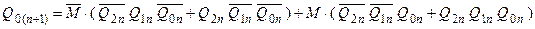 . .
|
Функції збудження для входів J- і K-:
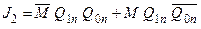 ; ;
| 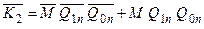 ; ;
|
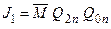 ; ;
| 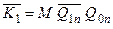 ; ;
|
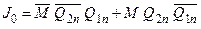 ; ;
| 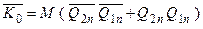 . .
|
Читачам пропонується самостійно побудувати принципову схему синтезованого цифрового автомата в відповідності до цих функцій.
Дата добавления: 2016-09-26; просмотров: 1685;











