Загальна характеристика скінченних автоматів

Розглянуті схеми тригерів та інших схем на їх основі передбачають наявність у тригері двох станів. Реакція пристрою на вхідні логічні сигнали залежить від того, в якому стані знаходиться тригер. Але існує велика кількість різноманітних схем, у яких використовується декілька тригерів. У такому випадку кількість внутрішніх станів схеми зростає в пропорції 2^m, де m – кількість тригерів. При цьому, зрозуміло, зростає складність “реакції” такого пристрою на вхідні сигнали, оскільки кожного разу внутрішні стани тригерів можуть бути іншими.

Цифрові пристрої з m тригерами (m > 1), стан виходів яких залежить не тільки від значень вхідних сигналів у заданий момент часу, а й від стану використовуваних тригерів у даний та попередній моменти часу, називаються цифровими автоматами.

У загальному плані цифровим автоматом називається пристрій, який формує ряд вихідних дискретних сигналів у відповідності із вхідною бінарною комбінацією сигналів. Найпростішим з таких автоматів є перетворювач кодів, і він називається комбінаційним.

У подальшому розглядатимуться автомати з пам’яттю, завдяки якій значення їх виходів залежать не лише від вхідних сигналів, що надходять у визначений момент часу, а також від внутрішнього стану автомата. Оскільки кількість внутрішніх станів залежить від кількості використовуваних тригерів, то цифрові автомати поділяються на скінченні, що мають обмежену кількість станів, і автомати з нескінченною кількістю станів,або послідовнісні машини. До останніх відносяться ЕОМ.

Будь-який цифровий автомат є сукупністю елементів пам’яті (тригерів) та комбінаційних схем. Тригери містять інформацію про особливості попередньої роботи автомата. Комбінаційні схеми на основі вхідних автоматів та інформації, яка береться з тригерів, формують вихідні сигнали і сигнали для формування нових станів тригерів. Таким чином, однією з особливостей цифрових автоматів є те, що вони мають свої внутрішні стани, від яких залежить реакція на вхідні сигнали. Одним з найпростіших прикладів цифрових автоматів є кодовий замок, реакція на черговий сигнал якого залежить від попередніх сигналів.

Скінченні автомати можуть бути синхронними, зміна станів яких відбувається в тактові моменти часу, що задаються зовнішнім генератором. В асинхронних автоматах зміна станів відбувається внаслідок дії вхідних сигналів без затримок. Тому асинхронні автомати вважаються більш швидкодіючими і знаходять використання у швидкодіючих інформаційних пристроях вимірювання і керування різноманітними процесами, де необхідна миттєва реакція на зміну вхідних сигналів.

Синхронні автомати в силу специфіки своєї роботи вносять у процес вимірювання або керування затримку, що визначається величиною періоду синхросигналу.

Здебільшого асинхронні автомати будуються на основі асинхронних елементів пам’яті – асинхронних тригерів. Синхронні автомати будуються з використанням синхронних тригерів.

Математичною моделлю цифрового автомата є абстрактний автомат, в якому враховуються його вхідні та вихідні сигнали, а також внутрішні стани. Будемо розглядати детерміновані автомати, які завжди мають початковий стан Q₀ , з якого починають працювати при дії вхідних сигналів і при повторі перебору вхідних сигналів повторюють послідовність станів і вихідних сигналів.

Абстрактний автомат задається множиною внутрішніх станів 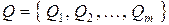(алфавітом станів), множиною вхідних сигналів 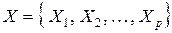(вхідним алфавітом), множиною вихідних сигналів 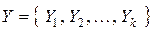(вихідним алфавітом) і початковим станом Q₀ . Перехід з одного стану в інший визначається функцією переходів f_p , що визначає стан автомата Q_s , в який він переходить з попереднього стану Q_m при дії сигналу X_p :

.

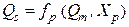Значення виходів автомата задається функцією виходів λ, що залежить від стану автомата Q_m і вхідного сигналу X_p :

.

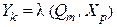Абстрактний автомат працює в дискретному часі, який задається цілими позитивними числами t = 0, 1, 2, …

У кожний момент дискретного часу t, який зветься тактом, автомат перебуває у деякому стані 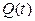з множини станів автомата Q.

У початковий момент часу (t = 0) він завжди знаходиться в стані Q(0) = Q₀ . Вважається, що реакція автомата на вхідні сигнали не залежить від інтервалів часу між тактовими моментами часу.

У момент t, знаходячись у стані Q(t), автомат сприймає на своєму вході сигнали, які називаються буквами (літерами) вхідного алфавіту 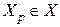. У відповідності до функції переходів 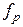, він перейде у стан 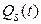, що описується алфавітом станів, тобто .

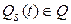Аналогічно, у відповідності з функцією виходів 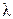, на виході отримається сигнал 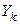, де .

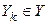Розглянемо RS-тригер як скінчений автомат. RS-тригер має два стани із множини станів Q : Q₁ = 0 і Q₂ = 1, де Q₁, Q₂ 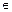Q. Автомат має чотири значення входів X_p з алфавіту входів X₁ , X₂ , X₃ , X₄ , де 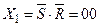; ; 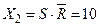; 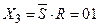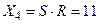. Вихідної комбінаційної логіки автомат не має, тобто залежність 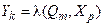визначається формулою: Y = Q.

Скінчена множина букв вхідного алфавіту, вихідного алфавіту і станів називається словами. Для скінченого автомата кількість символів цих алфавітів обмежена і однакова. Повний перебір символів вхідного слова повинен привести автомат до початкового стану Q₀ . Автомат, який завжди починає працювати з початкового стану, називається ініціальним.

Поняття станів в описі автоматів пов’язане з необхідністю враховувати типи і характер попередніх сигналів, тобто сигналів, які діяли на один або декілька тактів раніше. Стани автомата і є тими відповідними елементами пам’яті, що характеризують попередні сигнали. Введення поняття станів дозволяє усунути час як явну змінну і визначати вихідний сигнал як функцію внутрішнього стану і входу в тактовий момент часу. Такий спосіб опису автоматів має великі переваги перед іншими для асинхронних пристроїв, в яких інтервали часу між сусідніми тактами можуть мати довільні значення, що значно відрізняються між собою. З такої точки зору комбінаційні пристрої відносяться до автоматів, в яких вихід не залежить від попередніх сигналів і повністю визначається комбінацією вхідних сигналів.

У практиці роботи автоматів часто мають місце випадки, коли деякі комбінації значень вхідних символів подавати неприпустимо (згадаємо таблицю станів RS-тригера). Такі комбінації є забороненими для автомата. Автомати, що мають заборонені вхідні слова, називаються частковими. Наприклад, деякий абстрактний автомат має вхідний алфавіт Х, що складається з двох символів Х₀ і Х₁, кожен з яких може приймати значення 0 або 1. Слова 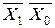, , 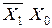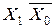є дозволеними, а слово X₁ X₀ – забороненим.

Наявність заборонених станів зменшує кількість слів вхідного алфавіту, зменшує кількість станів і дозволяє будувати часткові автомати з меншими затратами, ніж повні, для яких вказаних обмежень не існує.

Функція 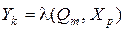задає значення виходів автомата з алфавіту Y. Кількість символів алфавіту Y не співпадає з кількістю символів алфавіту Х. За аналогією з перетворювачами кодів, автомат забезпечує відображення слів вхідного алфавіту в слова вихідного алфавіту. Якщо прийняти можливу кількість слів вхідного алфавіту за P_x , вихідного алфавіту за K_y , то в залежності від співвідношення між P_x та K_y автомати можуть за функціональним призначенням розділятися на три групи.

При K_y < P_x маємо автомати, які призначені для розв’язання задач керування, стиснення інформації, розпізнавання повідомлень. Наприклад, цифровий кодовий замок може мати 3…5 вхідних символів і лише один вихідний. Інший приклад – розпізнавання введеного пароля при вході в комп’ютер.

Якщо K_y > P_x , то маємо ситуацію, коли довжина вихідних слів буде більшою, ніж вхідних, оскільки кількість слів повинна бути однаковою. Тобто вихідні слова будуть нести збиткову інформацію, що використовується, як відмічалося в попередніх розділах, для синтезу перешкодостійких кодів.

При K_y = P_x кількість і довжина вхідних і вихідних слів однакові. Такі автомати використовуються для деяких кодових перетворень (наприклад, перетворення двійкового коду в код Грея, і т. д.), для реалізації деяких методів захисту даних від несанкціонованого доступу (метод підстановок) і т. п.