Кодування станів автомата
Найважливішою задачею, що має місце при кодуванні станів автомата є виключення значень його елементів пам’яті при заданих переходах. Таке кодування називається протигоночним. Найпростіший спосіб протигоночного кодування є сусіднє кодування, при якому два стани, що пов’язані між собою простими переходами кодуються наборами війкових чисел, що відрізняються станом лише одного ЕП. Основними вимогами до автомата, в якому забезпечується сусіднє кодування станів є:
– в графі автомата не повинно бути замкнутих контурів, що містять непарну кількість вершин;
– два сусідні стани другого порядку не повинні мати більше двох станів, що лежать між ними. При цьому під станами другого порядку маються на увазі два стани, шлях між якими по графу автомата складається з двох ребер (незалежно від орієнтації). На рис. 6.6 зображені два графа, які не задовольняють вказаним вимогам і не можуть бути закодовані сусідніми кодами.
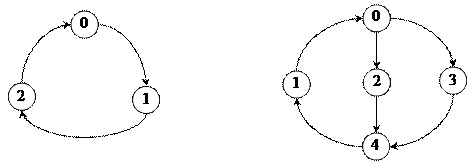
Рис.6.6.
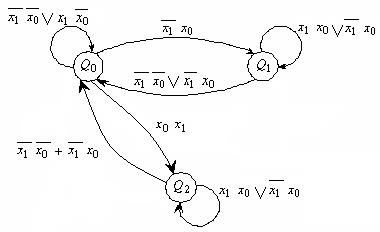
Граф переходів для генератора з забороною (табл. 6.6) зображено на рис. 6.7. В розглянутому випадку граф має непарну кількість вершин, але контур незамкнений. Один з варіантів кодування станів приводить до табл. 6.9.
Таблиця 6.9.
| Стани | Код q1 q2 |
| Q0 | 0 0 |
| Q1 | 0 1 |
| Q2 | 1 0 |
Рис. 6.7.
Після закінчення кодування станів будується закодована таблиця переходів автомата, що проектується. Для цього в скороченій таблиці переходів замінюються назви переходів їх кодовими значеннями. Табл. 6.6 автомата, що розглядається, прийме вигляд, зображений у табл. 6.10.
Таблиця 6.10.
| X Q | x1x0 | Y | |||
| q1 q2 | |||||
| 0 0 | |||||
| 0 1 | |||||
| 1 0 |
Розглянемо наступний приклад. Необхідно побудувати граф переходів і виконати сусіднє кодування для автомата, скорочена таблиця переходів якого відповідає табл. 6.8.
Граф переходів, побудований до табл. 6.8 зображений на рис. 6.8. Закодуємо стани в відповідності до табл. 6.11.
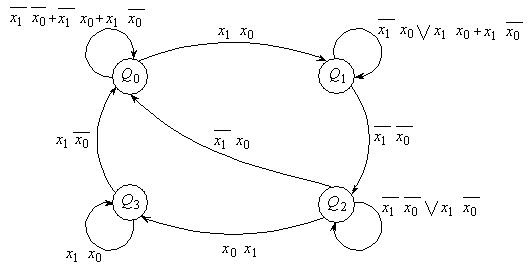
Рис.6.8.
Таблиця 6.11.
| Стани | Код q1 q2 |
| Q0 | 0 0 |
| Q1 | 0 1 |
| Q2 | 1 1 |
| Q3 | 1 0 |
При такому кодуванні маємо перехід з Q2 в Q0 , тобто з 11 в 00, який не відповідає умові сусіднього кодування.
Для розв’язання такої проблеми перехід з Q2 в Q0 необхідно зробити більш складним, через Q3 зробивши Q3 нестійким станом для даної комбінації сигналів. Граф-схема автомата прийме вигляд, зображений на рис. 6.9.
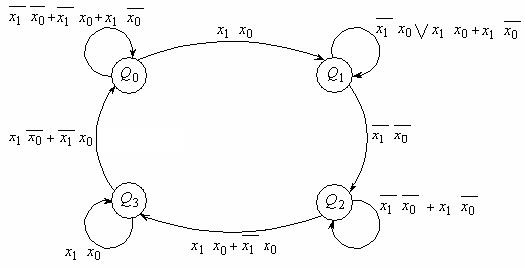
Рис.6.9.
Для забезпечення такої заміни необхідно зробити відповідні зміни в скороченій таблиці переходів при Q=3 і x1x2=01 замінити стан 1 на стан 4.
Для отримання чотирьох станів автомата необхідно мати два елементи пам’яті. Забезпечивши кодування станів, таблиця переходів в табл. 6.8 також може бути зображена в закодованому вигляді (див. табл. 6.12).
Таблиця 6.12.
| X Q | x1x0 | Y | |||
| q1 q2 | |||||
| 0 0 | |||||
| 0 1 | |||||
| 1 1 | |||||
| 1 0 | – | – |
Дата добавления: 2016-09-26; просмотров: 2972;











