Энтропия источника сообщений

В теории информации принят энтропийный подход к измерению количества информации. Развивая и обобщая идеи Р. Хартли, К. Шеннон в 1948 г. в своем фундаментальном труде «Математическая теория связи» ввел очень важное понятие энтропии источника сообщений.

В общем случае передаваемое по каналам связи сообщение можно представить в виде набора некоторых смысловых элементов или символов (например, букв) какого-либо алфавита Х. Пусть объем (полное число символов) алфавита равно m. Положим, что величины всех вероятностей появления любого из символов Р_i (i= 1, 2, ... m) – априорные, т.е. известные.

Энтропией источника сообщений называют среднее значение количества информации, приходящееся на один символ алфавита (бит/символ):

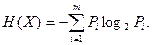(12.3)

При этом, буква Х в обозначении энтропии Н(Х) указывает на определенный источник с алфавитом Х. Энтропию можно рассматривать как числовую характеристику закона распределения, выражающую неопределенность, которая присуща элементам алфавита, выбранного для передачи сообщений. Свойства понятия энтропия.

1. Энтропия является положительной непрерывной величиной. Пусть сообщение передается с помощью двоичного алфавита (двоичного источника), состоящего только из двух символов, например, 0 и 1. Если вероятность появления первого символа равна Р, то вероятность появления второго символа 1 – Р. В этом случае энтропия изменяется от 0 до 1 и

Н(Х) = – Р log₂P–(1–P)log₂(1– P). (12.4)

На рис. 12.1 приведена зависимость Н(Х) для двоичного источника , построенная по (12.4). Она показывает, что максимальное значение энтропии

Н(Х) = 1 бит/символ достигается при равновероятном появлении обеих букв алфавита. Если же Р приближается к 0 или 1, то энтропия источника становится низкой. Сообщение превращается в детерминированную последовательность символов.

2. Энтропия равна нулю тогда и только тогда, когда вероятность одного из состояний равна единице. Это соответствует случаю, когда одно из состояний источника сообщения достоверно, т.е. отсутствует какая-либо неопределенность.

3. Энтропия максимальна, когда все символы источника сообщений равновероятны, т.е. Р₁ = Р₂ = ...= Р_m =1/m . В этом случае

Н(Х) = log₂m = I (12.5)

Теперь с помощью свойств 1-3 можно дать другое общепринятое определение и наглядно пояснить смысл понятия энтропия. Энтропия – это средняя информативность источника на один символ, определяющая «непредсказуемость» или «неожиданность» выдаваемых им сообщений. Полностью детерминированный источник, вырабатывающий лишь одну, заранее известную последовательность символов, обладает нулевой информативностью. И наоборот, наиболее «хаотический» источник, выдающий взаимно независимые и равновероятные символы, обладает максимальной информативностью.

Используя соотношение (12.5) можно легко вывести формулу Хартли для определения количества информации дискретных сообщений. Если объем алфавита символов равен m, а каждое сообщение составлено из n элементов, то число возможных сообщений N = mⁿ и количество информации:

I = log₂N = log₂mⁿ = nlog₂m. (12.6)

ПРИМЕР 12.1

Вычислить энтропию источника, который может выдавать четыре символа с равной вероятностью появления.

Р е ш е н и е. Используя формулу (12.5), получаем:

Н(Х) = log₂m = log₂4 = 2 бита.