Кодирование сообщений в системах связи

К.Э.Шеннон в 1948 году в своем труде «Математическая теория связи» впервые доказал, что абсолютно надежно передавать информацию по каналам связи с помехами можно не за счет увеличения мощности сигнала или уменьшения скорости передачи, а за счет усложнения методов модуляции-демодуляции и введения кодирования сообщений.

Преобразование сообщения в радиосигнал в системах связи осуществляется в виде двух операций – кодирования и модуляции. С их помощью источник сообщения согласуется с каналом связи.

В теории передачи информации под кодированием в широком смысле понимают преобразование сообщения в сигнал для передачи его по каналу связи. На практике под словом кодирование подразумевается кодирование в узком смысле – преобразование сообщений дискретного источника для передачи их по дискретному каналу. Система кодирования – совокупность правил кодового обозначения объектов.

Сообщение может иметь как аналоговую, так и дискретную форму. Простейшим примером дискретного сообщения является текст. Любой текст представляет собой определенное число элементов: букв, цифр, знаков препинания, их совокупность называется алфавитом источника сообщения. Поскольку число элементов в каждом алфавите конечно, то их можно пронумеровать, т.е. закодировать, и тогда передача сообщения сведется к передаче последовательности чисел.

Теоретически в качестве основания счисления можно принять любое целое число m и тогда представить число N как:

N = 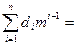d_im^i-1 + d_i-1m^i-2 +...+ d₂m¹ + d₁m⁰, (12.10)

где d_i – значение символа в соответствующем разряде, принимающее величину от 1 до n (для десятичной системы 10 знаков, для двоичной – два знака).

При использовании десятичной системы счисления для образования кода требуется десять различных импульсов, например отличающихся амплитудой, длительностью и т.д. Такое представление в теории связи применяют редко, поскольку для образования и его распознавания требуется сложная аппаратура. Наиболее просты арифметические действия в двоичной системе, имеющей всего два состояния единица и нуль. Двоичная система широко применяется при кодировании дискретных сообщений благодаря своей простоте и компактности.

В процессе кодирования элементы сообщения преобразуются в соответствующие им числа (кодовые символы). Каждый элемент записывается определенной совокупностью кодовых символов, которая называется кодовой комбинацией. Совокупность кодовых комбинаций, отражающих дискретные сообщения, представляет собой код. Правила кодирования приводят обычно в виде таблицы, где приводится алфавит кодируемых сообщений и соответствующие им кодовые комбинации. Множество возможных кодовых символов называется кодовым алфавитом, а их количество m – основанием кода.

По длине кодов и взаимному расположению в них символов различают равномерные и неравномерные коды.

Равномерные коды имеют одинаковую длину комбинаций. Для равномерного кода число возможных комбинаций составляет mⁿ. Примером такого кода является пятизначный код Бодо, применяемый в телеграфии. Код Бодо содержит пять двоичных элементов ( m = 2, n = 5). Число возможных кодовых комбинаций в этом коде равно 2⁵ = 32, что позволяет кодировать все буквы русского алфавита (твердый знак не передают). Однако этого мало для передачи сообщения на русском языке, содержащего буквы, цифры, знаки препинания и условные знаки (точка, запятая, двоеточие, сложение, вычитание и т.д.). Поэтому применяют «Международный код №2» (МТК-2). В коде МТК-2 используется регистровый принцип, согласно которому одна и та же пятиэлементная кодовая комбинация может использоваться до трех раз в зависимости от положения регистра: русский, латинский, цифровой. Общее число различных знаков при этом равно 84.

Для передачи по каналам связи данных рекомендован семиэлементный код МТК-5. Коды МТК-2 и МТК-5 являются первичными (простыми). Применение равномерных кодов упрощает построение буквопечатающих устройств и не требует передачи разделительных символов между кодовыми комбинациями.

Неравномерные коды отличаются тем, что кодовые комбинации у них отличаются друг от друга не только взаимным расположением символов, но и их количеством при минимизации средней длины кодовой последовательности. Однако проблема заключается в том, что у неравномерного кода на приемной стороне оказываются неизвестными границы этих комбинаций. Однозначное декодирование будет обеспечено, если ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие этим условиям, называются префиксными или неприводимыми. Наиболее известным неравномерным кодом является код Морзе, в котором символы 1 и 0 используются в двух сочетаниях, но код Морзе – это кодирование не с двоичным входным алфавитом (точка и тире), а с троичным: точка, тире, пробел.

По признаку помехозащищенности коды, как и методы кодирования, делят на примитивные (первичные, простые, безызбыточные) и помехоустойчивые (корректирующие, избыточные).

Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются примитивными. В простых равномерных кодах превращение одного символа комбинации в другой, например 0 в 1 или 1 в 0, приводит к появлению новой разрешенной комбинации, т.е. к ошибке в принятом сообщении.

В помехоустойчивых кодах для передачи сообщения используются не все кодовые комбинации, а только некоторая их часть (разрешенные кодовые комбинации). Тем самым создается возможность обнаружения и исправления ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов обеспечиваются введением в кодовые комбинации дополнительных (избыточных) символов. Помехоустойчивое кодирование используется в различных системах связи, при хранении и передаче данных, в компьютерных сетях, в бытовой и профессиональной аудио- видеотехнике, использующей цифровую запись.

Особое место занимает экономное кодирование, или сжатие данных, которое используют для повышения скорости передачи информации и приближения ее к пропускной способности канала. Экономное кодирование применяют в компьютерах для архивации информации.

Если экономное кодирование сокращает избыточность источника сообщений, то помехоустойчивое кодирование, наоборот, заключается в целенаправленном введении избыточности (дополнительных символов) для того, чтобы появилась возможность обнаруживать и (или) исправлять ошибки, возникающие при передаче по каналу связи.

Приведенная классификация не является исчерпывающей. В нее включены лишь некоторые коды и методы кодирования, которые широко используются в современных системах связи.