Основы синтеза цифровых фильтров

Разработка и практическое применение цифровых фильтров стали возможным во многом благодаря теории линейных аналоговых фильтров. Основные успехи были достигнуты при использовании некоторых важных соответствий между характеристиками цифровых и аналоговых фильтров. Задача синтеза цифрового фильтра состоит в определении системной (передаточной) функции и расчете параметров цифрового фильтра, эквивалентного аналоговому прототипу, и разработке на основе полученных данных алгоритма фильтрации. Цель синтеза цифрового фильтра заключается в том, чтобы цифровой тракт (аналогово-цифровой преобразователь и цифровой фильтр вырабатывал для заданного класса входных сигналов u(t) последовательность выходных отсчетов у_Т(t)=у_k, с гарантированной точностью совпадающих с дискретными значениями выходного сигнала гипотетического аналогового фильтра-прототипа у(t).

Желаемые характеристики цифрового фильтра, задаваемые обычно в виде дробно-рациональной системной (передаточной) функции или частотных и временн'ых характеристик, представляют исходные данные для задачи синтеза. Передаточную функцию аналогового фильтра можно записать

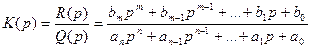(10.16)

Аргумент р представляет собой оператор дифференцирования р = d/dt, а самапередаточная функция определяет дифференциальное уравнение аналогового фильтра, которое можно представить в следующем виде:

(10.17)

где u(t) и у(t)—входнойи выходной аналоговый сигналы.

Итак, для синтеза цифровых фильтров необходимо осуществить прежде всего дифференцирование системной функции. Однако дифференцировать можно только непрерывные функции, а для дискретных числовых последовательностей операция дифференцирования не определена. Следовательно, цифровые фильтры не могут иметь математическую модель в виде дифференциального уравнения. Смысл практически всех методов синтеза цифровых фильтров сводится к замене операции дифференцирования некоторым дискретным ее эквивалентом. Таким образом, при синтезе выбирается гипотетический фильтр, называемый аналоговым прототипом синтезируемого цифрового фильтра.

10.8. Метод инвариантности импульсных характеристик

Данный метод основан на инвариантности (подобии, или неизменности) импульсной характеристики аналогового фильтра (фильтра-прототипа) и получения из нее путем дискретизации импульсной характеристики цифрового фильтра (рис. 10.14). Учитывая, что синтезируется физически реализуемая цепь, для которой импульсная характеристика равна нулю при t < 0, запишем выражение для импульсной характеристики цифрового фильтра

{h_k} = h(0), h(Δt), h(2Δt), ... = h₀, h₁, h₂, ... . (10.18)

°

Анализируемый метод синтеза цифрового фильтра осуществляется путем применения прямого z-преобразования к импульсной характеристике {h_k} вида (10.17) и вычисления системной функции H(z). Затем системную функцию фильтра H(z) сравнивают с общими выражениями (10.4) или (10.6) и определяют коэффициенты а_m и b_n соответственно нерекурсивной и рекурсивной части алгоритма фильтрации.

ПРИМЕР 10.8. Синтезировать нерекурсивный цифровой фильтр, основанный на дискретизации импульсной характеристики простейшего аналогового фильтра, подобный интегрирующей RC-цепи и имеющий заданную импульсную характеристику (рис. 10.14, а, б) (здесь принято для упрощения, что множитель 1/τ =1/RC) в импульсной характеристике равен единице)

0, t < 0;

h(t)= (10.19)

e^-Δt/τа, t ≥ 0.

Чтобы синтезировать нерекурсивный фильтр, ограничим число отсчетов его импульсной характеристики до трех:

{h_k} = 1, e^-Δt/τа, e^-2Δt/τа (10.20)

Системную функцию цифрового фильтра определим, применив

z-преобразование (10.2) к этой последовательности . Тогда

H(z) = 1 + e^-Δt/τа z^-1 + e^-2Δt/τа z^-2 (10.21)

Cравнив выражения (10.4) и (10.21), находим, что системная функция определяет структуру цифрового нерекурсивного фильтра второго порядка.

Заменив в (10.18) z = e ^jωΔt, запишем частотный коэффициент передачи

K_Ц (ω) = 1 + e^-Δt/τа e ^jωΔt + e^-2Δt/τа e ^j2ωΔt ..................(10.22)

Синтезируем рекурсивный цифровой фильтр для случая, когда импульсная характеристика (10.19) представляется бесконечной дискретной последовательностью отсчетов:

{h_k} = 1, e^-Δt/τа, e^-2Δt/τа, e^-3Δt/τа , ... . (10.23)

Выполнив z-преобразование данной импульсной характеристики, найдем системную функцию фильтра:

H(z) = 1 + e^-Δt/τа z^-1 + e^-2Δt/τа z^-2 +...=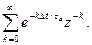

По аналогии с (10.2) эту формулу запишем в следующем виде:

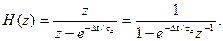(10.24)

Таким образом, функция (10.24) определяет рекурсивный фильтр 1-го порядка. Из этого соотношения путем подстановки z = e ^jωΔt находим частотный коэффициент передачи фильтра

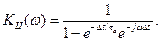(10.25)

Есть другие методы синтеза цифровых фильтров, в частности метод инвариантности частотных характеристик и дискретизации дифференциального уравнения аналоговой цепи.