Согласованный линейный фильтр

Прием радиосигналов всегда сопровождался помехами. Поэтому на протяжении всего развития радиотехники (в частности приемных устройств) центральной проблемой была и остается борьба с помехами и шумами (далее просто шумами). В случаях, когда мощность полезного сигнала соизмерима со средней мощностью шума, трудно не только выделить, но и обнаружить сигнал.

Основой большинства практических методов выделения сигнала из аддитивной смеси сигнала и шума в радиоприемных устройствах является оптимальная линейная фильтрация, использующая линейные частотные фильтры.

В теории приемных устройств установлено, что критерий качества линейной фильтрации зависит от одной из решаемых задач: обнаружение сигнала в шумах или разрешение сигналов. При обнаружении сигнала в шумах наиболее эффективен критерий максимума отношения сигнал/шум по мощности на выходе фильтра. Линейный фильтр, для которого это отношение максимально, называют оптимальным (наилучшим). Следует ожидать, что при подаче на вход оптимального фильтра аддитивной суммы полезного сигнала и шума на его выходе можно получить заметное увеличение отношения сигнал/шум.

Одним из основных параметров фильтров приемника является коэффициент передачи.

Коэффициент передачи оптимального фильтра приемника определим при условии. что сигнал принимается на фоне белого шума с двухсторонней спектральной плотностью мощности W₀ (напомним, что часто белый шум задается односторонней, т.е. в области физических частот спектральной плотностью мощности N₀ = 2W₀ ).

Для удобства анализа представим коэффициент передачи оптимального фильтра в виде

K 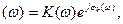(11.1)

где K(ω) – АЧХ; φ_k(ω) – ФЧХ фильтра.

Пусть входной сигнал u(t) имеет спектральную плотность

S(ω) = S(ω)e ^jφc(ω). (11.2)

Здесь S(ω) и φ_с(ω)—соответственно амплитудный и фазовый спектры принимаемого сигнала.

Отметим некоторый, пока неизвестный, момент времени t = t₀, при котором отношение сигнал/шум на выходе фильтра будет максимальным. В соответствии с известной формулой сигнал на выходе фильтра как линейного четырехполюсника равен

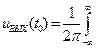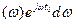S(ω)K (11.3)

Поскольку S_ВЫХ(ω) = S_ВХ(ω)К(ω), то можно найти среднюю мощность (дисперсию) белого шума на выходе фильтра:

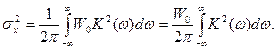(11.4)

Используя выражения (11.3) и (11.4), запишем отношение выходных мощностей сигнала и шума

(11.5)

Для удобства вычислений введем эквивалентный коэффициент передачи фильтра

K_э(ω) = К(ω) e ^jωt0 = 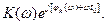(11.6)

Оптимальный коэффициент передачи анализируемого фильтра максимизирует правую часть выражения (11.5). Задача нахождения оптимального коэффициента передачи К(ω) решается на основе известного в математике неравенства Буняковского-Коши-Шварца, которое для данного случая имеет вид

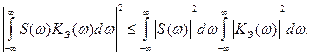(11.7)

Прямая подстановка показывает, что неравенство обращается в равенство, если

K_э(ω) = АS*(ω), (11.8)

где А – произвольный постоянный коэффициент; S*(ω) – функция комплексно-сопряженная с S(ω).

Представим эквивалентный коэффициент передачи (11.8) в виде:

K_э(ω) = К(ω)е ^jωt0 = АS*(ω) = AS(ω) .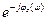

Отсюда находим коэффициент передачи фильтра

К(ω) = АS*( ω) е ^jωt0 = АS(ω) 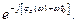(11.9)

Формула (11.9) полностью определяет коэффициент передачи оптимального фильтра, максимизирующего отношение сигнал/шум. Отсюда же следуют требования к АЧХ и ФЧХ оптимального фильтра

К(ω) = АS(ω), (11.10)

φ_к(ω) = − [φ_c(ω) + ωt₀]. (11.11)

По определению частотный коэффициент передачи – безразмерная величина, поэтому постоянный коэффициент А должен иметь размерность обратную размерности амплитудного спектра входного сигнала S(ω).

Сущность метода обработки принимаемого сигнала оптимальным фильтром приемника иллюстрируется рис. 11.1, где соответственно показаны и обозначены: спектр входного сигнала S(ω) и белого шума W₀; спектр выходного сигнала S_ВЫХ(ω) и АЧХ фильтра К(ω); энергетический спектр σ²_x(ω).

Эти результаты имеют следующий физический смысл. Формула (11.10) устанавливает, что АЧХ фильтра К(ω) должна с точностью до масштабного множителя А совпадать по форме с амплитудным спектром S(ω) входного сигнала. Благодаря этому, подавляющая часть спектральных составляющих входного сигнала, имеющих наибольшие амплитуды, проходит на выход оптимального фильтра практически без ослабления и вносит основной вклад в образование его пикового значения. Из множества же спектральных компонентов входного белого шума, располагающихся в бесконечной полосе частот, на выход фильтра проходят и не ослабляются только те, которые находятся под кривой его АЧХ, т.е. в ограниченной полосе частот..

гармонических составляющих спектра сигнала. Согласно этому условию, оптимальный фильтр должен иметь такую ФЧХ,

чтобы получаемый в нем фазовый сдвиг каждой гармоники − φ_c(ω) был равен по величине и противоположен по знаку начальной фазе соответствующей спектральной плотности S(ω) входного сигнала. Оптимальный фильтр проводит компенсацию («обнуление») начальных фаз всех спектральных составляющих сигнала u(t), в результате чего образуется и пик выходного сигнала. Составляющая ФЧХ - ωt₀ указывает на то, что пик (максимум) выходного сигнала задержан относительно начала действия входного сигнала на время t_0. Связь между фазовой характеристикой φ_c(ω) входного сигнала, компенсирующей ее фазовый характеристикой -φ_c(ω) и ФЧХ фильтра поясняется рис. 11.2. Фазовая характеристика выходного сигнала, определяемая формулой

φ_ВЫХ(ω) = φ_c(ω) + φ_k(ω) = φ_c(ω) + [−φ_c(ω) − ω t₀] = − ω t₀ (11.12)

показана на этом рисунке прямой линией.

Таким образом, коэффициент передачи фильтра, описываемый соотношением (11.1), согласован с амплитудным и фазовым (или фазовой характеристикой) спектрами входного сигнала. Поэтому такой фильтр часто называют согласованным.

Если вернуться к выражению (11.5), можно рассмотреть энергетические соотношения между сигналом и шумом на выходе оптимального фильтра. Поскольку квадрат модуля комплексного числа равен квадрату его действительной части, то, после несложных преобразований упомянутой формулы, получим:

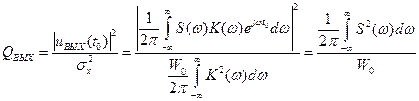. (11.13)

Числитель в формуле (8.16) в соответствии с равенством Парсеваля представляет собой энергию входного сигнала Э. Тогда последнее соотношение примет вид:

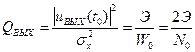. (11.14)

Согласно выражению (11.14), оптимальный фильтр обеспечивает максимум отношения сигнал/шум, которое зависит только от энергии входного сигнала и спектральной плотности мощности белого шума и совершенно не связано с формой входного сигнала.

ПРИМЕР 11.1 Полезный сигнал, поступающий на вход оптимального фильтра, представляет собой прямоугольный видеоимпульс с некоторой амплитудой Е и длительностью τ_И = 10 мкс. Белый шум на входе фильтра имеет спектральную плотность мощности W₀ = 25 ·10^-18 В²/Гц. Определить минимальное значение амплитуды Е, при которой возможно обнаружение сигнала, если приемник регистрирует его присутствие при отношении сигнал/шум Q_ВЫХ = Э/W₀ = 2 дБ (в практических схемах надежная регистрация осуществляется при Q_ВЫХ ≥ 13 дБ).

Р е ш е н и е . Требуемую величину отношения сигнал/шум найдем из условия 10 lq (Э/W₀) = 2, откуда Э/W₀ = 1,58. Поскольку энергия прямоугольного импульса Э = Е² τ_И, то

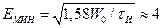мкВ.