Рекурсивные цифровые фильтры

Возможности нерекурсивного цифрового фильтра существенно расширяются при введении в его схему обратных связей, которые позволяют формировать k-й выходной отсчет путем использования предыдущих значений как входного, так и выходного дискретных (выраженных в цифровой форме) сигналов

y_k = a₀u_k + a₁u_k-1 + a₂u_k-2 + ...+ a_mu_k-m + b₁ y_k-1+ b₂ y_k-2+...+ b_n y_k-n (10.6)

Здесь коэффициенты а₀, а₁, а₂,..., а_m, как и в(10.1), характеризуют нерекурсивную часть, а коэффициенты b₁, b₂, ..., b_n – рекурсивную часть алгоритма цифровой фильтрации, причем последние не равны нулю одновременно. Порядок такого цифрового фильтра определяется коэффициентом m нерекурсивной части алгоритма обработки. Структурная схема цифрового рекурсивного фильтра показана на рис. 10.6.

Системную функцию рекурсивного фильтра определим, применив z-преобразование к обеим частям выражения (10.2).

. (10.7)

Пример 10.2. Вычислить импульсную характеристику рекурсивного цифрового фильтра, описываемого разностным уравнением 1-го порядка

h_k = 0.5y_k-1+ u_k

Р е ш е н и е. Пусть y_-1 = 0, u_k = δ_k (первое равенство очевидно в силу условия физической реализуемости; второе – сигнал на входе при определении импульсной характеристики). Тогда выходной сигнал фильтра y_k представляет его импульсную характеристику h_k, или y_k = h_k = 0,5 h_k + δ_k. Здесь δ_k = 1; 0; 0, ... . Из этих выражений следует, что

h₀ = 0.5h_-1 + δ₀ = 1; h₁ = 0,5 h₀ + δ₁ = 0,5; h₂ = 0,5 h₁ = 0.25. Если иначе

h_k = (0,5)^k.

Основное достоинство рекурсивных фильтров – существенное сокращение числа элементов по сравнению с их числом в нерекурсивных фильтрах, выполняющих те же операции. Это позволяет реализовать цифровые фильтры с импульсными характеристиками, имеющими теоретически бесконечное число отсчетов (рис. 10.3, б). Поэтому в радиотехнике рекурсивные цифровые фильтры получили название фильтров с бесконечными импульсными характеристиками (БИХ-фильтров).

ПРИМЕР 10.3. Построить цифровой фильтр, соответствующий аналоговой цепи в виде колебательного контура, имеющему импульсную характеристику

h(t) = e^-atcosω₀t

Р е ш е н и е. Импульсная характеристика цифрового фильтра будет представлена следующим образом

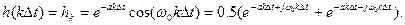
Системная функция, соответствующая этой импульсной характеристике такова:

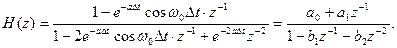
Здесь а₀ = 1, а₁=е^-а∆tcosω₀∆t, b₁= 2 е^-а∆tcosω₀∆t, b₂=- е^-2а∆t.

Данной системной функции отвечает уравнение:

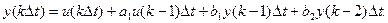
Схема рекурсивного фильтра, соответствующего этому алгоритму, показана на рис.10.7

10.5. Канонические схемы рекурсивных фильтров.

Недостаток рекурсивных фильтров, реализуемых по алгоритму (10.6), -- достаточно большое количество ячеек памяти, применяемых для рекурсивной и нерекурсивной частей. Уменьшить число ячеек позволяют канонические (в смысле оптимальности реализации) схемы рекурсивных фильтров, в которых каждый элемент задержки используется для цепей как нерекурсивной, так и рекурсивной связей. В канонических схемах количество элементов задержки всегда равно наибольшему из числа m и n.

Цифровой рекурсивный фильтр, соответствующий алгоритму обработки дискретного сигнала типа (10.7) может быть реализован в виде другой, эквивалентной схемы. Уравнение (10.7) можно представить иначе:

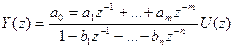(10.8)

Представим формулу (10.8) как:

, ....................................(10.9)

где 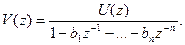(10.10)

Алгоритм (10.8) определяет структуру построения нерекурсивного фильтра m –го порядка. Преобразование, соответствующее функции V(z) и заданное (10.9), осуществляется с помощью рекурсивного фильтра n-го порядка. Итак, общая схема рекурсивного фильтра включает в себя две части – нерекурсивную с коэффициентами а_m и рекурсивную с коэффициентами b_n (Рис. 10.8). Дублирующие элементы схемы на рисунке. 10.8 можно

объединить. Полученную схему фильтра называют канонической (рис. 10.9).

ПРИМЕР 10.4. Составить структурную схему канонического рекурсивного фильтров 2-го порядка, описываемого системной функцией вида

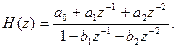
Р е ш е н и е. Схема изображена на рис. 10.10.