Частотные характеристики цифровых фильтров

Одним из важных показателей цифровых фильтров является частотный коэффициент передачи. Определение частотного коэффициента передачи цифрового фильтра становится простым, если условно входной сигнал представить в виде дискретной гармоники единичной амплитуды (Рис.10.11).

Используя формулу дискретной свертки (10.1), запишем m-й отсчет выходного сигнала цифрового фильтра в таком виде:

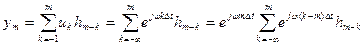(10.12)

Просуммируем члены ряда по новому индексу n = m – k:

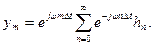(10.13)

Из выражения (10.13) следует, что выходной сигнал цифрового фильтра имеет структуру дискретной гармонической последовательности с частотой колебаний, равной частоте входного сигнала ω.

Определим частотный коэффициент передачи цифрового фильтра. Поделив (10.13) и (10.11), находим комплексный частотный коэффициент передачи фильтра:

(10.14)

Это соотношение позволяет сделать два очень важных вывода:

1. Частотный коэффициент передачи цифрового фильтра К_Ц(ω), как и спектр дискретного сигнала S_т(ω) [cм.(9.12)], имеет периодическую структуру с периодом по оси частот, равным частоте дискретизации ω₁ = 2π/Δt. Это фундаментальное положение для цифровых фильтров. Периодическая структура частотного коэффициента передачи цифрового фильтра позволяет либо выделить, либо подавить отдельные составляющие спектра дискретного входного сигнала.

2. Функция К_u(ω) является дискретным преобразование Фурье импульсной характеристики цифрового фильтра, аналитически представленной в виде последовательности дельта-функций:

h_Δ(t) = h₀δ(t)+ h₁δ(t- Δt)+ h₂δ(t-2 Δt)+... .

Для получения частотного коэффициента передачи, сравнив (10.2) и (10.14), достаточно в выражении для системной функции сделать подстановку z = e^jωΔt.

К_ц(ω) = H(e^jωΔt). (10.15)

Итак, системная функция, как и частотный коэффициент передачи имеет периодическую структуру с периодом по оси частот, равным частоте дискретизации ω₁ = 2π/Δt.

ПРИМЕР 10.5. Алгоритм нерекурсивной цифровой фильтрации имеет следующий вид у_к = 10u_k + 5u_k-1+ 2u_k-2. Найти импульсную характеристику, системную функцию и частотный коэффициент передачи цифрового фильтра.

Р е ш е н и е. С помощью (10.1), (10.2) и (10.14) найдем соответственно h_k, H(z) и К_Ц(ω)

1. Импульсная характериcтика {h_k} = (10, 5, 2).

2. Cистемная функция H(z) = 10 + 5z^-1 + 2z^-2.

3. Частотный коэффициент передачи можно найти, заменив в выражении для H(z) переменную z = e^jωΔt

K_ц(ω) = 10 + 5е^-jωt + 2 е^-jωt.

Используя формулу Эйлера, окончательно запишем

K_ц(ω) = 10 + 5cosω Δt + 2cos2ω Δt – j(5sin ω Δt +2sin2ω Δt).

ПРИМЕР 10.6. Рассчитать и построить АЧХ цифрового фильтра, структурная схема которого показана на рис. 10.12, а для значений ω Δt = 0^°, 90^°, 180^°, 270^°, 360^°.

Р е ш е н и е . Алгоритм работы этого фильтра – у_к = u_k - u_k-1. Находим z- преобразование выходных отсчетов фильтра

.

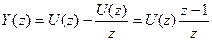Тогда системная функция фильтра

Заменив z = e^jωΔt, находим частотный коэффициент передачи:

K_ц(ω) = 1 – e^jωΔt = 1 – cosωΔt +j sinωΔt.

Как и в линейных аналоговых фильтрах, модуль частотного коэффициента передачи представляет АЧХ цифрового фильтра:

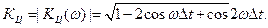
График АЧХ, построенный в соответствии с этой формулой, представлен на рис. 10.12, б, где по оси абсцисс отложен фазовый угол ω Δt.

ПРИМЕР 10.7. Нерекурсивный цифровой фильтр второго порядка работает в соответствии с алгоритмом

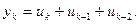
Определить и построить частотную характеристику цифрового фильтра. Проанализировать работу заданного фильтра при прохождении через него дискретной гармоники вида u_k = cos(ωkΔt) = e^jωkΔt имеющей интервал дискретизации Δt=π/(3ω).

Р е ш е н и е. Из алгоритма работы фильтра следует, что импульсная характеристика {h_k} = 1, 1, 1. Тогда системная функция фильтра

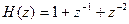
Заменив z = e^jωΔt, находим частотный коэффициент передачи

Как и в линейных аналоговых фильтрах, модуль частотного коэффициента передачи представляет АЧХ цифрового фильтра

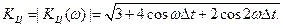
Построенный согласно этому выражению график АЧХ показан на рис. 10.13 а, где по оси абсцисс отложен фазовый угол ω Δt, величина которого соответствует интервалу дискретизации при текущем значении частоты. Заметим, одному заданному интервалу дискретизации Δt соответствуетфазовый угол ω Δt= 60°.

Фазочастотная характеристика фильтра определяется согласно известной формулы

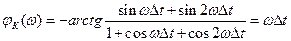
и имеет линейный вид.

Пусть на вход данного фильтра подается дискретная гармоника (рис. 10.13, б). В этом случае цифровая входная последовательность будет иметь вид:

...,0,1,1,0,-1,-1,0,1,1,0,...

В соответствии с заданным алгоритмом выходной сигнал фильтра определится следующей последовательностью

...,2, 2, 0, -2, -2, 0, 2, 2, ...

Как следует из значений выходной последовательности отсчетов, ей отвечает дискретная гармоника той же частоты, что и на входе. Амплитуда выходной гармоники равна удвоенной амплитуде входной гармоники, а начальная фаза смещена на 60° (т.е. на фазовый угол одного интервала дискретизации) в сторону запаздывания (рис. 10.13, в).