Закон сохранения энергии в механике
Рассмотрим систему из n материальных точек, на которые действуют как консервативные так и неконсервативные силы. Найдем работу, которую совершают эти силы при перемещении системы из одной конфигурации в другую. Работа консервативных сил может быть представлена как убыль потенциальной энергии системы 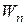 [(см. 4.8)]:
[(см. 4.8)]:
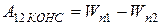 .
.
Работу неконсервативных сил обозначим посредством А*. Согласно (4) суммарная работа всех сил затрачивается на приращение кинетической энергии системы 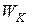 , следовательно,
, следовательно, 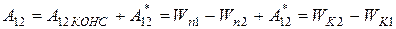 или
или
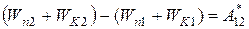 .
.
Сумма кинетической и потенциальной энергии представляет собой полную механическую энергию Е системы:
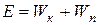 . (5)
. (5)
Таким образом
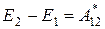 . (6)
. (6)
Очевидно, что если неконсервативные силы в системе отсутствуют, т.е. 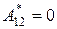 , то ее полная механическая энергия остается постоянной (сохраняется) т.е. Е = const. Эту теорему называют законом сохранения механической энергии, он утверждает: полная механическая энергия системы материальных точек, находящихся под действием консервативных сил остается постоянной.
, то ее полная механическая энергия остается постоянной (сохраняется) т.е. Е = const. Эту теорему называют законом сохранения механической энергии, он утверждает: полная механическая энергия системы материальных точек, находящихся под действием консервативных сил остается постоянной.
В такой системе могут происходить лишь превращения потенциальной энергии в кинетическую и обратно, но полный запас энергии системы измениться не может. При наличии неконсервативных сил (например, сил трения, сил сопротивления...) механическая энергия системы не сохраняется, она уменьшается, что приводит к ее нагреванию. Такой процесс называется диссипацией (рассеянием) энергии. Силы, приводящие к диссипации энергии, называются диссипативными.
Дата добавления: 2016-09-26; просмотров: 1592;











