Закон движения дается векторным уравнением
Л Е К Ц И Я № 1. К И Н Е М А Т И К А
Кинематика – это раздел механики, в котором изучается движение тел без рассмотрения причин, вызывающих движение.
Движением тела называют изменение его положения относительно другого тела в пространстве с течением времени.
Тела, относительно которых рассматривается изучаемое движение, называются телами отсчета (например, стены лаборатории, Земля...).
Обычно с этими телами связывают систему координат. Мы будем пользоваться правой прямоугольной системой координат X, Y, Z.
Системой отсчета называется система координат, снабженная часами и жестко связанная с абсолютно твердым телом.
Абсолютно твердым телом называется тело, расстояние между любыми двумя точками которого всегда остается неизменным.
Кинематика материальной точки. Путь, перемещение, скорость и ускорение
|
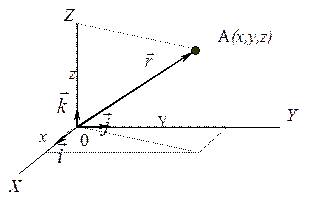 Изучение законов движения естественно начать с изучениядвижения тела, размерами которого можно пренебречь. Такое тело называют материальной точкой. Движение материальной точки по отношению к системе отсчета может быть задано векторным или координатным способами.
Изучение законов движения естественно начать с изучениядвижения тела, размерами которого можно пренебречь. Такое тело называют материальной точкой. Движение материальной точки по отношению к системе отсчета может быть задано векторным или координатным способами.
При векторном способе положение точки А, рис. 1, в момент времени t определяется ее радиусом вектором 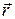 , проведенным из начала координат до движущейся точки.
, проведенным из начала координат до движущейся точки.
Закон движения дается векторным уравнением
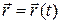 . (1)
. (1)
При координатном способе положение точки А определяется координатами x, y, z, а закон движения задается тремя уравнениями:
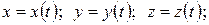 (2)
(2)
при этом 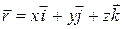 , (3)
, (3)
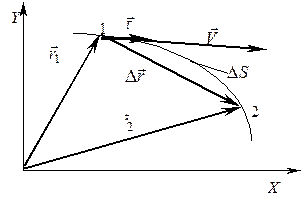 где
где 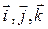 – единичные по модулю и взаимно перпендикулярные векторы-орты системы координат.
– единичные по модулю и взаимно перпендикулярные векторы-орты системы координат.
|
|
 Непрерывная линия, которую описывает точка при своем движении, называется траекторией. На рисунке 2 показана траектория точки. В зависимости от формы траектории различают прямолинейное движение и криволинейное движение (частный случай – движение по окружности ).
Непрерывная линия, которую описывает точка при своем движении, называется траекторией. На рисунке 2 показана траектория точки. В зависимости от формы траектории различают прямолинейное движение и криволинейное движение (частный случай – движение по окружности ).
|
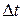 точка пройдет путь
точка пройдет путь 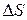 .
.
Перемещение точки за промежуток времени 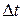 – вектор
– вектор 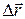 , соединяющий положении точки в моменты t и t +
, соединяющий положении точки в моменты t и t + 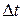 . Из рис. 2 видно, что вектор перемещения
. Из рис. 2 видно, что вектор перемещения
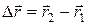 . (4)
. (4)
Скорость
Мгновенная скорость материальной точки определяется соотношением

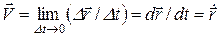 , (5)
, (5)
т.е. мгновенная скорость есть производная радиуса-вектора по времени. Она направлена по касательной к траектории движущейся точки.
В физике принято производные по времени обозначать не штрихом, а (×) над буквой.
Из рис. 2 видно, что при 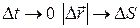 , поэтому модуль скорости
, поэтому модуль скорости
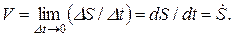 (6)
(6)
Можно описать движение через параметры траектории. Для этого некоторую точку на траектории примем за начальную, тогда любая другая точка характеризуется расстоянием S(t) от нее. Радиус вектор становится сложной функцией вида 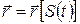 , поэтому из (5) следует:
, поэтому из (5) следует:
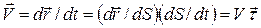 ,
,
где
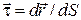 – единичный вектор, касательный к траектории;
– единичный вектор, касательный к траектории; 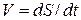 – модуль скорости.
– модуль скорости.
В СИ скорость измеряется в метрах в секунду (м/с).
С учетом формулы (3) из (5) получаем
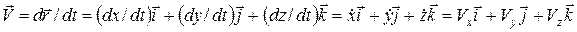 , (7)
, (7)
где
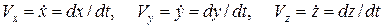 (8)
(8)
– компоненты скорости, они равны производным соответствующих координат по времени.
На рис. 2, 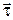 обозначает единичный касательный вектор, он совпадает с направлением скорости
обозначает единичный касательный вектор, он совпадает с направлением скорости 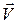 , поэтому
, поэтому
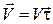 . (9)
. (9)
1.1.2. Ускорение
Для характеристики быстроты изменения скорости вводится векторная физическая величина, называемая ускорением 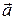 . Она определяется аналогично скорости:
. Она определяется аналогично скорости:
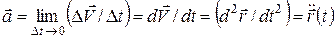 . (10)
. (10)
С учетом формул (7) и (8) из (10) находим
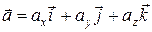 (11)
(11)
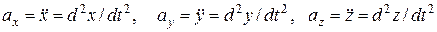 (12)
(12)
– компоненты ускорения, они равны вторым производным соответствующих координат по времени.
С учетом формулы (9) из (10) получаем
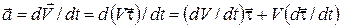 . (13)
. (13)
Можно показать, что
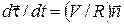 , (14)
, (14)
где R – радиус кривизны в данной точке траектории, а 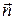 – единичный вектор нормали к траектории в точке, в которой было тело в момент времени t. При этом
– единичный вектор нормали к траектории в точке, в которой было тело в момент времени t. При этом 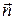 и
и 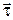 взаимноперпендикулярны (см. рис. 3).
взаимноперпендикулярны (см. рис. 3).
Каждой точке кривой можно сопоставить окружность, которая сливается с траекторией на бесконечно малом ее участке. Радиус этой окружности R., (см. рис. 3), характеризует кривизну линии в рассматриваемой точке и называется радиусом кривизны.
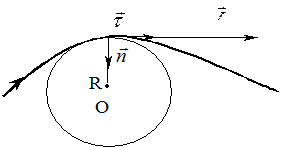 Подставляя (14) в (13), получа
Подставляя (14) в (13), получа 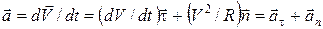 , (15)
, (15)
где
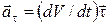 , (16)
, (16)
|
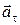 – касательное или тангенциальное ускорение. По величине оно характеризует быстроту изменения модуля скорости:
– касательное или тангенциальное ускорение. По величине оно характеризует быстроту изменения модуля скорости:
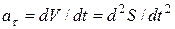 . (17)
. (17)
При ускоренном движении 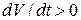 и
и 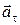 совпадает по направлению со скоростью
совпадает по направлению со скоростью 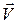 , при замедленном движении
, при замедленном движении 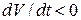 и
и 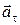 противоположно скорости
противоположно скорости 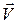 . Второе слагаемое в (15)
. Второе слагаемое в (15)
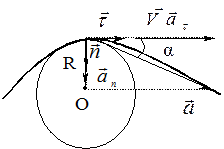
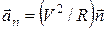 (18)
(18)
|
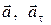 и
и 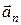 для случая ускоренного движения.
для случая ускоренного движения.
Модуль ускорения точки 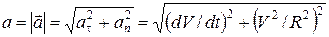 . (19)
. (19)
Ускорение измеряется в метрах на секунду в квадрате (м/с2).
Дата добавления: 2016-09-26; просмотров: 2920;











