Реактивное движение. Движение тел с переменной массой
Имеется много явлений, в основе которых лежит закон сохранения импульса. Например, полет ракет (и работа реактивных двигателей) основаны на том, что в результате выбрасывания из сопла газов, ракете сообщается такой жеимпульс, который уносят с собой газы. Впервые мысль о возможности такого применения реактивных двигателей была высказана Кибальчичем в 1881 г. Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты.
Пусть m(t) – масса ракеты в произвольный момент времени t, 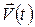 – ее скорость в тот жемомент времени, а
– ее скорость в тот жемомент времени, а 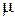 – скорость убыли ее массы [m = (dm/dt)]за счет истечения газов. Импульс ракеты в этот момент будет
– скорость убыли ее массы [m = (dm/dt)]за счет истечения газов. Импульс ракеты в этот момент будет 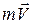 . В следующий момент времени (t+dt) ракета будет иметь массу
. В следующий момент времени (t+dt) ракета будет иметь массу 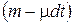 , а ее скорость получит приращение
, а ее скорость получит приращение 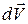 и будет равна
и будет равна 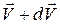 . Отделившиеся от ракеты газы будут иметь относительно Земли скорость
. Отделившиеся от ракеты газы будут иметь относительно Земли скорость 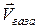 . Тогда импульс ракеты в момент времени (t+dt) равен:
. Тогда импульс ракеты в момент времени (t+dt) равен: 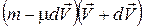 , импульс газов
, импульс газов 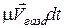 . Изменение импульса всей системы (ракета + ее газы) за время dt будет равно:
. Изменение импульса всей системы (ракета + ее газы) за время dt будет равно:
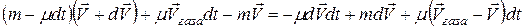 (13)
(13)
В уравнении (13), 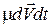 как членом второго порядка малости можно пренебречь. Согласно второму закону Ньютона скорость изменения импульса за время dt равна внешней силе, действующей на это тело за это время, т. е.:
как членом второго порядка малости можно пренебречь. Согласно второму закону Ньютона скорость изменения импульса за время dt равна внешней силе, действующей на это тело за это время, т. е.: 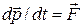 . С учетом (13) находим
. С учетом (13) находим
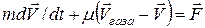 (14)
(14)
или 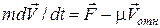 , (15)
, (15)
где 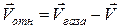 – скорость истечения газов относительно ракеты. Уравнение (15) называют уравнением Мещерского или уравнением движения точки с переменной массой. Если
– скорость истечения газов относительно ракеты. Уравнение (15) называют уравнением Мещерского или уравнением движения точки с переменной массой. Если 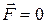 , то уравнение (15) переходит в уравнение вида:
, то уравнение (15) переходит в уравнение вида:
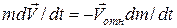 , (16)
, (16)
решая которое можно получить:
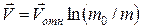 , (17)
, (17)
где т0 - начальная стартовая масса ракеты (когда 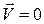 ) .
) .
Максимальная скорость
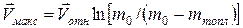 , (18)
, (18)
где ттопл – масса топлива и окислителя. В действительности, скорость будет меньше. Формула (17) называется Формулой Ц и о л к о в с к о г о.
Дата добавления: 2016-09-26; просмотров: 2011;











