Выходной сигнал фильтра определяется следующим соотношением

.

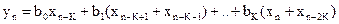Выразим Z – преобразование выходного сигнала фильтра через Z – преобразование входного сигнала

.

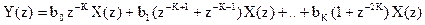Разделив Y(z) на X(z), найдем системную функцию

.

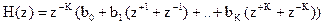Найдем комплексный коэффициент передачи фильтра, используя подстановку .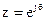

.

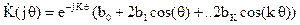Обозначим

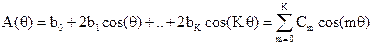, (2.26)

где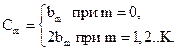

Тогда АЧХ и ФЧХ (без приведения в интервал от -π до π) фильтра определятся следующими соотношениями

,

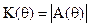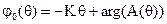. (2.27)

Так как второе слагаемое в выражении для ФЧХ - константа (0 или π), ФЧХ этого фильтра является линейно-ломаной.

Линейность ФЧХ обусловлена симметрией коэффициентов системной функции относительно середины линии задержки (симметрией импульсной характеристики фильтра).

2.10. Устойчивость цифровых фильтров

Рассмотрим критерии устойчивости цифровых фильтров.

1.Критерий «ОВ-ОВ» («Ограниченный вход – ограниченный выход»)

Цифровой фильтр устойчив, если при ограниченном входном сигнале выходной сигнал фильтра также ограничен.

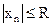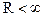Условие ограниченности входного сигнала определяется соотношением , где , а условием ограниченности выходного сигнала является .

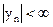Непосредственное использование этого критерия весьма затруднительно, т.к. требует определения значений отсчетов выходного сигнала при всех возможных значениях отсчетов входного сигнала. Поэтому требуются критерии, позволяющие оценить устойчивость фильтра на основании его характеристик.

2. Критерий оценки устойчивости по импульсной характеристике фильтра

В разделе 2.3 было доказано, что выходной сигнал фильтра представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра

.

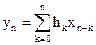Абсолютное значения отсчетов выходного сигнала удовлетворяет неравенству

.

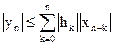При 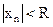справедливо неравенство

.

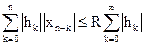Следовательно,

.

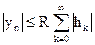Таким образом, чтобы обеспечить выполнение условия 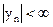, достаточно выполнить условие

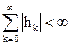. (2.28)

Последнее соотношение определяет критерий устойчивости цифрового фильтра, который формулируется так: цифровой фильтр устойчив, если сумма абсолютных значений отсчетов его импульсной характеристики конечна.

Из этого критерия следует, что все фильтры с конечной импульсной характеристикой абсолютно устойчивы.

В качестве примера воспользуемся критерием (2.28) для проверки устойчивости фильтра, импульсная характеристика которого бесконечна и описывается соотношением

,

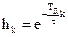где 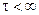– положительная константа, от которой зависит скорость убывания отсчетов импульсной характеристики.

Учитывая, что 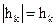, получим

.

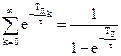Так как 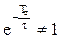, то фильтр устойчив.

3. Критерий оценки устойчивости по системной функции фильтра

В разделе 2.4 показано, что системная функция представляет собой Z-преобразование импульсной характеристики фильтра

.

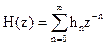Модуль системной функции удовлетворяет неравенству

.

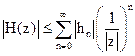При 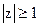справедливо неравенство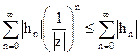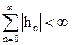

.

При и при 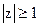модуль системной функции 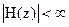. Последнее соотношение означает, что в устойчивом цифровом фильтре должны отсутствовать полюсы системной функции в области комплексной переменной z, которая удовлетворяет неравенству .

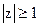Следовательно, если полюсы существуют, то в устойчивом фильтре они должны располагаться в области комплексной плоскости, для которой выполняется условие .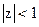

Поэтому критерий устойчивости, связанный с системной функцией фильтра, формулируется следующим образом: цифровой фильтр устойчив, если полюсы системной функции располагаются внутри круга единичного радиуса с центром в начале координат ( ).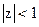

Оценим устойчивость фильтра, системная функция которого описывается соотношением

,

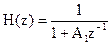где A₁= - 0.5.

Приравняем знаменатель системной функции нулю и определим корень полученного уравнения, который является координатой полюса

.

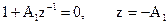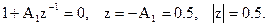
Так как 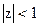, то полюс системной функции располагается внутри круга единичного радиуса. Следовательно, фильтр устойчив.

2.11. Коэффициенты системной функции устойчивого звена

второго порядка

Системная функция звена второго порядка определяется соотношением

.

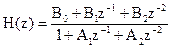Для определения полюсов системной функции приравняем знаменатель нулю и найдем корни полученного квадратного уравнения

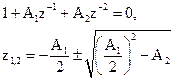
Фильтр реализуется в виде звеньев второго порядка в случае комплексно-сопряженных корней, т.е. при

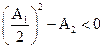. (2.29)

В этом случае корни уравнения определяются следующим соотношением

.

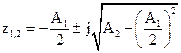Из последнего соотношения находим

.

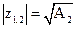Условием устойчивости звена является

.

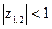Поэтому коэффициент A₂ устойчивого звена второго порядка должен удовлетворять условию

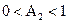. (2.30)

Из неравенств (2.29) и (3.30) следует неравенство для коэффициента A₁

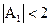. (2.31)

Заключение

Математическим аппаратом цифровой фильтрации является Z – преобразование. Знание трех основных свойств Z – преобразования (линейности, теоремы о задержки и о дискретной свертке) позволяет решать задачи анализа фильтра при известной схеме фильтра – графическом представлении алгоритма цифровой фильтрации.

Основные этапы анализа:

1. Выражение выходного сигнала фильтра через входной сигнал – запись разностного уравнения;

2. Выражение Z-преобразования выходного сигнала через Z – преобразование входного сигнала фильтра,

3. Определение системной функции фильтра ;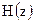

4. Определение зависимости комплексного коэффициента передачи фильтра от частоты 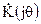путем использования подстановки в выражение системной функции

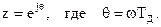
5. Определение АЧХ фильтра

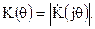
6. Определение ФЧХ фильтра

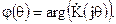
7. Определение импульсной характеристики фильтра путем нахождения обратного Z – преобразования системной функции фильтра.

Контрольные вопросы по теме №2:

1. Что такое импульсная характеристика цифрового фильтра?
2. На рисунке 2.40 показаны входной сигнал фильтра x_n и его импульсная характеристика h_n. Начертите временную диаграмму выходного сигнала фильтра y_n.

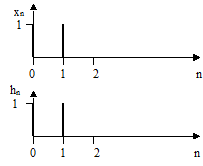
Рисунок 2.40

3. Определите 4 отсчета импульсной характеристики h₀, h₁, h₂, h₃ цифрового фильтра рисунка 2.41, где A = -0.5

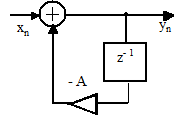
Рисунок 2.41

4. Что называется системной функцией цифрового фильтра?

5. Определите системную функцию цифрового фильтра рисунка 2.41.

6. Какая связь существует между импульсной характеристикой и системной функцией цифрового фильтра?

7. Выразите Z-преобразование выходного сигнала цифрового фильтра рисунка 2.42 через Z –преобразование входного сигнала

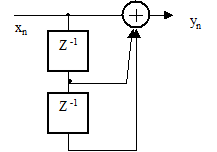
Рисунок 2.42

8. Выразите Z-преобразование выходного сигнала линии задержки рисунка 2.43 через Z-преобразование входного сигнала.

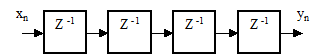
Рисунок 2.43

9. Выразите Z-преобразование выходного сигнала фильтра рисунка 2.44 через Z-преобразование входного сигнала.

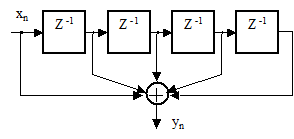
Рисунок 2.44

10. На входе фильтра действует сигнал x_n, а на выходе сигнал y_n. Временные диаграммы этих сигналов приведены на рисунке 2.45. Определите системную функцию фильтра.

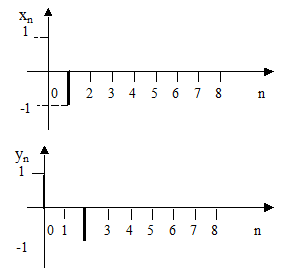
Рисунок 2.45

11. Системная функция цифрового фильтра определяется соотношением

.

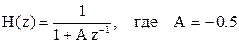Чему равен полюс системной функции фильтра?

12. На рисунке 2.46 приведена импульсная характеристика цифрового фильтра. Какова системная функция фильтра?

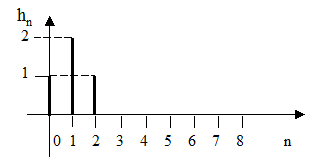
Рисунок 2.46

13. Какова системная функция цифрового фильтра рисунка 2.47

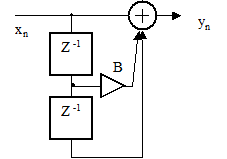
Рисунок 2.47

14. Системная функция цифрового фильтра определяется соотношением

.

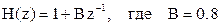Чему равен нуль системной функции фильтра?

15. На входе фильтра (рисунок 2.48) действует сигнал x_n (рисунок 2.49). Каков выходной сигнал фильтра при нулевых начальных условиях?

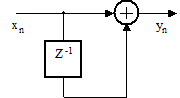
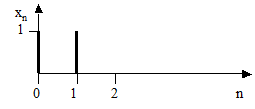
Рисунок 2.48 Рисунок 2.49

16. На рисунке 2.50 приведена импульсная характеристика цифрового фильтра. Выразите Z-преобразование выходного сигнала фильтра через Z-преобразование входного сигнала

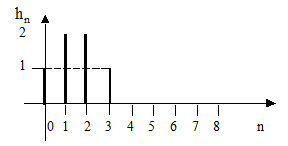
Рисунок 2.50

17. Каков коэффициент передачи фильтра (рисунок 2.51) на частоте, равной четверти частоты дискретизации?

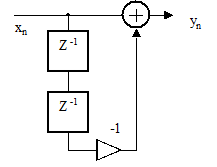
Рисунок 2.51

18. Системная функция цифрового фильтра определяется соотношением

.

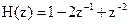Чему равен коэффициент передачи фильтра на частоте f=0?

19. На входе цифровой линии задержки (рисунок 2.52) действует синусоидальный сигнал x_n , частота которого равна одной восьмой частоты дискретизации. Чему равен фазовый сдвиг выходного сигнала y_n относительно входного сигнал?

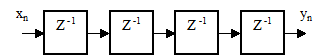
Рисунок 2.52

20. Какой из двух цифровых фильтров рисунка 2.53 обладает линейной ФЧХ?

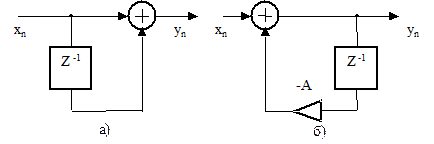
Рисунок 2.53

21. Системная функция цифрового фильтра определяется соотношением

.

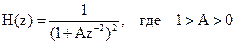Чему равен фазовый сдвиг, вносимый фильтром на частоте, равной четверти частоты дискретизации?

22. На входе цифровой цепи рисунка 2.54 действует синусоидальный сигнал с амплитудой, равной единице. Чему равна амплитуда выходного сигнала?

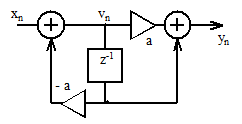
Рисунок 2.54

23. Системная функция цифрового фильтра описывается соотношением

.

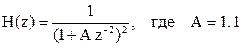Сделайте вывод об устойчивости фильтра.

24 . Сделайте вывод об устойчивости фильтра рисунка 2.55 при A1₁= -0.5, A1₂= - 1.9.

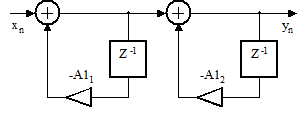
Рисунок 2.55

25. На рисунке 2.56 приведена импульсная характеристика цифрового фильтра. Сделайте заключение об устойчивости фильтра

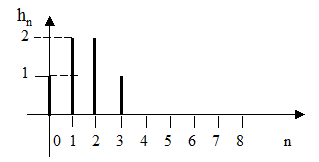
Рисунок 2.56

26. Системная функция цифрового фильтра описывается соотношением

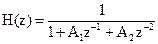, где A₁ = 0.1, А₂ =0.9

Сделайте вывод об устойчивости фильтра.

27. Системная функция цифрового фильтра определяется соотношением

.

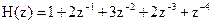Сделайте вывод об устойчивости фильтра.

Контрольная карта ответов

Номер ответа соответствует номеру контрольного вопроса в предыдущем разделе.

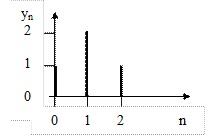
2.

3. y₀ = 1.000, y₁= 0.500, y₂ = 0.250, y₃ = 0.125.

5.

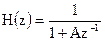
7.

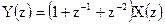
8.

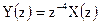
9.

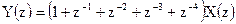
10.

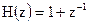
11. z_п = 0.5

12.

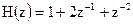
13.

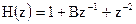
14. z₀ = - 0.8

15. y₀ = 1, y₁ = 2, y₂ =1

16.

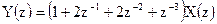
17. K=2

18. K=0

19.

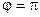
20. Рисунок 2.53 а

21.

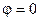
22. Амплитуда выходного сигнала Y=1

23. Не устойчив

24. Не устойчив

25. Устойчив

26. Устойчив

27. Устойчив

Список литературы по теме №2:

1. В.Г.Иванова, А.И.Тяжев. Цифровая обработка сигналов и сигнальные процессоры / Под редакцией д.т.н., профессора Тяжева А.И. - Самара, 2008г.

2.Куприянов М.С., Матюшкин Б.Д. Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. –2-е изд., перераб. и доп.- СПб.: Политехника, 1999. –592с.:ил.

3.А.Б. Сергиенко. Цифровая обработка сигналов. – СПб.: Питер, 2002.-2002.-608с.:ил.

4.А.И. Солонина, Д.А. Улахович, С.М. Арбузов, Е.Б. Соловьёва. Основы цифровой обработки сигналов.- Изд. 2-е испр. И перераб. – СПб.: БХВ-Петербург, 2005.-768с.: ил.

5.Л. Рабинер, Б. Гоулд. Теория и применение цифровой обработки сигналов.- Издательство «Мир», 1978. –848с.,ил.

6.В. Каппелини, А.Дж.Константинидис, П.Эмилиани. Цифровые фильтры и их применение.- М.:Энергоатомиздат, 1983-360с.:ил.

7.Р.В. Хемминг. Цифровые фильтры. – М.: Сов. Радио, 1980-224с., ил.