Выходной сигнал детектора определяется следующим соотношением

w_n = (-1) ^m( x _n-1 x _n-K+1 - x _n x_n-K ).

Для нахождения детекторной характеристики найдем w _n при x _n= X₀ cos(wnT_Д).

В результате получим

w = (-1) ^m X₀ ² sin(wT_Д) sin(w(K-1) T_Д ).

При w = w₀ + Dw и w₀T_Д = p/2 получим

w = X₀ ² sin(Dw(K-1)T_Д) cos(DwT_Д) = X₀ ² sin(2pDf(K-1)/F_Д) cos(2pDf/F_Д).

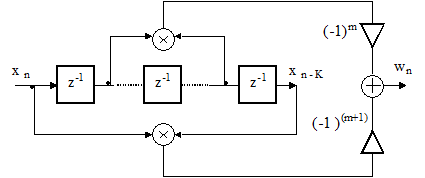
Рисунок 3.31 – Частотной детектор на цифровой линии задержки

Введем нормированное отклонение частоты Df_N = Df/F_Д. Тогда детекторная характеристика может быть представлена следующим образом

w(Df_N) = X₀² sin(2pDf_N(K-1)) cos(2pDf_N).

На рисунке 3.32 приведены детекторные характеристики при X=1, K=3 (w₁(Df_N)) и при K=5 (w₂(Df_N)).

Из него видно, что с увеличением K увеличивается крутизна рабочего участка детекторной характеристики, но уменьшается ее раствор, т.е. частотный интервал между двумя экстремальными точками характеристики, ближайшими к Df_N= 0.

Коэффициенты второй и третьей гармоник выходного сигнала детектора равны

, .

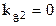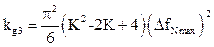Сравнивая последние соотношения с аналогичными выражениями для автокорреляционного частотного детектора, можно сделать вывод о том, что коэффициент третьей гармоники выходного сигнала детектора на цифровой линии задержки в 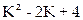раз больше коэффициента третьей гармоники сигнала на выходе автокорреляционного детектора. Причем с увеличением длины линии задержки искажения увеличиваются. Такой вывод можно сделать и из сравнения детекторных характеристик рисунка 3.33 с детекторной характеристикой рисунке 3.29. Это является недостатком данного детектора. Его достоинство - простота.

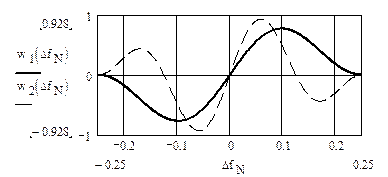
Рисунок 3.32 – Детекторные характеристики частотного детектора

на цифровой линии задержки при K=3 и K=5

Заключение

В идеальном 90-градусном ФР составляющие спектра одинаковой частоты двух выходных сигналов имеют равные амплитуды и сдвинуты по фазе на 90 градусов.

В реальном нерекурсивном 90 – градусном ФР отсутствует фазовая погрешность, однако АЧХ ФР по выходам косинусной и синусной компонент отличаются друг от друга. Следовательно, этот ФР вносит амплитудную погрешность, которую можно уменьшить за счет увеличения длины линии задержки и оптимального выбора коэффициентов системной функции ФР по выходу синусной компоненты.

Реальный рекурсивный 90 – градусной ФР реализуется на всепропускающих цифровых цепочках первого порядка, поэтому он не вносит амплитудной погрешности, но имеет фазовую погрешность, которая уменьшается при увеличении количества этих цепочек.

Цифровые генераторы прямоугольных, треугольных, трапециедальных и синусоидальных колебаний строятся на базе генератора пилообразного колебания.

Частота пилы прямо пропорциональна частоте дискретизации, константе А, определяющей шаг изменения отсчета пилы за интервал дискретизации, и обратно пропорционален константе P, определяющей размах пилообразного колебания.

Цифровые преобразователи частоты реализуются на основе операции перемножения отсчета входного сигнала на отсчет вспомогательного синусоидального колебания. Выделение полезного продукта преобразования частоты осуществляется или с помощью цифрового фильтра, или фазокомпенсационным способом в квадратурных преобразователях частоты, для реализации которых используются 90 – градусные фазорасщепители и косинусно-синусные генераторы.

В разделе «Амплитудные детекторы» рассмотрены два нелинейных детектора (детектор – выпрямитель и детектор с блоком извлечения квадратного корня) и два синхронных детектора (синхронный амплитудный детектор с управляемым косинусно-синусным генератором и синхронный детектор с узкополосным фильтром для выделения несущей).

Наиболее простым в программной реализации является детектор – выпрямитель, но его применение ограничено частотой несущей входного сигнала, меньшей одной восьмой частоты дискретизации из - за зависимости выходного сигнала от начальной фазы несущей.

Наиболее сложным является синхронный детектор с управляемым косинусно-синусным генератором, но он не накладывает ограничения на частоту несущей входного сигнала и обеспечивает минимальные нелилейные искажения выходного сигнала.

В разделе «Фазовые детекторы» рассмотрены детектор с выходным ФНЧ, квадратурный детектор и квадратурный детектор с пилообразной детекторной характеристикой.

Эти детекторы работают по принципу преобразования частоты, когда частота опорного колебания равна частоте входного сигнала.

Детекторной характеристикой первых двух детекторов является косинусоида. Достоинством третьего является наличие линейных участков детекторной характеристики, а значит, отсутствие нелинейных искажений выходного сигнала детектора.

В разделе «Частотные детекторы» рассмотрены автокорреляционный частотный детектор с выходным ФНЧ, квадратурный автокорреляционный частотный детектор, квадратурный автокорреляционный частотный детектор с внутренним амплитудным ограничением, частотный детектор на цифровой линии задержки, синхронно-фазовый частотный детектор.

Наиболее простыми в реализации являются автокорреляционный детектора с выходным ФНЧ и детектор на цифровой линии задержки. Недостатком этих детекторов являются относительно большие нелинейные искажения выходного сигнала. Из-за больших нелинейных искажений детектор на цифровой линии задержки используют при детектировании сигнала частотной манипуляции.

Наиболее сложной является реализация автокорреляционного детектора с внутренним амплитудным ограничением и синхронно-фазового частотного детектора. Их достоинство – линейная детекторная характеристика. Кроме того детектор с внутренним амплитудным ограничением обеспечивает независимость выходного сигнала от амплитуды сигнала на входе детектора.

Контрольные вопросы по теме №3:

1. На входе цифровой цепи рисунка 3.36 действует синусоидальный сигнал 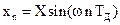. Запишите аналитическое выражение выходного сигнала y_n в случае идеального нерекурсивного 90 - градусного фазорасщепителя (ФР). Как изменится y_n при наличии амплитудной погрешности фазорасщепителя?

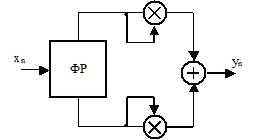
Рисунок 3.36

2. Каким образом можно уменьшить амплитудную погрешность нерекурсивного 90 – градусного фазорасщепителя?

3. На входе цифровой цепи рисунка 3.36 действует синусоидальный сигнал 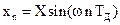. Запишите аналитическое выражение выходного сигнала y_n в случае идеального рекурсивного 90 - градусного фазорасщепителя (ФР). Как изменится y_n при наличии фазовой погрешности фазорасщепителя?

4. Каким образом можно уменьшить фазовую погрешность рекурсивного 90 – градусного фазорасщепителя?

5. На входе всепропускающей цифровой цепи рисунка 3.4 действует синусоидальный сигнал с амплитудой X=1. Чему равна амплитуда выходного сигнала?

6.Пилообразное колебание формируется в соответствии с соотношением

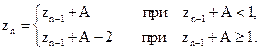
Запишите аналитическое выражение для пилообразного колебания 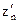, опережающего 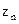на треть периода.

7. На рисунке 3.12 показано формирование трапецеидального колебания из треугольного. Как влияет константа B на форму трапеции?

8. В чем преимущество и недостаток использования полинома пятой степени по сравнению с полиномом третьей степени при формировании синусоидального колебания методом полиномиальной аппроксимации?

9. Что нужно изменить в преобразователе частоты рисунка 3.16, чтобы вместо колебания с частотой ω -ω_Г на выходе преобразователя получить колебание с частотой ω +ω_Г ?

10.Каково назначение амплитудного детектора?

11. Почему амплитудный детектор – выпрямитель не следует применять на частоте несущей, равной четверти частоты дискретизации?

12. Сформулируйте достоинства и основной недостаток амплитудного детектора с блоком извлечения квадратного корня.

13. Поясните принцип работы синхронного амплитудного детектора с управляемым косинусно-синусным генератором.

14. Поясните принцип работы синхронного амплитудного детектора с узкополосным фильтром для выделения несущей. К чему приводит ненулевой коэффициент передачи узкополосного фильтра на боковых частотах амплитудно-модулированного сигнала?

15. Каково назначение фазового детектора?

16. Дайте определение детекторной характеристике фазового детектора. Какой математической функцией описываются детекторные характеристики фазового детектора с выходным ФНЧ и квадратурного фазового детектора?

17. Каково назначение частотного детектора?

18. Дайте определение детекторной характеристике частотного детектора.

19. Частота сигнала на входе автокорреляционного частотного детектора изменяется по закону 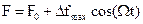, где F₀=F_Д/4 – частота несущей, приведенная в интервал Котельникова, 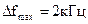, F_Д=20 кГц. Детекторная характеристика детектора приведена на рисунке 3.29. Чему равна амплитуда выходного сигнала детектора?

20. Сформулируйте достоинства и основной недостаток квадратурного автокорреляционного частотного детектора с внутренним амплитудным ограничением.

21. Частота сигнала на входе частотного детектора на цифровой линии задержки изменяется по закону 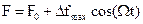, где F₀ = F_Д/4 – частота несущей, приведенная в интервал Котельникова, 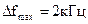, F_Д=20 кГц. Детекторные характеристики детектора при разной длине линии задержки приведены на рисунке 3.33. Чем отличаются по форме временные диаграммы выходного сигнала детектора при К = 3 и К = 5?

22. Поясните принцип работы синхронно-фазового частотного детектора.