Соотношение неопределенностей.
Согласно двойственной корпускулярно-волновой природе частиц вещества, для описания микрочастиц используются то волновые, то корпускулярные представления. Поэтому приписывать им все свойства частиц и все свойства волн нельзя. Естественно, что необходимо внести некоторые ограничения в применении к объектам микромира понятий классической механики.
В классической механике всякая частица движется по определенной траектории, так что в любой момент времени точно фиксированы ее координата и импульс. Микрочастицы из-за наличия у них волновых свойств существенно отличаются от классических частиц. Одно из основных различий заключается в том, что нельзя говорить о движении микрочастицы по определенной траектории и неправомерно говорить об одновременных точных значениях ее координаты и импульса. Это следует из корпускулярно-волнового дуализма. Так, понятие «длина волны в данной точке» лишено физического смысла, а поскольку импульс выражается через длину волны, то отсюда следует, что микрочастица с определенным импульсом имеет полностью неопределенную координату. И наоборот, если микрочастица находится в состоянии с точным значением координаты, то ее импульс является полностью неопределенным.
В. Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел в 1927 г. к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой, и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату, и определенную проекцию импульса, причем неопределенности этих величин удовлетворяют условиям:
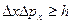 ,
, 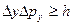 ,
, 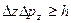 (2.4)
(2.4)
Т.е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.
Из соотношения неопределенностей (2.4) следует, что, например, если микрочастица находится в состоянии с точным значением координаты ( 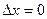 ), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной (
), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной ( 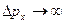 ), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактически невозможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта
), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактически невозможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта
Невозможность одновременно точно определить координату и соответствующую проекцию импульса не связана с несовершенством методов измерения или измерительных приборов, а является следствием специфики микрообъектов, отражающей особенности их объективных свойств, а именно двойственной корпускулярно-волновой природы. Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты и импульса) и наличия у нее волновых свойств. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.
Соотношение неопределенностей позволяет оценить, например, в какой мере можно применять понятия классической механики к микрочастицам, в частности, с какой степенью точности можно говорить о траекториях микрочастиц. Известно, что движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Выразим соотношение неопределенностей (2.4) в виде:
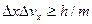 (2.5)
(2.5)
Из этого выражения следует, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости и, следовательно, с тем большей точностью можно применять к этой частице понятие траектории. Так, например, уже для пылинки массой 10-12 кг и линейными размерами 10-6 м, координата которой определена с точностью до 0,01 ее размеров ( 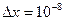 м), неопределенность скорости по (2.5)
м), неопределенность скорости по (2.5) 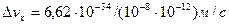 = 6,62×10-14 м/с, т. е. не будет сказываться при всех скоростях, с которыми пылинка может двигаться. Таким образом, для макроскопических тел их волновые свойства не играют никакой роли; координата и скорость макротел могут быть одновременно измерены достаточно точно. Это означает, что для описания движения макротел с абсолютной достоверностью можно пользоваться законами классической механики.
= 6,62×10-14 м/с, т. е. не будет сказываться при всех скоростях, с которыми пылинка может двигаться. Таким образом, для макроскопических тел их волновые свойства не играют никакой роли; координата и скорость макротел могут быть одновременно измерены достаточно точно. Это означает, что для описания движения макротел с абсолютной достоверностью можно пользоваться законами классической механики.
Предположим, пучок электронов движется вдоль оси x со скоростью v=108 м/с, определяемой с точностью до 0,01 % ( 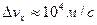 ). Какова точность определения координаты электрона? Оценим ее по формуле:
). Какова точность определения координаты электрона? Оценим ее по формуле:
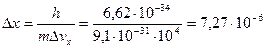 м,
м,
т.е. положение электрона может быть определено с точностью до тысячных долей миллиметра. Такая точность достаточна, чтобы можно было говорить о движении электронов по определенной траектории, иными словами, описывать их движение законами классической механики.
Применим соотношение неопределенностей к электрону, движущемуся в атоме водорода. Допустим, что неопределенность координаты электрона 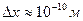 (порядка размеров самого атома). Тогда согласно (2.5),
(порядка размеров самого атома). Тогда согласно (2.5), 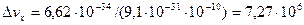 м/с. Используя законы классической физики, можно показать, что при движении электрона вокруг ядра по круговой орбите радиуса » 0,5×10-10 м его скорость v » 2,3×106 м/с. Таким образом, неопределенность скорости в несколько раз больше самой скорости. Очевидно, что в данном случае нельзя говорить о движении электрона в атоме по определенной траектории, иными словами, для описания движения электрона в атоме нельзя пользоваться законами классической физики.
м/с. Используя законы классической физики, можно показать, что при движении электрона вокруг ядра по круговой орбите радиуса » 0,5×10-10 м его скорость v » 2,3×106 м/с. Таким образом, неопределенность скорости в несколько раз больше самой скорости. Очевидно, что в данном случае нельзя говорить о движении электрона в атоме по определенной траектории, иными словами, для описания движения электрона в атоме нельзя пользоваться законами классической физики.
В квантовой теории рассматривается также соотношение неопределенностей для энергии E и времени t, т.е. неопределенности этих величин удовлетворяют условию:
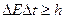 (2.6)
(2.6)
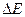 - неопределенность энергии некоторого состояния системы,
- неопределенность энергии некоторого состояния системы, 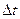 - промежуток времени, в течение которого оно существует. Следовательно, система, имеющая среднее время жизни
- промежуток времени, в течение которого оно существует. Следовательно, система, имеющая среднее время жизни 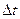 , не может быть охарактеризована определенным значением энергии; разброс энергии
, не может быть охарактеризована определенным значением энергии; разброс энергии 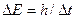 возрастает с уменьшением среднего времени жизни. Из выражения (2.6) следует, что частота излученного фотона также должна иметь неопределенность
возрастает с уменьшением среднего времени жизни. Из выражения (2.6) следует, что частота излученного фотона также должна иметь неопределенность 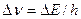 , т.е. линии спектра должны характеризоваться частотой, равной
, т.е. линии спектра должны характеризоваться частотой, равной 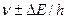 . Опыт действительно показывает, что все спектральные линии размыты; измеряя ширину спектральной линии, можно оценить порядок времени существования атома в возбужденном состоянии.
. Опыт действительно показывает, что все спектральные линии размыты; измеряя ширину спектральной линии, можно оценить порядок времени существования атома в возбужденном состоянии.
Дата добавления: 2020-12-11; просмотров: 517;











