Случайные события и их вероятности
Событие – любое явление, в отношении которого имеет смысл говорить, наступило оно или не наступило в результате определенного комплекса условий или случайного эксперимента. Отсюда следует, что событие можно рассматривать, как величину, которая может принимать только два значения.
Можно выделить виды событий.
Событие называется достоверным, если оно обязательно происходит при каждом осуществлении определенной совокупности условий. Например, если брошена игральная кость, то выпадение не менее одного и не более шести очков является достоверным событием.
Событие называется невозможным, если оно заведомо не произойдет ни при одном осуществлении данной совокупности условий. Например, если брошена игральная кость, то выпадение более шести очков является невозможным событием.
Событие называется случайным, если оно может произойти, а может и не произойти при осуществлении данной совокупности условий. Например, если брошена игральная кость, то выпадение любого из шести очков является случайным событием.
События называются несовместимыми, если их одновременное появление при осуществлении данной совокупности условий невозможно, т. е. появление события А в данном испытании исключает появление события В в этом же испытании. Например, если из урны с черными и белыми шарами случайным образом извлекается белый шар, то его появление исключает извлечение черного шара в той же попытке.
События называются единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием. Например, если стрелок произвел выстрел, то обязательно происходит одно из двух событий – попадание или промах. Эти события единственно возможные.
Совокупность единственно возможных событий испытания называется полной группой событий.
События называются равновозможными, если есть основания считать, что ни одно из этих событий не является более возможным, чем другие. Например, появление герба или решетки при бросании монеты есть события равновозможные.
Если 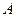 – какое либо событие, то событие, состоящее в том, что событие
– какое либо событие, то событие, состоящее в том, что событие 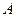 не наступило, называется событием противоположным событию
не наступило, называется событием противоположным событию 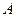 или отрицанием события
или отрицанием события 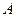 и обозначается
и обозначается 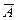 .
.
Суммой событий 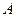 и
и 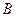 называется такое событие, обозначаемое
называется такое событие, обозначаемое 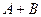 , которое происходит только тогда, когда происходит хотя бы одно из событий
, которое происходит только тогда, когда происходит хотя бы одно из событий 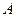 или
или 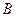 или оба вместе.
или оба вместе.
Произведением событий 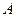 и
и 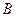 называется такое событие, обозначаемое
называется такое событие, обозначаемое 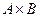 , которое происходит только тогда, когда происходят оба события
, которое происходит только тогда, когда происходят оба события 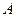 и
и 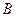 одновременно. Если
одновременно. Если 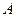 и
и 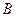 несовместимые события, то событие
несовместимые события, то событие 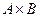 является невозможным.
является невозможным.
События, происходящие при реализации определенного комплекса условий или в результате случайного эксперимента, называются элементарными исходами. Считается, что при проведении случайного эксперимента реализуется только один из возможных элементарных исходов. Множество всех элементарных исходов случайного эксперимента называется пространством элементарных исходов.
Те элементарные исходы, при которых наступает интересующее нас событие, называются исходами, благоприятствующимиэтому событию.
Вероятностьсобытия 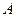 – это отношение числа благоприятствующих этому событию элементарных исходов к общему числу всех возможных и равновозможных элементарных исходов эксперимента
– это отношение числа благоприятствующих этому событию элементарных исходов к общему числу всех возможных и равновозможных элементарных исходов эксперимента 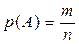 , где
, где 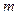 – число элементарных исходов, благоприятствующих событию
– число элементарных исходов, благоприятствующих событию 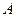 ;
; 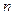 – число всех возможных элементарных исходов эксперимента.
– число всех возможных элементарных исходов эксперимента.
Можно определить следующие свойства вероятности:
– вероятность достоверного события равна 1;
– вероятность невозможного события равна 0;
– вероятность случайного события есть положительное число, заключенное между 0 и 1: 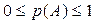 .
.
Математическое понятие вероятности случайного события является абстрактной характеристикой, присущей не самим интересующим нас объектам материального мира, а их теоретико-множественным моделям. Требуется некоторое дополнительное соглашение для того, чтобы можно было извлекать сведения о вероятностях из экспериментальных данных. В соответствии с классическим определением принято оценивать вероятность события относительной частотой благоприятных исходов опыта. Если проведено N независимых испытаний и в n из них наблюдалось событие 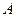 , то эмпирическая (выборочная) оценка вероятности
, то эмпирическая (выборочная) оценка вероятности 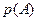 , которую можно получить из этой серии, равна:
, которую можно получить из этой серии, равна: 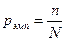 . При этом полагают, что
. При этом полагают, что 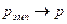 , если число испытаний
, если число испытаний 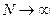 .
.
Основные теоремы теории вероятностей
1. Теорема сложения вероятностей. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий за вычетом вероятности их одновременного наступления
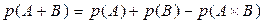 .
.
Если 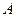 и
и 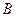 несовместимые события, то событие
несовместимые события, то событие 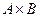 является невозможным. Следовательно,
является невозможным. Следовательно, 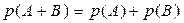 . Обобщая на несколько попарно несовместимых событий, можно записать
. Обобщая на несколько попарно несовместимых событий, можно записать 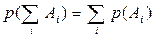 .
.
Если события 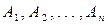 образуют полную группу, то сумма вероятностей этих событий равна единице:
образуют полную группу, то сумма вероятностей этих событий равна единице: 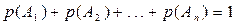 . Сумма вероятностей противоположных событий равна единице:
. Сумма вероятностей противоположных событий равна единице: 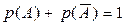 .
.
2. Теорема умножения вероятностей.Предположим, что из общего числа 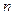 исходов испытания событию
исходов испытания событию 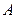 благоприятствуют
благоприятствуют 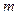 элементарных исходов, событию
элементарных исходов, событию 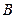 благоприятствуют
благоприятствуют 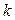 элементарных исходов, а одновременному наступлению событий
элементарных исходов, а одновременному наступлению событий 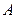 и
и 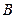 благоприятствуют
благоприятствуют 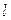 элементарных исходов. Если событие
элементарных исходов. Если событие 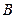 наступило, то это означает, что осуществился один из
наступило, то это означает, что осуществился один из 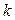 благоприятствующих ему исходов, причем из этих
благоприятствующих ему исходов, причем из этих 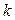 исходов благоприятствовать событию
исходов благоприятствовать событию 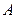 будут и те
будут и те 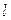 исходов, при которых события
исходов, при которых события 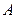 и
и 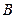 наступают одновременно. В связи с этим вводится понятие условной вероятности. Условной вероятностью
наступают одновременно. В связи с этим вводится понятие условной вероятности. Условной вероятностью 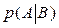 называют вероятность события
называют вероятность события 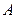 , вычисленную в предположении, что событие
, вычисленную в предположении, что событие 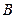 уже наступило. Независимыми событиями называются события, если вероятность одного из них не зависит от наступления или ненаступления другого. Если событие
уже наступило. Независимыми событиями называются события, если вероятность одного из них не зависит от наступления или ненаступления другого. Если событие 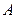 независимо от события
независимо от события 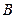 , то
, то 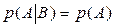 . События
. События 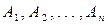 называются независимыми в совокупности, если каждое из этих событий независимо в паре с любым произведением остальных событий, содержащим как все остальные события, так и любую их часть. Независимость событий
называются независимыми в совокупности, если каждое из этих событий независимо в паре с любым произведением остальных событий, содержащим как все остальные события, так и любую их часть. Независимость событий 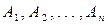 в совокупности влечет за собой попарную независимость этих событий. Для двух случайных зависимых событий вероятность произведения этих событий (т. е. одновременного появления в одном испытании) равна произведению вероятностей одного из них на условную вероятность другого, рассчитанную при условии, что первое событие уже произошло:
в совокупности влечет за собой попарную независимость этих событий. Для двух случайных зависимых событий вероятность произведения этих событий (т. е. одновременного появления в одном испытании) равна произведению вероятностей одного из них на условную вероятность другого, рассчитанную при условии, что первое событие уже произошло: 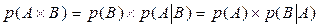 . Если событие
. Если событие 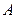 независимо от события
независимо от события 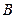 , то
, то 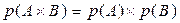 . Вероятность одновременного появления нескольких попарно независимых событий
. Вероятность одновременного появления нескольких попарно независимых событий 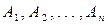 равна произведению их вероятностей:
равна произведению их вероятностей: 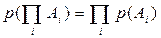 .
.
3. Теорема полной вероятности.Пусть имеется группа событий 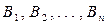 , обладающих следующими свойствами: а) все события попарно несовместимы; б) их объединение образует пространство элементарных исходов; в) они образуют полную группу событий. Такие события называют гипотезами, поскольку заранее неизвестно, какое из этих событий наступит. Пусть
, обладающих следующими свойствами: а) все события попарно несовместимы; б) их объединение образует пространство элементарных исходов; в) они образуют полную группу событий. Такие события называют гипотезами, поскольку заранее неизвестно, какое из этих событий наступит. Пусть 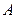 – некоторое событие, которое может произойти при наступлении одного и только одного из событий
– некоторое событие, которое может произойти при наступлении одного и только одного из событий 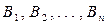 . Это означает, что
. Это означает, что 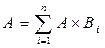 . Вероятность события
. Вероятность события 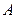 , которое может наступить лишь при условии появления одного из несовместимых событий
, которое может наступить лишь при условии появления одного из несовместимых событий 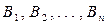 , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события
, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события 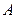 :
: 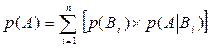 . Приведенная формула называется формулой полной вероятности.
. Приведенная формула называется формулой полной вероятности.
4. Формула Байеса.Пусть, как и в предыдущем случае имеем совокупность события 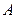 и группы событий
и группы событий 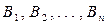 , обладающих теми же свойствами. Допустим, что событие
, обладающих теми же свойствами. Допустим, что событие 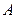 произошло и требуется определить, как в связи с этим изменились вероятности гипотез, т. е.
произошло и требуется определить, как в связи с этим изменились вероятности гипотез, т. е. 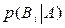 . Эта задача решается с помощью формулы Байеса
. Эта задача решается с помощью формулы Байеса 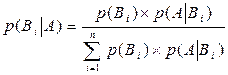 . Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие
. Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие 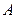 , т. е. найти апостериорные вероятности. Используя понятие условной вероятности формулу Байеса можно интерпретировать как вероятность того, что причиной появления события
, т. е. найти апостериорные вероятности. Используя понятие условной вероятности формулу Байеса можно интерпретировать как вероятность того, что причиной появления события 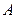 является событие
является событие 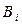 .
.
5. Формула Бернулли.Пусть производится 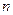 независимых испытаний, в каждом из которых событие
независимых испытаний, в каждом из которых событие 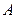 может появиться, либо не появиться. Будем считать, что вероятность события
может появиться, либо не появиться. Будем считать, что вероятность события 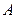 в каждом испытании одна и та же и равна
в каждом испытании одна и та же и равна 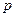 . Следовательно, вероятность ненаступления события
. Следовательно, вероятность ненаступления события 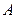 в каждом испытании также постоянна и равна
в каждом испытании также постоянна и равна 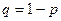 . Вероятность того, что при этих условиях при n испытаниях событие
. Вероятность того, что при этих условиях при n испытаниях событие 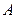 произойдет ровно k раз и, следовательно, не произойдет
произойдет ровно k раз и, следовательно, не произойдет 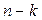 раз определяется по формуле Бернулли
раз определяется по формуле Бернулли 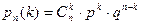 , где
, где 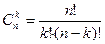 . Формулу Бернулли называют также формулой биномиального распределения вероятностей, поскольку в правой ее части стоит
. Формулу Бернулли называют также формулой биномиального распределения вероятностей, поскольку в правой ее части стоит 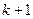 -й член бинома Ньютона.
-й член бинома Ньютона.
6. Локальная теорема Лапласа.При больших 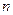 формулой Бернулли пользоваться затруднительно из-за громоздкости вычислений. Для этого случая доказана так называемая локальная теорема Лапласа, дающая асимптотическую формулу, которая позволяет приближенной найти вероятность появления события
формулой Бернулли пользоваться затруднительно из-за громоздкости вычислений. Для этого случая доказана так называемая локальная теорема Лапласа, дающая асимптотическую формулу, которая позволяет приближенной найти вероятность появления события 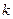 раз в
раз в 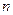 испытаниях, если число испытаний достаточно велико
испытаниях, если число испытаний достаточно велико 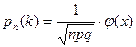 , где
, где 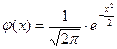 и
и 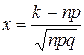 . Для функции
. Для функции 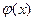 составлены таблицы, соответствующие положительным значениям аргумента
составлены таблицы, соответствующие положительным значениям аргумента 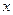 , поскольку
, поскольку 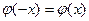 . Формула Лапласа дает тем большую точность, чем больше
. Формула Лапласа дает тем большую точность, чем больше 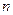 .
.
7. Интегральная теорема Лапласа.Если при тех же условиях, что и в предыдущем случае, требуется найти вероятность того, что событие 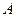 появится в
появится в 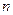 испытаниях не менее
испытаниях не менее 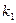 раз и не более
раз и не более 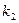 раз, то пользуются интегральной теоремой Лапласа
раз, то пользуются интегральной теоремой Лапласа 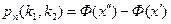 , где
, где 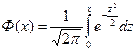 – табличная функция, называемая функцией Лапласа. Эта функция обладает следующими свойствами: а)
– табличная функция, называемая функцией Лапласа. Эта функция обладает следующими свойствами: а) 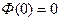 ; б)
; б) 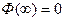 ; в)
; в) 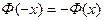 т. е. функция нечетна. Значения аргумента x находятся по формулам:
т. е. функция нечетна. Значения аргумента x находятся по формулам: 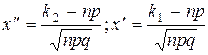 .
.
Основное отличие понятия вероятности от относительной частоты появления события состоит в том, что первую характеристику вычисляют до опыта, а вторую – после опыта. В том случае, если относительная частота наступления события обнаруживает устойчивую закономерность, т. е. если отношение 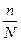 для достаточно больших
для достаточно больших 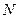 и большинства серий испытаний мало отклоняется от некоторой постоянной величины, то эту постоянную величину называют статистической вероятностью появления события. Для сопоставления этих величин также используется функция Лапласа. Пусть производится
и большинства серий испытаний мало отклоняется от некоторой постоянной величины, то эту постоянную величину называют статистической вероятностью появления события. Для сопоставления этих величин также используется функция Лапласа. Пусть производится 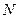 независимых испытаний, в каждом из которых событие
независимых испытаний, в каждом из которых событие 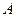 может появиться, либо не появиться. Будем считать, что вероятность события
может появиться, либо не появиться. Будем считать, что вероятность события 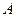 в каждом испытании одна и та же и равна
в каждом испытании одна и та же и равна 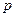 . Следовательно, вероятность ненаступления события
. Следовательно, вероятность ненаступления события 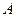 в каждом испытании также постоянна и равна
в каждом испытании также постоянна и равна 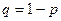 . Необходимо определить вероятность того, что отклонение относительной частоты
. Необходимо определить вероятность того, что отклонение относительной частоты 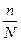 от вероятности
от вероятности 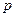 по абсолютной величине не превышает e>0. Это осуществляется с помощью следующей формулы
по абсолютной величине не превышает e>0. Это осуществляется с помощью следующей формулы 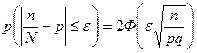 .
.
8. Формула Пуассона.При тех же условиях, что и в предыдущих случаях, но если 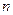 велико (
велико ( 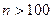 ), а
), а 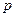 мало (
мало ( 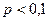 ), вместо локальной формулы Лапласа удобнее пользоваться асимптотической формулой Пуассона
), вместо локальной формулы Лапласа удобнее пользоваться асимптотической формулой Пуассона 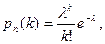 где
где 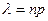 .
.
Дата добавления: 2016-09-06; просмотров: 7180;











