Глава 4. Спектральное описание случайных процессов

Для теории сигналов большое значение имеет разложение заданной функции f(x) по различным ортогональным системам функций j_n(x).

Бесконечная система функций j_n(x) называется ортогональной на отрезке [a, b], если 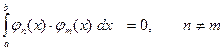. При этом предполагается, что 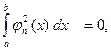т.е. что никакая из функций j_n(x) не равна тождественно нулю.

В математике доказывается, что если функции j_n(x) непрерывны, то произвольная абсолютно интегрируемая функция f(x) может быть представлена в виде ряда 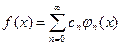, который называется обобщенным рядом Фурье по данной системе функций j_n(x).

Совокупность коэффициентов с_n называется спектром функции f(x) в ортогональной системе j_n(x). Применительно к сигналам s(t), которые являются функциями времени можно записать .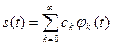

При разложении периодического сигнала s(t) в ряд Фурье в качестве ортогональной системы функций берут функции

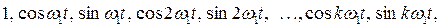
или

.

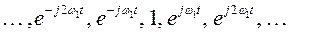Интервал ортогональности в обоих случаях совпадает с периодом T=2p/w₁ функции s(t).

Первая система функций приводит к тригонометрической форме ряда Фурье, вторая – к комплексной форме.

При использовании комплексной формы ряд Фурье записывается следующим образом .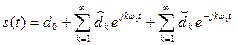

При такой записи ряда Фурье периодический сигнал заменяется суммой простых гармонических колебаний, как с положительными, так и с отрицательными частотами. Конечно, отрицательные частоты здесь не имеют физического смысла. Они появляются в результате применения символического метода расчета и анализа электрических цепей. Действительно, каждое слагаемое первого ряда можно представить в виде вектора на комплексной плоскости, который вращается против часовой стрелки с частотой kw₁. Каждое слагаемое второго ряда – вектор, вращающийся с той же частотой, но в противоположном направлении.

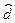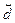Отрицательная частота - kw₁ только указывает направление вращения вектора. Так как и – комплексно сопряженные величины, то сумма векторов в любой момент времени дает вектор, направленный по вещественной оси, т. е k-ю гармоническую составляющую вещественной функции времени s(t).

При переходе к тригонометрической форме базисных функций понятие отрицательной частоты теряет смысл, и ряд Фурье записывается следующим образом .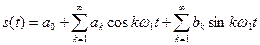

Чтобы разложить периодическую функцию в ряд. Фурье, нужно определить амплитуды и начальные фазы всех гармоник, а также постоянную составляющую. Аналитически разложение выполняется по формулам:

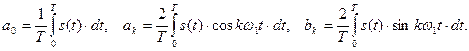
Совокупность коэффициентов ряда Фурье в базисе тригонометрических функций называется частотным спектром периодической функции.

Спектр периодической функции называется линейчатым или дискретным, так как состоит из отдельных линий, длина которых пропорциональна амплитудам (коэффициентам ряда) гармоник, имеющих дискретные частоты kw₁.

Пользуясь приведенными ранее выражениями, можно определить спектр периодической последовательности прямоугольных импульсов длительностью t с периодом T и амплитудой U.

Для этого сигнала 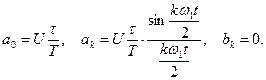Следовательно, сигнал можно представить рядом Фурье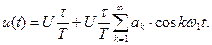

Анализ этого выражения показывает, что амплитуды спектральных составляющих убывают по закону 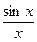, обращаясь в нуль на частотах, кратных скважности 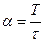последовательности.

Если предположить, что период последовательности прямоугольных импульсов T®µ , то получим спектр одиночного прямоугольного импульса, т.е. непериодического сигнала.

Математически спектр непериодической функции, определяется уже не рядом Фурье, а интегралом Фурье, он будет не дискретным, а сплошным, и называться спектральной плотностью .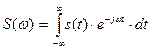

Полученное выражение, обеспечивающее переход от представления сигнала во временной области к его представлению в частотной области, называется прямым преобразованием Фурье. Если известно представление сигнала в частотной области 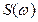, то можно найти его представление во временной области за счет использования обратного преобразования Фурье .

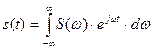Спектральная плотность одиночного прямоугольного импульса, вычисленная с помощью интеграла Фурье, имеет следующий вид: .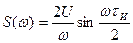

Из сопоставления закона изменения амплитуд гармонических составляющих дискретного спектра периодической последовательности прямоугольных импульсов и формы кривой спектральной плотности одиночного прямоугольного импульса можно сделать важный и общий для всех форм импульсов вывод. Дискретный спектр периодической последовательности импульсов вписывается в кривую спектральной плотности одиночного импульса этой же формы, которая называется огибающей дискретного спектра.

Если сигнал описывается функцией вида 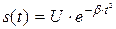, то он называется гауссовым импульсом. Такой сигнал лишь условно можно назвать импульсом из-за его поведения при t ®µ. Однако, условие b>0 обеспечивает достаточно быстрое уменьшение мгновенного значения сигнала с ростом времени. Поэтому применяют понятие эффективной длительности подобных импульсов, определяемое из условия десятикратного уменьшения уровня сигнала, т.е. t_и находится из условия 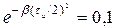. С учетом этого спектральная плотность гауссова импульса .

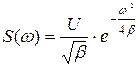Таким образом, спектральная плотность гауссова импульса вещественна и описывается гауссовой же функцией частоты.

Пусть сигнал s(t) представляет собой короткий импульс, сосредоточенный в точке t =0 и имеющий площадь А. Его математическая модель s(t) = А d(t), где d(t) – дельта–функция. Спектральная плотность этого сигнала 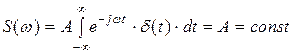, т. е. дельта–импульс имеет равномерный спектр на всех частотах.

Если ввести понятие ширины спектра детерминированного сигнала и понимать под ней частотный интервал, в пределах которого модуль спектральной плотности не меньше некоторого наперед заданного уровня, например (рис. 3),
Рис. 3. Ширина спектра

изменяется в пределах от |S|_max до 0,1|S|_max, то из рассмотренных примеров можно заключить, что 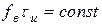, откуда следует важный вывод: чем меньше длительность импульса, тем шире его спектр.

Обобщая сказанное о спектральном представлении детерминированных процессов, можно сделать следующие выводы:

1. Спектральное представление детерминированного процесса представляет собой разложение его на сумму (конечную или бесконечную) элементарных гармонических процессов с различными частотами.

2. Периодические процессы представляются в виде рядов Фурье, которые образуются суммированием бесконечного числа гармоник с частотами, кратными основной частоте периодического процесса.

3. Спектральное представление непериодических, в частности импульсных, процессов осуществляется путем их разложения в интеграл Фурье.

4. В частотной области непериодический процесс характеризуется своей спектральной плотностью. Процесс и его спектр взаимно связаны парой прямого и обратного преобразований Фурье.

5. Для существования спектральной плотности в классическом смысле необходимо, чтобы функция, описывающая процесс, была абсолютно интегрируема.

6. Спектральная плотность неинтегрируемой функции содержит особенности типа дельта–функции.

Понятно, что применение преобразования Фурье непосредственно к случайному процессу невозможно. Однако его можно применить к конкретной реализации случайного процесса как неслучайной функции времени, а затем произвести усреднение по реализациям.

В соответствии с этим методом для каждой реализации x_i(t) случайного процесса X(t) находится спектральная функция .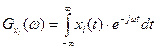

Затем может быть найдена средняя за время Т_р существования реализации мощность .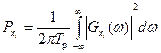

Функция, определяемая в соответствии с выражением 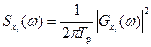, называется плотностью мощности по частоте или спектром мощности реализации. Она характеризует распределение энергии реализации по оси частот.

Усреднение этой функции по всем реализациям x_i(t) случайного процесса X(t) дает спектральную характеристику этого случайного процесса, называемую спектральной плотностью мощности или спектром мощности процесса

.

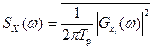Таким образом, случайный процесс во временной области порождает другой случайный процесс в частотной области, поскольку функции S_X(w) являются случайными функциями частоты.

Следует подчеркнуть различие между спектральной плотностью S(w) детерминированного процесса и спектральной плотностью мощности S_X(w) случайного процесса X(t). Первая характеризует меру энергии, приходящуюся на единичную полосу частот, а вторая – удельную меру мощности. Этот факт находит свое отражение и в разных физических размерностях этих величин.

По своему физическому смыслу спектр мощности веществен и неотрицателен, т. е. S_X(w)³0. В связи с этим целесообразно ввести понятие так называемого одностороннего спектра мощности N(w) случайного процесса, определяемого следующим образом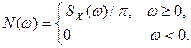

Вывод о стационарности случайного процесса, представленного спектром мощности S_X(w), можно сделать по виду этой функции. Для того, чтобы процесс был стационарен, любые два ее значения, отвечающие двум несовпадающим частотам, должны быть некоррелированы между собой, а дисперсия неограниченно велика при любых частотах.

Между спектром мощности S_X(w) стационарного случайного процесса X(t) и его корреляционной функцией m_X(t) существует связь, определяемая теоремой Хинчина – Винера, в соответствии с которой спектр мощности S_X(w) стационарного случайного процесса X(t) и его корреляционная функция m_X(t) связаны между собой прямым и обратным преобразованием Фурье

.

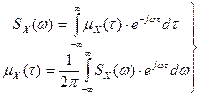Поскольку m_X(t) – четная функция t, а S_X(w) – четная функция w, то эти выражения можно записать, используя интегралы в полубесконечных пределах

.

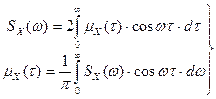Использование этих выражений, а также понятия одностороннего спектра позволяет вычислить дисперсию стационарного случайного процесса путем интегрирования только по положительным, т.е. физическим частотам .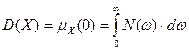

Стационарный случайный процесс со спектром мощности гауссова вида

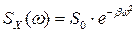
имеет корреляционную функцию

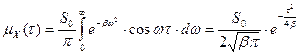
и дисперсию

,

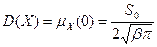откуда можно сделать вывод о том, что гауссов характер спектра мощности приводит к функции корреляции тоже гауссова вида.

По аналогии с интервалом корреляции для временной области вводится понятие эффективной ширины спектра при описании случайных процессов в частотной области.

Пусть случайный процесс X(t) характеризуется односторонним спектром мощности N(w), причем Nmax – экстремальное значение этой функции (рис. 4). Заменим мысленно данный случайный процесс другим, у которого спектральная плотность мощности постоянна и равна Nmax в пределах эффективной полосы частот Dwэф,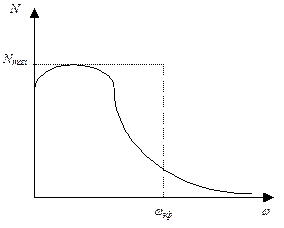
Рис. 4

выбираемой из условий равенства средних мощностей обоих процессов, т. е. 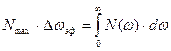, откуда получается выражение для эффективной ширины спектра .

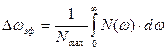Из свойств преобразования Фурье следует, что величины интервала корреляции t_к и эффективной ширины спектра Dw_эф связаны соотношением 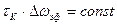, т.е. увеличение интервала корреляции приводит к сокращению ширины спектра и наоборот. Это является общим свойством любой пары функций, связанных преобразованием Фурье.

Стационарный случайный процесс X(t) с равномерной спектральной плотностью 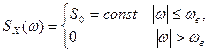в некоторой полосе частот (рис. 5) называют квазибелым шумом по аналогии с белым светом, т. е. электромагнитными колебаниями, имеющими равномерный спектр в области видимых частот.

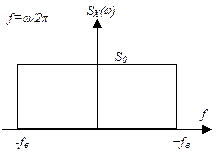
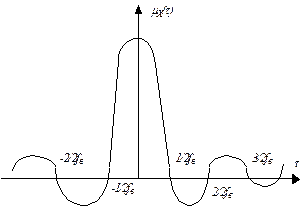
Рис. 5	Рис. 6

Корреляционная функция этого процесса (рис. 6)

.

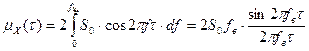Отсюда следует, что при значениях t, кратных 1/2f_в корреляционная функция m_X(t) = 0. Таким образом, сечения процесса, разделенные интервалом k/2f_в, где k - целое число, некоррелированы между собой.

Здесь уместно сделать важное наблюдение. Интервал корреляции t_к, представляющий собой оценку ширины основного лепестка корреляционной функции, связан с величиной f_в соотношением .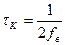

Если беспредельно увеличивать f_в, то придем к процессу, у которого любые два несовпадающих сечения некоррелированы, т. е. функция корреляции равна нулю во всех точках, кроме t = 0 и выражается через дельта–функцию .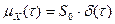

Некоррелированность мгновенных значений такого случайного процесса означает бесконечно большую скорость изменения его во времени - как бы мал ни был интервал t, процесс за это время может измениться на любую величину.

Спектральная плотность такого процесса постоянна на всех частотах, а не в ограниченном диапазоне, а дисперсия бесконечна. Такой процесс называется белым шумом.

Белый шум представляет собой не реальный физический процесс, а абстрактную математическую модель, весьма полезную и широко применяемую. Это обусловлено тем, что на практике часто приходится встречаться с процессами, имеющими равномерную спектральную плотность в полосе частот, которая является гораздо более широкой, чем полосы пропускания цепей, на которые эти процессы воздействуют. В этом смысле белый шум будет адекватной математической моделью.