Глава 3. Случайные процессы

По определению случайный процесс X(t) – это особого вида функция, характеризующаяся тем, что в любой момент времени t принимаемые ею значения являются случайными величинами.

Фиксируя на определенном временном интервале мгновенные значения этой функции, получаем единственную реализацию x₁(t) случайного процесса X(t).

Случайный процесс X(t) представляет собой бесконечную совокупность таких реализаций, образующих статистический ансамбль (рис. 1).

	Фиксируя величины 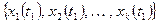, полученные в отдельных реализациях, получаем так называемое одномерное сечениеданного случайного процесса и наблюдаем тем самым случайную величину X(t1).
Рис. 1

Ее плотность вероятности w(x,t₁) называют одномерной плотностью вероятности процесса X(t) в момент времени t₁. Она по определению характеризует вероятность того, что реализации случайного процесса в момент времени t₁ примут значения, лежащие в интервале (x, dx).

Естественным обобщением является n-мерное сечение, приводящее к n-мерной плотности вероятности. Описание случайных процессов с помощью плотностей вероятностей высокой размерности может быть весьма подробным, но приводит к значительным математическим трудностям.

Менее подробное, но вполне удовлетворительное описание случайных процессов можно выполнить с помощью числовых характеристик тех случайных величин, которые наблюдаются в сечениях процессов. Поскольку в общем случае для случайных процессов эти характеристики зависят от времени, они называются моментными функциями.

По аналогии с ранее изложенным математическое ожидание непрерывного случайного процесса есть среднее значение процесса X(t) в текущий момент времени t, причем усреднение проводится по всему ансамблю реализаций процесса .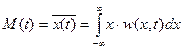

Дисперсия непрерывного случайного процесса, так же определяемая по аналогии, позволяет судить о степени разброса мгновенных значений, принимаемых отдельными реализациями, в фиксированном сечении t относительно среднего значения

.

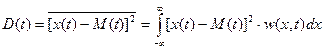Функция корреляции определяется в соответствии с выражением

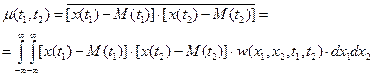
и характеризует степень статистической связи тех случайных величин, которые наблюдаются в сечениях t₁ и t₂. При совмещении сечений t₁ = t₂ = t функция корреляции численно равна дисперсии D(t).

Случайные процессы, статистические характеристики которых одинаковы во всех сечениях, принято называть стационарными.

Говорят, что случайный процесс стационарен в узком смысле, если его любая n-мерная плотность вероятности инвариантна относительно временного сдвига t..

Если ограничиться требованием того, чтобы математическое ожидание и дисперсия процесса не зависели от времени, а функция корреляции зависела лишь от разности 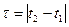, т.е. m(t₂-t₁) = m(t), то такой случайный процесс называют стационарным в широком смысле. Из стационарности в узком смысле следует и стационарность в широком смысле, но не наоборот.

Функция корреляции стационарного процесса является четной, т. е m(t) = m(-t). Кроме того, абсолютное значение этой функции при любых t не превышает ее значения при t = 0, т. е. .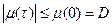

Часто удобнее пользоваться нормированной функцией корреляции 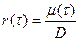, которая при t=0 равна 1, т.е. r(0)=1.

Стационарный случайный процесс X(t) называется эргодическим, если при нахождении его моментных функций усреднение по статистическому ансамблю можно заменить усреднением по времени над единственной реализацией x(t), длительность Т которой может быть сколь угодно велика Т®µ. Это означает, что если стационарный случайный процесс является эргодическим, то его единственная реализация достаточной длины есть «типичный представитель» статистического ансамбля.

Обозначая усреднение по времени угловыми скобками, можно записать для эргодического процесса выражение для математического ожидания 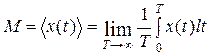, которое имеет физический смысл постоянной составляющей выбранной реализации.

Дисперсия подобного процесса

.

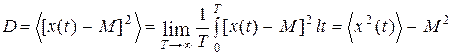Поскольку величина 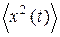имеет физический смысл средней мощности реализации, а величина М² имеет физический смысл мощности постоянной составляющей, то D имеет физический смысл мощности флуктуационной составляющей эргодического процесса.

Аналогично находят функцию корреляции эргодического процесса

.

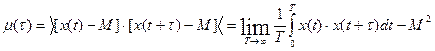Достаточным условием эргодичности стационарного в широком смысле процесса является стремление к нулю функции корреляции при неограниченном росте временного сдвига t, т. е. .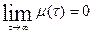

Доказано, что это требование можно несколько ослабить. Оказывается, что стационарный в широком смысле случайный процесс является эргодическим, если выполняется условие Слуцкого .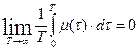

Среди прочих случайных процессов особое место занимает стационарный гауссов процесс – любая его многомерная плотность вероятности определяется двумя характеристиками: математическим ожиданием и функцией корреляции.

Чем быстрее убывает функция m(t), тем меньшей оказывается статистическая связь между мгновенными значениями случайного процесса в два несовпадающих момента времени.

Числовой характеристикой, служащей для оценки скорости изменения реализаций случайного процесса, является интервал корреляции(рис. 2) tк, определяемый выражением .
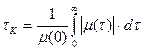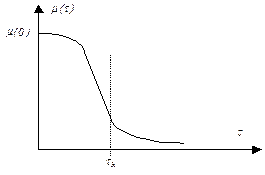
Рис. 2

Смысл этого понятия состоит в следующем. Если известна информация о поведении какой-либо реализации в прошлом, то возможен вероятностный прогноз случайного процесса на время порядка t_к.

Попытка прогнозировать на время существенно большее t_к окажется безрезультатной, поскольку мгновенные значения реализации случайного процесса, сколь угодно далеко отстоящие друг от друга по времени, практически некоррелированы, т.е. среднее значение произведения 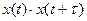стремится к нулю.

Для оценки статистической связи между двумя стационарными случайными процессами X(t) и Y(t) вводится понятие взаимной корреляционной функции (ВКФ) этих процессов, определяемой в соответствии с выражениями

.

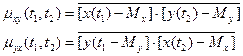Случайные процессы называются стационарно связанными, если их ВКФ зависят не от самих аргументов, а лишь от величины их разности t = t₂ - t₁. В этом случае m_xy(t) = m_yx(-t).

Приведенные ранее выводы о соотношениях независимости и некоррелированности случайных величин справедливы и для случайных процессов.

Обобщая сказанное о случайных процессах, можно сделать следующие выводы:

1. Случайный процесс задается бесконечным ансамблем своих реализаций.

2. Важнейшими характеристиками случайного процесса являются математическое ожидание, дисперсия и функция корреляции.

3. Если статистические характеристики случайного процесса неизменны во времени, то такой процесс называется стационарным.

4. Характеристики стационарного эргодического случайного процесса можно изучать, анализируя единственную его реализацию достаточно большой длины.