Вероятность появления хотя бы одного события

Пусть события 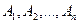независимы всовокупности, причем 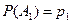, 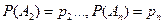;пусть в результате испытания могут наступить все события, либо часть из них, либо ни одно из них.

Вероятность наступления события А, состоящего в появлении хотя бы одного из событий 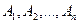, независимых в совокуп­ности, равна разности между единицей и произведением вероятно­стей противоположных событий Ā₁, Ā_{2 , ……,} Ān:

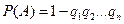
В частности, если все п событий имеют одинаковую вероят­ность, равную p , то вероятность появления хотя бы одного из этих событий

,

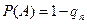42. В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего эле­ментов соответственно равны: р1—0,1;

р2, = 0,15; р3, = 0,2. Найти вероятность того, что тока в цепи не будет.

Решение. Элементы включены последовательно, поэтому тока в цепи не будет (событие A), если откажет хотя бы один из элементов.

Искомая вероятность

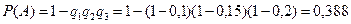
43.Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устрой­ства, если для этого достаточно, чтобы отказал хотя бы один элемент.

44. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7.

45. Три исследователя, независимо один от другого, производят измерения некоторой физической величины.

Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из иссле­дователей допустит ошибку.

46. Вероятность успешного выполнения упражнения для каждого из двух спортсменов равна 0,5. Спортсмены выполняют упражнение по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым полу­чает приз. Найти вероятность получения приза спорт­сменами.

Решение. Для вручения приза достаточно, чтобы хотя бы одна из четырех попыток была успешной. Вероятность успешной попытки р=0,5, а неуспешной q=1—0,5 = 0,5. Искомая вероятность

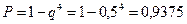
47. Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.

48. Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероят­ность попадания при одном выстреле.

Решение. Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие А) равна

,

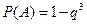где q—вероятность промаха.

По условию, Р(А) = 0,875. Следовательно,

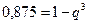, или .

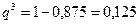Отсюда .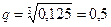

Искомая вероятность

p=1-q=1-0,5=0,5

49. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

50. Многократно измеряют некоторую физическую величину. Вероятность того, что при считывании показа­ний прибора допущена ошибка, равна р. Найти наимень­шее число измерений, которое необходимо произвести, чтобы с вероятностью Р > α можно было ожидать, что хотя бы один результат измерений окажется неверным.

Формула Байеса

Пусть событие А может наступить лишь при условии появле­ния одного из несовместных событий (гипотез) 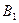, ,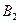… , 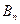кото­рые образуют полную группу событий. Если событие А уже про­изошло, то вероятности гипотез могут быть переоценены по фор­мулам Байеса

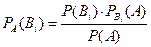(į = 1,2,…..,n),

где

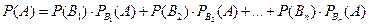
51. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производитель­ность первого автомата вдвое больше производитель­ности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй — 84%. На­удачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь про­изведена первым автоматом.

Решение. Обозначим через А событие — деталь отличного качества. Можно сделать два предположения (гипотезы): B₁—деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй) Р(В₁) = 2/3; В₂ — деталь произведена вторым автоматом, причем Р (В₂)=1/3.

Условная вероятность того, что деталь будет отличного каче­ства, если она произведена первым автоматом, .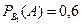

Условная вероятность того, что деталь будет отличного каче­ства, если она произведена вторым автоматом, .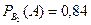

Вероятность того, что наудачу взятая деталь окажется отлич­ного качества, по формуле полной вероятности равна

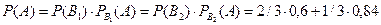
Искомая вероятность того, что взятая отличная деталь произ­ведена первым автоматом, по формуле Байеса равна

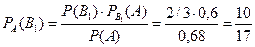
52. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?

53. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероят­ность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.