Энергетический подход к устойчивости упругого стержня

Для исследования устойчивости стержней энергетическим методом получим выражение полной энергии стержня в возмущенном, отклоненном от исходного прямолинейного состоянии.

При решении задач устойчивости, в отличие от задач определения напряженно-деформированного состояния, линейных соотношений, выражающих деформации через перемещения, оказывается недостаточно. В этих соотношениях необходимо удержать и квадратичные члены. В частности, для продольных смещений

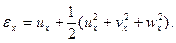(7.1)

Для докритического состояния будем по-прежнему пользоваться линейными соотношениями. В частности,

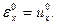(7.2)

Напряженнно-деформированнное состояние стержня будем считать одноосным. Будем считать, что изгиб в закритическом состоянии происходит в плоскости .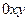

Тогда продольные и поперечные смещения можно представить в виде

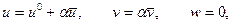(7.3)

где 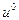- перемещение в докритическом состоянии, a - произвольный малый параметр.

В отклоненном положении на основании (7.1) - (7.3)

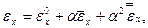(7.4)

где

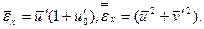(7.5)

Потенциальная энергия тела при одноосном напряженно-деформированном состоянии

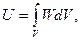(7.6)

где

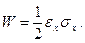(7.7)

Запишем напряжения в форме, аналогичной (7.4):

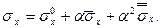(7.8)

Подставим (7.4), (7.8) в (7.7), (7.6) и, ограничившись величинами второго порядка малости, получим для энергии выражение вида

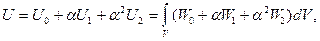(7.9)

где

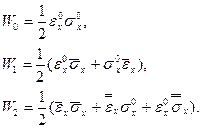(7.10)

Представим работу 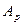внешних сил на перемещениях (7.3) в виде

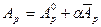, (7.11)

где 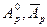- работа внешних сил 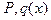на смешениях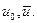

Тогда выражение для полной энергии будет

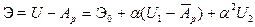. (7.12)

Для исследования вопроса об устойчивости исходного положения равновесия, необходимо располагать выражением для приращения полной энергии при переходе к смежному отклоненному положению

DЭ = Э - Э₀ = 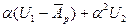. (7.13)

Легко видеть, что первое слагаемое в (7.13)

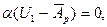(7.14)

поскольку оно представляет собой вариацию полной энергии в исходном равновесном состоянии, которое продолжает оставаться равновесным и при закритических нагрузках, однако это равновесие перестает быть устойчивым.

Таким образом

DЭ = 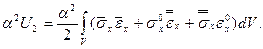(7.15)

Считая, что закон Гука справедлив как в докритическом состоянии, так и в момент потери устойчивости, запишем

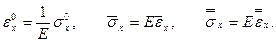(7.16)

С учетом (7.16) выражение (7.15) примет вид

DЭ =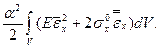

Подставив сюда (7.5), имеем

DЭ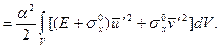

Легко видеть, что величина

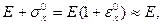
поэтому

DЭ 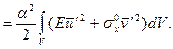(7.17)

Приняв для стержня гипотезу плоских недеформируемых сечений, согласно которой

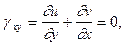
имеем

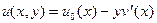, (7.18)

где 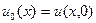- смещение оси стержня.

Сопоставим (7.18) и (7.3)

,

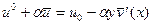откуда заключаем, что

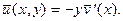(7.19)

Внесем (7.19) в (7.17)

DЭ = ,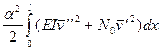

где .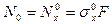

Здесь мы можем отбросить малый параметр 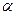, как бы включив его в неизвестную функцию .

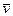Поскольку нагрузка в задачах устойчивости однопараметрическая, представим 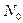в ви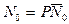де , где 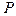- неизвестный параметр критической нагрузки.

Окончательно запишем функционал DЭ в виде

DЭ = 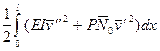. ( 7.20)

Как было показано, к оценке устойчивости существует два разных подхода:

1. точки бифуркации, т.е. соответствующие им значения 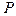, ищутся из условия стационарности функционала (7.20)

d(DЭ) = 0 , (7.21)

2. ищется наименьшее из тех значений 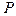, при которых выполняется условие

DЭ = 0 . (7.22)

Распишем условие (7.21), интегрируя в нем выражения для (7.20) по частям. Получим

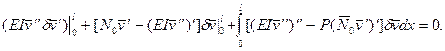(7.23)

Мы получили основное вариационное уравнение устойчивости сжатого прямого стержня.

Из него в силу произвольности и независимости вариаций 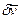внутри интервала и 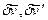- на его концах, вытекают основное линеаризованное уравнение устойчивости (уравнение Эйлера)

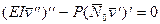(7.24)

и естественные граничные условия

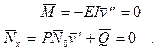либо 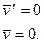(7.25)

Здесь следует обратить внимание на один очень существенный момент. Как уравнение (7.23), так и граничные условия (7.24) записаны относительно возмущенного состояния. Это характерно для задач устойчивости любых объектов. Уравнение (7.24) и условия (7.25) в данном случае совпали с (5.9) - (5.11) только потому, что в исходном положении прогиб отсутствует, то есть 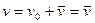. Понимая это, будем в дальнейшем вместо 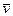писать .

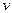Уравнение (7.21) , где функционал DЭ представлен выражением (7.20), называется критерием устойчивости в форме Брайана. Характерная особенность этого критерия состоит в том, что в нем отсутствуют докритические перемещения, но присутствуют докритические усилия .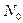

Критерий Брайана позволяет получить решение задачи при любых условиях закрепления концов стержня. Но для того, чтобы им воспользоваться, необходимо предварительно решить задачу о докритическом поведении стержня.

Известна и другая форма энергетического критерия устойчивости, где такую задачу предварительно решать не надо.

Для этого необходимо по сравнению с выражением (7.3) добавить к продольному смещению величину второго порядка малости

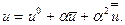
Это повлечет за собой появление некоторых дополнительных членов в записанных выше выражениях.

Так в (7.5)

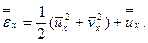(7.26)

В выражении для работы 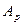внешних сил по сравнению с (7.11) появится член второго порядка малости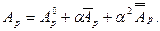

Здесь

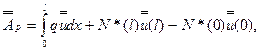(7.27)

где 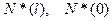- положительные внешние силы (а не реакции опор), если таковые заданы.

Приращение полной энергии 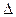Э будет теперь иметь вид

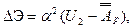(7.28)

где 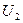по-прежнему определяется выражением (7.15)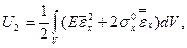

однако, из-за дополнительного члена 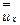в (7.26), оно теперь приведется к виду

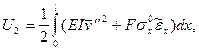(7.29)

где

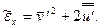(7.30)

Добавочному перемещению 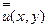можно дать следующую интерпретацию (рис.7.1). Для фиксированного поперечного сечения 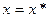: 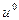- смещение точек сечения стержня за счет докритической деформации; 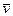- закритический прогиб оси; 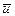- продольные смещения за счет поворота плоского сечения при прогибе оси; 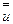- закритическое смещение.

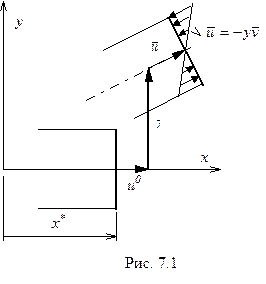
На рисунке все составляющие полного смещения показаны положительными. Если ось стержня считать нерастяжимой, то смещение 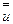будет, естественно, отличным от тождественного нуля.

Чтобы понять суть дальнейших рассуждений, напомним логику использования энергетического критерия. Равновесие перестает быть устойчивым, как только среди возможных перемещений 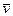появляются такие, которые приводят к 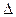Э .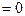

При этом к перемещениям 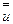предъявляется единственное требование - чтобы они также были возможными, т.е. допускались наложенными на систему геометрическими граничными условиями. Следовательно, не нарушая этих граничных условий, перемещениями 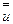можно распорядиться. В частности, положив 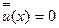, мы получим критерий устойчивости в форме Брайана.

Можно выбрать функцию 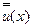и так, чтобы изгнать из (7.28) начальные напряжения 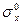(или, что то же самое, - докритические перемещения ).

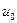С этой целью преобразуем второй член в (7.29)

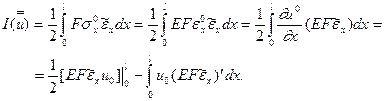(7.31)

Из (7.31) ясно, что для того, чтобы 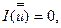необходимо выбрать 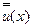так, чтобы выполнялось дифференциальное уравнение

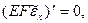(7.32)

связывающее, на основании (7.30), 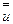с 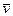зависимостью

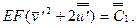(7.33)

Откуда

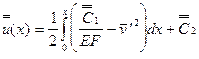. (7.34)

Константы 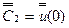и 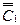определяются из следующих граничных условий: на закрепленном от продольных смещений конце 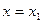дополнительное смещение 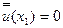; на конце 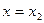, где задана нагрузка, 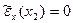, т.е. на основании (7.30) , (7.33) 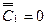. При выбранных таким способом смещениях 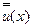энергетический критерий (7.28) имеет вид (множитель a² можно опустить)

DЭ = 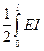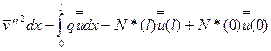. (7.35)

Выражение (7.35) представляет собой энергетический критерий в форме Тимошенко.

Им удобно пользоваться в тех случаях, когда потеря устойчивости стержня может происходить без растяжения его оси, то есть когда один из концов стержня не закреплен от продольных смещений. Тогда 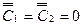, и

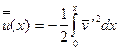. (7.36)

Если при этом распределенная нагрузка отсутствует 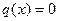и стержень сжат только силой 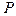на конце, то 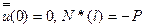и, приравняв DЭ (7.35) нулю, имеем формулу

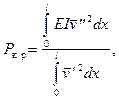(7.37)

удобную для приближенных вычислений.