Линеаризованное уравнение устойчивости сжатого стержня

УСТОЙЧИВОСТЬ ГИБКИХ СТЕРЖНЕЙ

Лекция 5

Задачи устойчивости сжатых стержней, представляющие самостоятельный интерес и практическую ценность, могут служить прекрасной иллюстрацией большинства наиболее типичных, важных и тонких мест, характерных для задач устойчивости более сложных объектов. Некоторые из этих особенностей можно было уловить уже из рассмотренных выше задач устойчивости систем с конечным числом степеней свободы. Однако, упругие сиcтемы, обладающие распределенными параметрами жесткости, могут от них существенно отличаться.

Линеаризованное уравнение устойчивости сжатого стержня

Как уже было показано, задачи устойчивости значительно более чувствительны к детальному характеру нагружения и закрепления систем и к их геометрии, чем задачи определения напряженно-деформированного состояния. Поэтому исследование устойчивости стержней требует дополнительных по отношению к “Сопротивлению материалов” оговорок и ограничений.

Там было приняты допущения:

- о малости перемещений;

- об отсутствии поперечных нормальных напряжений в их сравнении с продольными напряжениями;

- о поперечных сечениях, остающихся плоскими и нормальными к изогнутой оси стержня.

Дополнительно примем следующее:

- ось стержня идеально прямолинейна, нагружение и закрепление осуществля-ется строго по этой оси;

- внешние силы “мертвые”, то есть не меняют ни величины, ни направления;

- в докритическом состоянии стержень напряжен, но недеформирован, то есть он как бы абсолютно жесткий.

В дальнейшем мы рассмотрим и некоторые решения, свободные от принятых допущений. При этом отказ от того или иного будет специально оговорен.

Рассмотрим возможность существования изогнутых положений равновесия сжатого стержня, близких к идеально прямолинейной форме равновесия. Для прямых стержней единственным уравнением равновесия (Рис.5.1а) оказывается

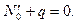(5.1)

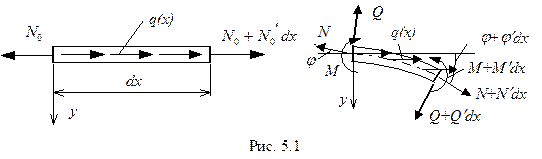
Продольные усилия

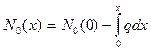(5.2)

будем всегда считать известными.

Запишем линеаризованные уравнения равновесия изогнутого элемента стержня, предполагая угол поворота 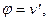где 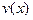- прогиб стержня, и все его производные 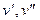- величины первого порядка малости по сравнению с единицей. То есть

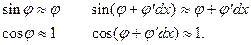
Условие равновесия в проекции на ось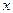

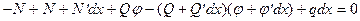
после пренебрежения величиной 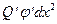принимает вид

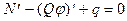. (5.3)

Условие равновесия в проекции на ось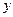

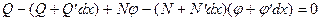
с точностью до бесконечно малых высших порядков

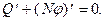(5.4)

Условие равновесия в отношении моментов дает известное соотношение

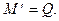(5.5)

В силу гипотезы плоских сечений

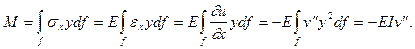(5.6)

Из (5.5)

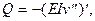(5.7)

и легко видеть, что в уравнении (5.3) величина 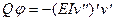пренебрежимо мала вследствие второго порядка малости. В результате уравнение (5.3) совпадает с (5.1) и означает, что в процессе малых искривлений оси стержня предельное усилие 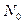не меняется. Таким образом, отклоненное положение равновесия описывается уравнением (5.4) с учетом (5.7):

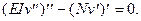(5.8)

Это основное линеаризованное уравнение устойчивости прямых изотропных стержней, имеющее в общем случае переменные коэффициенты и справедливое для любых задач в рамках принятых допущений.

Для случаев, когда вся нагрузка на стержень пропорциональна только одному параметру 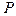, уравнение (5.8) можно переписать в виде

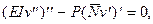(5.9)

где` 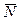- закон распределения продольных усилий в стержне при .

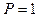Таким образом, задача по поиску нетривиальных форм равновесия представляет собой задачу на собственные значения: найти собственные значения параметра 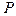, при которых уравнение (5.9) имеет нетривиальные решения (собственные формы), отвечающие однородным граничным условиям. Такая постановка задачи устойчивости стержня называется “эйлеровской”.

Граничные условия задачи устойчивости стержней во многом аналогичны условиям задач поперечного изгиба стержней.

Геометрические условия могут быть только однородными - торец (например 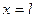) закреплен от смещений 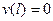или от поворотов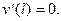

Статические граничные условия для свободного от нагрузки и закрепления торца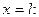

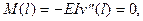(5.10)

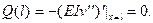(5.11)

Возможны также комбинации однородных геометрических и статических условий, например, свободное (шарнирное) опирание (Рис.5.2а)

(5.12)

или свободное защемление (Рис.5.2б)

(5.13)

Наконец, возможны смешанные граничные условия:

упругого опирания (Рис. 5.2 в)

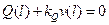(5.14)

или упругого защемления (Рис.5.2г):

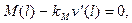(5.15)

также однородные.

Рассмотренные варианты граничных условий не содержали сжимающей силы на торце 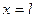, то есть соответствовали сжатию стержней распределенной нагрузкой 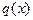или силой на другом торце. При наличии сжимающей силы 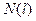к формулировке граничных условий надо подходить особенно внимательно.

Как уже отмечалось, нагрузка предполагается “мертвой” и приложенной строго по оси. Если торец 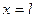при этом заведомо не поворачивается, то

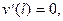
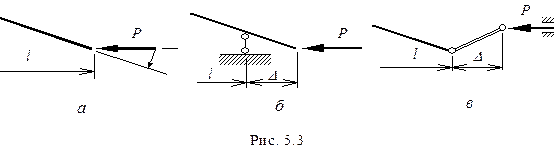
и условие по поперечной силе записываются как обычно. Если же поворот возможен, то продольная сила проектируется на нормаль к оси (Рис.5.3а) и на торце возникает перерезывающая сила

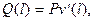(5.16)

то есть условие становится как бы смешанным, но все равно однородным

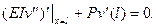(5.17)

Существенное влияние на формулировку граничных условий оказывает также детальный характер приложения сжимающей силы. Для силы, передающейся через жесткий рычаг (Рис.5.3б)

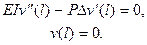(5.18)

Для силы, передающейся через шатун (Рис.5.3в),

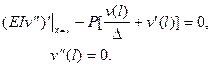(5.19)

В двух последних случаях нагрузка в точке 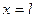оказывается как бы следящей, хотя “мертвый” характер приложения силы 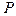сохраняется.

Начнем исследование устойчивости стержней со стержня постоянной жесткости 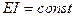при отсутствии распределенной нагрузки 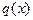, сжатого на конце 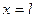силой 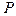. Тогда ` 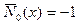, и уравнение (5.9) принимает вид

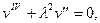(5.20)

где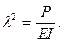

Его общее решение

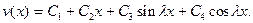(5.21)

При однородных граничных условиях нетривиальное решение (отличное от исходного докритического 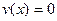) возможно лишь в случае равенства нулю его определителя

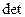A=0 , (5.22)

где A- [4x4] матрица коэффициентов системы уравнений

A C = 0

относительно вектора констант С, выражающего граничные условия.

Уравнения (5.22) всегда трансцендентно и имеет бесконечное множество корней. Это означает, что балка, как и любая система с распределенными параметрами, имеющая бесчисленные степени свободы, всегда имеет бесконечный спектр собственных значений и соответствующих им собственных функций. Наименьшее из собственных значений задачи будет определять критическую силу.