Численное решение основного уравнения. Метод начальных параметров
Основное уравнение устойчивости сжатого стержня (5.9) в общем случае имеет переменные коэффициенты. Это происходит как за счет переменной жесткости стержня 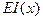 , так и за счет продольной нагрузки
, так и за счет продольной нагрузки 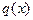 , вызывающей переменное
, вызывающей переменное 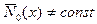 .
.
Решение, а точнее – критическое значение параметра P, приходится искать, например, численно.
Известны разительные численные процедуры поиска 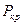 . Рассмотрим одну из них, основанную на сведении краевой задачи для уравнения (5.9) к серии задач Коши. Такой подход принято называть методом начальных параметров.
. Рассмотрим одну из них, основанную на сведении краевой задачи для уравнения (5.9) к серии задач Коши. Такой подход принято называть методом начальных параметров.
При численном интегрировании всегда удобно иметь дело не с одним уравнением высокого порядка, а с эквивалентной ему системой уравнений первого порядка. Для нашего случая такая система фактически уже получена: (5.1), (5.4), (5.5), (5.6).
Перепишем ее в виде
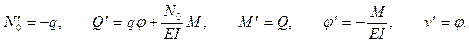 (6.1)
(6.1)
Как отмечалось, усилие 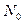 всегда можно считать известным, определив его путем интегрирования первого из уравнений (6.1). Но при численном интегрировании его определение можно включить в общую процедуру.
всегда можно считать известным, определив его путем интегрирования первого из уравнений (6.1). Но при численном интегрировании его определение можно включить в общую процедуру.
Алгоритм удобнее строить в векторной форме, введя вектор 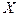
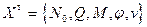 .
.
Задав начальный вектор 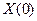 , мы на основании соотношений (6.1) будем знать
, мы на основании соотношений (6.1) будем знать 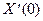 . Затем можно применить одну из процедур численного интегрирования, например, процедуру Рунге-Кутта
. Затем можно применить одну из процедур численного интегрирования, например, процедуру Рунге-Кутта
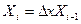 ,
,
где 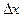 - шаг интегрирования.
- шаг интегрирования.
Отметим несколько существенных моментов.
Поскольку напряженное состояние стержня должно быть однопараметрическим, то есть вызванным единственной причиной, например, силой P, то:
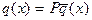 .
.
Из пяти компонент вектора 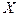 на любом конце стержня всегда известны три: это
на любом конце стержня всегда известны три: это 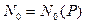 и еще две, определяемые граничными условиями на этом конце.
и еще две, определяемые граничными условиями на этом конце.
Двe неизвестных, оставшиеся константы подлежат определению из граничных условий на другом конце стержня. Их можно определить следующим образом.
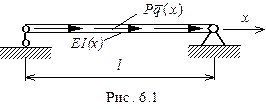
|
Решим путем численного интегрирования две задачи Коши с разными начальными векторами, где на месте двух неизвестных в нуле параметров стоят: в первом случае 1 и 0, а во втором - 0 и 1.
Три остальных параметра известны и в обоих случаях одинаковы.
Поясним это на примере.
Здесь
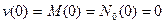 .
.
Начальные векторы решения примем такими
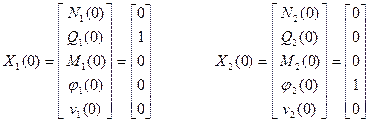
Интегрирование будем производить при некотором выбранном наугад ненулевом значении P. Тогда на конце 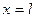 получим некоторые векторы
получим некоторые векторы 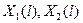 .
.
В силу линейности задачи ясно, что, положив в первой задаче 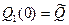 , а во второй
, а во второй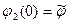 мы получили бы на конце
мы получили бы на конце 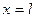
 (6.2)
(6.2)
В этих векторах нас интересуют лишь две компоненты 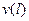 и
и 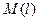 , которые в соответствии с граничными условиями должны быть нулевыми. Из этих условий и будем искать
, которые в соответствии с граничными условиями должны быть нулевыми. Из этих условий и будем искать 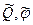 :
:
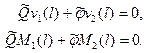 (6.3)
(6.3)
Решение системы (6.3) будет нетривиальным только в случае
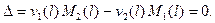 (6.4)
(6.4)
Ясно, что условие (6.4) при произвольно выбранном параметре P не выполнится. Оно выполнится только тогда, когда P - собственные числа задачи.
Итак, задача сводится к тому, чтобы численным перебором P , то есть многократным повторением всей указанной процедуры при разных P, найти наименьшее P, при котором выполнится условие (6.4). Это значение и будет критическим.
Данный алгоритм пригоден при любых переменных коэффициентах. Главное достоинство его - универсальность. Главный же недостаток состоит в том, что при любых изменениях жесткостных, геометрических или нагрузочных факторов задачи, всю численную процедуру необходимо проводить заново. Если для таких простых задач как устойчивость стержней это еще допустимо, то при исследовании устойчивости более сложных пространственных объектов трудоемкость неизмеримо возрастает. Поэтому следует стремиться к тому, чтобы продлить аналитическое решение задачи как можно дальше и в идеале - получить для критических значений параметров если не формулу, то хотя бы трансцендентные уравнения или алгебраические системы.
Ниже мы на примере стержней рассмотрим ряд таких аналитических или полуаналитических подходов.
Рассмотрим способ реализации метода начальных параметров для тех слуаев, когда можно обойтись без процедуры численного интегрирования.
Пусть переменные коэффициенты основного уравнения устойчивости (5.9) кусочно-постоянны. Так будет, если балка имеет ступенчатую жесткость 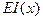 , либо если нагрузка
, либо если нагрузка 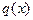 представляет собой систему сосредоточенных сил
представляет собой систему сосредоточенных сил 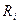 , разумеется, однопараметрическую
, разумеется, однопараметрическую
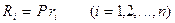 .
.
В этом случае
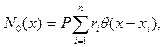 (6.5)
(6.5)
где 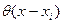 - единичная ступенчатая функция (функция Хевисайда), а
- единичная ступенчатая функция (функция Хевисайда), а 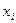 - координата приложения сосредоточенных сил Pri .
- координата приложения сосредоточенных сил Pri .
В рассматриваемом случае на каждом i-том участке уравнение будет иметь вид
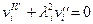 . (6.6)
. (6.6)
Его общее решение
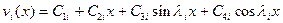 (6.7)
(6.7)
Для балки из 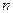 участков решение можно получить, “склеив” в каждой точке стыка решения вида (6.7) между собой, т.е. приравняв в этих точках
участков решение можно получить, “склеив” в каждой точке стыка решения вида (6.7) между собой, т.е. приравняв в этих точках
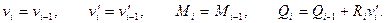 (6.8)
(6.8)
Присоединив сюда граничные условия, получим систему 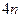 алгебраических уравнений. Критическое значение параметра
алгебраических уравнений. Критическое значение параметра 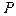 найдется из равенства нулю определителя этой системы.
найдется из равенства нулю определителя этой системы.
Можно поступить и иначе, выразив на каждом участке константы 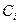 через начальные параметры.
через начальные параметры.
С этой целью воспользуемся выражениями (П-1.1) при 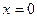 для всех факторов задачи. С их помощью выразим все константы через начальные параметры. Получим
для всех факторов задачи. С их помощью выразим все константы через начальные параметры. Получим
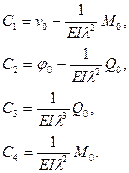 (6.9)
(6.9)
Подставив (6.9) в (6.7) для первого участка, получаем
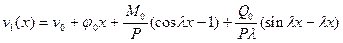 (6.10)
(6.10)
и, соответственно,
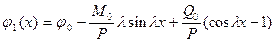 ,
,
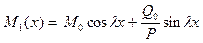 , (6.11)
, (6.11)
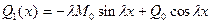 .
.
Таким образом, все факторы внутри интервала и, в частности, на его правом конце выражены через их значения в начале интервала, причем два из этих начальных значений всегда известны или могут быть выражены через два других.
Эта процедура и называется методом начальных параметров.
Переходя к следующему интервалу, пересчитываем значения в конце предыдущего по формулам (6.8). При этом надо помнить, что значения
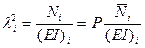
различны, но выражены через один параметр P.
Дойдя таким способом до правого конца и потребовав, чтобы там выполнились два граничных условия, получим однородную систему двух характеристических уравнений. Pавенство нулю определителя этой системы дает спектр собственных значений задачи.
Рассмотренный способ реализации метода начальных параметров отличается от изложенного перед ним только тем, что здесь решение внутри интервала записано аналитически, а там строилось численным интегрированием. Но главное преимущество состоит в том, что здесь параметр нагрузки присутствует в явном виде.
Очевидно, что при достаточно частом делении балки на интервалы этим методом можно исследовать и устойчивость балки с плавно меняющимися коэффициентами путем их кусочно-линейной аппроксимации.
Пример 6.1
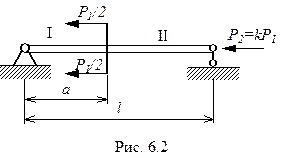
|
На левом конце участка 1:
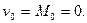 .
.
На правом конце участка 1:
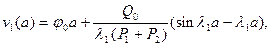
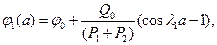 (6.12)
(6.12)
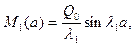
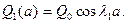
Здесь
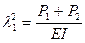 .
.
На правом конце стержня 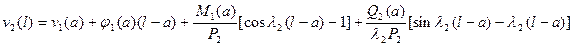
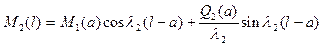 . (6.13)
. (6.13)
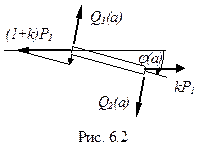
|
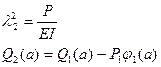
Подставив (6.12) в (6.13), получим систему вида
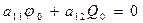
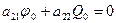
и из условия 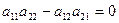 находим
находим 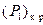 .
.
Пример 6.2
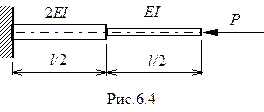
|
Из граничных условий на левом конце
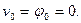
Кроме того, из условия равновесия в проекции на ось y имеем
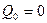 .
.
Из (6.11) имеем
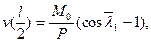

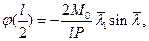
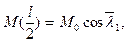
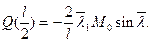 ,
,
где
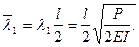
На втором участке
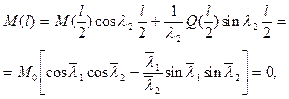
где
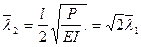 .
.
Поскольку 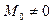 , для отыскания
, для отыскания 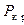 имеем трансцендентное уравнение
имеем трансцендентное уравнение
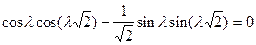 ,
,
где
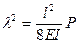 .
.
Наименьшее значение
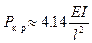 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Линеаризованное уравнение устойчивости сжатого стержня | | | Энергетический подход к устойчивости упругого стержня |
Дата добавления: 2016-09-06; просмотров: 3119;











