ПРЕДМЕТ АЭРОГАЗОДИНАМИКИ

Многие машины и аппараты, созданные к настоящему времени, характеризуются перемещением газа или жидкости внутри их или перемещением самого аппарата в среде газа или жидкости. Проектирование летательных аппаратов и их двигателей невозможно без знания массообменных процессов, протекающих внутри и вне их. Целью курса «Аэрогазодинамика», называемого в дальнейшем также «Механика жидкости и газа» (МЖГ), является изучение явлений, протекающих в газе и жидкости, и закономерностей, которым эти явления подчиняются. Кроме того, необходимо знание таких проблем МЖГ, как динамические и термодинамические процессы в высокоскоростных потоках, ламинарный и турбулентный перенос импульса, движение реальных газов.

Аэрогазодинамика как раздел механики сплошных сред. Реальными материальными частицами, составляющими материальное тело, и, в частности, газ, являются атомы и молекулы. Они находятся в непрерывном хаотическом движении и взаимодействуют между собой за счет сил электромагнитного происхождения. Характер хаотического движения и взаимодействия молекул различен для тел, находящихся в различных агрегатных состояниях. Число материальных частиц (молекул) N в практически малых объемах тела огромно (в 1 см³ твердого тела содержится порядка 10²⁴ молекул). При описании движения каждой молекулы как абсолютно твердого тела для 1 см³ вещества потребовалось бы не менее 6*N ~ 6*10²⁴ дифференциальных уравнений 1-го порядка и такое же число краевых условий. Поэтому изучение движения деформируемых сред чрезвычайно сложно, если рассматривать тело как совокупность реальных материальных частиц. Однако не обязательно знать движение каждой материальной частицы – на практике нужно знать некоторые средние, суммарные характеристики. Это положение определяет два основных подхода к изучению движения деформируемых сред: статистический и феноменологический.

Статистический подход базируется на методах статистической механики. Это - вероятностные методы, применение средних характеристик по большому ансамблю частиц, введение дополнительных гипотез о свойствах молекул и их взаимодействии с целью упрощения модели. Однако при сложном строении молекул использование статистических методов затруднено, так как недостаток информации не позволяет сформулировать гипотезу о взаимодействии молекул, а получаемые уравнения чрезмерно сложны.

Феноменологический подход (от гр. phainomenon - явление) базируется на общих, полученных из опыта, закономерностях и гипотезах, которые принимаются за истинные и используются для построения последующих уравнений и выводов. В основу феноменологического подхода положены понятие материального континуума и соответствующая этому понятию гипотеза сплошности.

Материальный континуум (сплошная среда) есть состоящая из большого числа малых частиц гипотетическая субстанция, которая непрерывно, сплошным образом заполняет область пространства, отведенную данному телу, независимо от его агрегатного состояния. Следует отметить, что под частицей, составляющей материальный континуум, понимается часть тела, малая по отношению к геометрическим размерам тела, но большая по сравнению с размерами молекул. Таким образом, в рамках феноменологического подхода имеет место абстрагирование от реального атомно-молекулярного строения тел и переход к идеализированному представлению вещества в виде материального континуума. Такая идеализация реального дискретного вещества позволяет использовать при исследовании движения деформируемых тел аппарат дифференциального и интегрального исчисления непрерывных функций.

В соответствии с феноменологическим подходом к изучению процессов движения деформируемых сред вводится ряд понятий, качественно определяющих эти процессы, система физических величин, характеризующих их количественно, и между ними на основании опыта устанавливаются взаимосвязи.

Во-первых, вводится система характеристических функций, определяющих движение частиц среды (вектор перемещения d, вектор скорости v, тензоры деформаций (e) и скоростей деформаций, поворота (w) и скоростей поворота) и система параметров, определяющих внутреннее состояние среды (плотность r, удельная внутренняя энергия Е, энтропия S, абсолютная температура Т, давление р, тензор напряжений (s)).

Во-вторых, между введенными физическими величинами устанавливаются взаимосвязи, выражаемые определенными уравнениями и соотношениями, которые основаны на полученных из опыта данных и используются для математического описания поведения сплошных сред. К их числу относятся уравнения, выражающие такие фундаментальные законы природы, как закон сохранения массы (уравнение неразрывности), закон сохранения количества движения (уравнения движения), закон сохранения энергии или первое начало термодинамики (уравнение энергии) и второе начало термодинамики, а также конечные соотношения, отражающие физико-механические свойства изучаемых сплошных сред.

В-третьих, устанавливаются начальные и граничные условия, при которых все характеристические функции могут быть найдены математическими методами.

В данном курсе лекций аэрогазодинамика рассматривается на основе механики сплошной среды (МСС), и, следовательно, в рамках феноменологического подхода при ограничениях и упрощениях, определяемых гипотезами механики сплошных сред.

Первая гипотеза МСС - гипотеза сплошности - связана с понятием материального континуума.

Вторая гипотеза МСС связана с понятием пространства. Под пространством понимается бесконечно большая совокупность точек, однозначно задаваемых с помощью чисел, называемых координатами, которые определяют положение точки относительно начала координат.

Мерность пространства обусловлена числом координат, которыми определяется положение точек в пространстве. Например, бесконечно большая совокупность точек в обычном физическом пространстве составляет трехмерное пространство, так как положение произвольной точки в декартовой прямоугольной системе координат задается тремя координатами: x, y, z. Совокупность точек на плоскости составляет двумерное пространство, положение произвольной точки задается двумя координатами x, y.

Предполагается, что пространство, в котором рассматривается движение деформируемых сред, является евклидовым. Евклидовы пространства – это такие пространства, в которых можно ввести единую для всех точек декартову систему координат х, у, z, а расстояние между двумя произвольными точками 1 и 2 определить по формуле

.

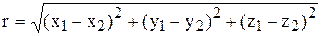Следовательно, обычное физическое трехмерное пространство и двумерное пространство на плоскости являются евклидовыми. Это не относится к двумерному пространству на поверхности сферы, так как нельзя определить расстояние между двумя произвольными точками по приведенной выше формуле, не выходя за пределы этого пространства.

Третья гипотеза МСС – гипотеза абсолютного времени. Согласно этой гипотезе время течет одинаково вне зависимости от выбора системы отсчета, в которой рассматривается движение деформируемой среды. Данная гипотеза является хорошей идеализацией при решении большинства практических задач, в условиях которых скорости движения тел не достигают таких значений, чтобы возникала необходимость учета релятивистских эффектов.

Механика сплошных сред – раздел теоретической физики, в котором изучается движение деформируемых сред: твердых, жидких и газообразных. В отличие от теоретической механики, изучающей движение материальных точек, дискретных систем материальных точек и абсолютно твердых тел, в МСС изучается движение таких тел, которые заполняют пространство непрерывно, сплошным образом и расстояния между точками которых во время движения изменяются. Целью МСС является установление наиболее общих свойств и законов движения деформируемых сред с учетом физико-механических свойств материалов этих сред. Значение МСС состоит в том, что эта дисциплина является основой для более узких, прикладных дисциплин, изучающих движение газов, жидкостей или твердых тел. К их числу относятся: механика жидкости и газа и, в частности, газовая динамика, аэродинамика, гидродинамика; механика деформируемого твердого тела и, в частности, теории упругости и пластичности, теории прочности и разрушения твердых тел и т.д.

Развитие МСС, служащей научной базой многих прикладных технических наук, и в частности – аэрогазодинамики, связано с широким применением математических методов исследования различных процессов и явлений, происходящих в сплошной среде.

Предмет аэрогазодинамики. Основные понятия. Механика сплошных сред, относящаяся к жидким и газообразным средам, – механика жидкости и газа (МЖГ) или гидрогазодинамика. Этот термин вытесняет термин "гидромеханика" или "гидравлика", включающий в себя в основном механику несжимаемой жидкости или течения газов с небольшими скоростями, когда сжимаемостью можно пренебречь. Итак, МЖГ включает в себя гидромеханику – механику несжимаемой жидкости; аэромеханику или аэродинамику, изучающую силовое взаимодействие воздуха с движущимися в нем телами (теория крыла и винта) и движение тел в воздухе при наличии этих взаимодействий (динамика полета); газовую динамику, изучающую движение газа, т.е. сжимаемой среды, в большом диапазоне скоростей (дозвуковых, трансзвуковых и гиперзвуковых). Кроме того, газ, как правило, ограничен некоторым контуром (сопло, камера двигателя, проточные полости лопаток турбин, конфузоры и диффузоры и т.д.). Механика и термодинамика газа, движущегося с большими скоростями, применительно к авиации и ракетной технике, выкристаллизовывается в дисциплину – аэротермодинамику.

Основные свойства принятой модели жидкой или газообразной среды – ее сплошность, т.е. непрерывность распределения массы и физико-механических характеристик среды, лежит в основе кинематики жидкости или газа.

Другое свойство - легкая подвижность или текучесть, т.е. для большинства жидких и газообразных сред касательные напряжения (внутреннее трение) в среде отличные от нуля только при наличии относительного движения сдвига между слоями среды. При относительном покое внутреннее трение отсутствует. Это основное отличие жидкости и газа от упругой среды, в которой касательные напряжения, обусловленные наличием деформаций сдвига (а не скоростей деформаций!) отличны от нуля и при относительном покое среды.

Преимущественно используют две простейших модели газообразной или жидкой среды: идеальной – без внутреннего трения и вязкой – ньютоновской, когда напряжения трения пропорциональны скорости сдвига.

В отличие от газа расстояния между молекулами жидкости крайне малы, что приводит к возникновению значительных молекулярных сил сцепления, особенно интенсивно проявляющихся на внешних поверхностях, отделяющих данную жидкость от другой или от газов. Под действием этих поверхностных сил жидкость подвергается столь сильному сжатию, что малые изменения давлений не меняют объем жидкости. Следовательно, жидкость - среда несжимаемая (кроме явлений гидравлического удара и им подобных).

В газах молекулярные расстояния велики, а силы взаимодействия между молекулами малы. В связи с этим газы обладают свойством сжимаемости.

Механические движения жидкости и газа сопровождаются общими движениями материи – сложными физическими процессами, которыми нельзя пренебречь, ибо иногда они играют главную роль. Поэтому газовая динамика включает в себя:

- движение газа, сопровождающееся химической реакцией горения топлива, когда повышение температуры настолько значительно, что возможна диссоциация молекул и последующая рекомбинация их при охлаждении;

- движение газа при высоких температурах вблизи поверхности тела, движущегося с большой скоростью;

- движение тела в области сильно разреженного газа, требующее применения в азовой динамике (ГД) методов кинетической теории газов;

- движение ионизированного газа (в астрофизике) или ГД магнитных полей.

Для решения выдвигаемых задач МЖГ применяют точные и приближенные математические приемы интегрирования основных дифференциальных уравнений движения, уравнений переноса тепла, вещества и других уравнений, выражающих законы физических процессов в жидкости и газе (например, уравнения электромагнитного поля). Для получения суммарных характеристик явлений используются общие теоремы механики и термодинамики: теоремы количества и моментов количеств движения, закон сохранения энергии и др.

Строгая математическая постановка задач МЖГ приводит к сложным системам дифференциальных уравнений в частных производных, для решения которых необходимо применение вычислительных машин.

Невозможность непосредственного использования уравнений для изучения хаотических, заключающих в себе характерные черты случайности турбулентных движений жидкости или газа, привела к созданию статистических методов изучения такого рода движений.

В МЖГ так же, как и в механике сплошных сред, наряду с векторными величинами приходится рассматривать еще тензорные, которыми являются такие основные физические понятия, как деформация, скорость деформации, напряженное состояние среды, перенос количества движения или другой какой-то векторной величины. При этом особое значение приобретают понятия векторного и тензорного полей с присущими им операциями векторного и тензорного анализов.