Тема 13. Задачи проверки статистических гипотез
Важной задачей математической статистики является задача проверки статистических гипотез.
Статистической гипотезой называется любое утверждение о виде или свойствах функции распределения случайной величины, наблюдаемой в эксперименте.
Сформулированную гипотезу 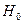 называют основной, совокупность всех распределений, которые не вошли в основную гипотезу, но возможны в рассматриваемой задаче, называют альтернативой и обозначают
называют основной, совокупность всех распределений, которые не вошли в основную гипотезу, но возможны в рассматриваемой задаче, называют альтернативой и обозначают 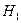 .
.
Задача проверки статистических гипотез заключается в построении правила, позволяющего по конкретному значению выборки 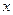 принять или отвергнуть основную гипотезу.
принять или отвергнуть основную гипотезу.
Если в результате проверки гипотезы было принято решение о справедливости альтернативной гипотезы в случае, когда верна основная гипотеза, то говорят, что совершена ошибка первого рода. Вероятность этой ошибки называется уровнем значимости
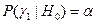 ,
,
где 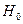 - основная гипотеза,
- основная гипотеза, 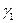 - решение о справедливости альтернативы.
- решение о справедливости альтернативы.
Обычно уровень значимости 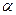 полагают равным 0,1; 0,05; 0,01.
полагают равным 0,1; 0,05; 0,01.
Вероятность принять основную гипотезу при справедливости альтернативы 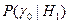 называется ошибкой второго рода.
называется ошибкой второго рода.
Критерием называют случайную величину 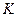 , которая служит для проверки нулевой гипотезы
, которая служит для проверки нулевой гипотезы 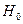 . Множество всех возможных значений критерия разбивают на два непересекающихся подмножества: значения критерия, при которых основная гипотеза отвергается, и значения критерия, при которых нулевая гипотеза принимается.
. Множество всех возможных значений критерия разбивают на два непересекающихся подмножества: значения критерия, при которых основная гипотеза отвергается, и значения критерия, при которых нулевая гипотеза принимается.
Критической областью называют совокупность значений критерия, при которых гипотезу отвергают.
Допустимой областью называют совокупность значений критерия, при которых гипотеза принимается.
Для того, чтобы определить критическую область, определяют критические точки из условия
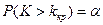 (или
(или 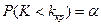 , или
, или 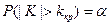 ).
).
Для вычисления значений критерия 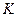 используются специальные таблицы.
используются специальные таблицы.
Дата добавления: 2016-09-06; просмотров: 2188;











