Тема 11. Методы нахождения точечных оценок
- Метод моментов
При заданном виде закона распределения случайной величины  неизвестные параметры этого распределения можно оценить, т.е. выразить как функцию выборки, на основе метода моментов.
неизвестные параметры этого распределения можно оценить, т.е. выразить как функцию выборки, на основе метода моментов.
Этот метод состоит в том, что приравниваются соответствующие теоретические и эмпирические моменты и из полученных уравнений находятся оценки параметров. В случае одного параметра в теоретическом распределении для его оценки достаточно составить одно уравнение. Если имеются два параметра в теоретическом распределении, то нужно приравнять соответственно два теоретических и эмпирических момента и т.д.
Для оценки двух параметров закона распределения запишем следующие равенства:
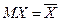 ,
, 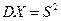 ,
,
где 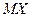 - начальный момент первого порядка закона распределения случайной величины или математическое ожидание;
- начальный момент первого порядка закона распределения случайной величины или математическое ожидание;
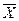 - эмпирический момент первого порядка или выборочное среднее;
- эмпирический момент первого порядка или выборочное среднее;
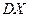 - центральный момент второго порядка закона распределения случайной величины или дисперсия;
- центральный момент второго порядка закона распределения случайной величины или дисперсия;
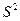 - центральный эмпирический момент второго порядка или выборочная дисперсия.
- центральный эмпирический момент второго порядка или выборочная дисперсия.
Из полученной системы двух уравнений определяем неизвестные значения параметров.
В случае если неизвестен один параметр, то его оценку по методу моментов можно найти из одного уравнения
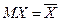 .
.
Пример 1. На предприятии изготавливается определенный вид продукции. Ежемесячный объем выпуска этой продукции является случайной величиной, для характеристики которой принят показательный закон распределения 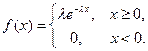
В течение шести месяцев проводился замер объемов выпуска продукции, получены следующие данные:
| Месяц | ||||||
| Объем выпуска |
Найти оценку параметра 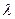 .
.
Решение. Так как закон распределения содержит лишь один параметр 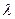 , то для его оценки требуется составить одно уравнение. Находим выборочное среднее:
, то для его оценки требуется составить одно уравнение. Находим выборочное среднее:
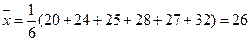
Математическое ожидание случайной величины, распределенной по показательному закону, равно
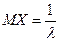 .
.
Получаем следующее уравнение для нахождения неизвестного параметра 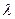 :
:
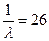 .
.
Откуда находим оценку:
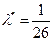 .
.
- Метод максимального правдоподобия
Метод максимального правдоподобия, применяемый для определения точечной оценки, опирается на использование условий экстремума функции одной или нескольких случайных величин. В качестве такой функции принимают функцию правдоподобия.
Для дискретной случайной величины функция правдоподобия принимает вид
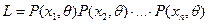 ,
,
где  элементы выборки,
элементы выборки,
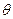 - параметр, для которого находится оценка,
- параметр, для которого находится оценка,
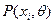 — вероятность события
— вероятность события 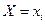 зависящая от параметра
зависящая от параметра 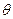 .
.
Для непрерывных случайных величин функция правдоподобия выбирается в виде
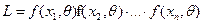
где 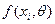 - заданная функция плотности вероятности в точках
- заданная функция плотности вероятности в точках 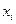 .
.
Так как функции 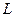 и
и 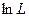 достигают максимума при одном и том же значении
достигают максимума при одном и том же значении 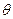 , то обычно точки экстремума находятся для
, то обычно точки экстремума находятся для 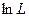 . Для этого определяется производная
. Для этого определяется производная 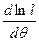 и приравнивается к нулю. На основании достаточного условия (вторая производная должна быть отрицательна) можно убедиться, что полученная точка является точкой максимума.
и приравнивается к нулю. На основании достаточного условия (вторая производная должна быть отрицательна) можно убедиться, что полученная точка является точкой максимума.
Чаще всего метод максимального правдоподобия используется при биномиальном, пуассоновском, нормальном и показательном распределениях случайной величины.
Дата добавления: 2016-09-06; просмотров: 3604;











