Задачи для самостоятельного решения
1.При условии показательного распределения случайной величины  произведена выборка
произведена выборка
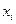
| |||||
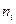
|
Найти оценку параметра 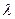 методом моментов и методом максимального правдоподобия.
методом моментов и методом максимального правдоподобия.
2. Случайная величина  распределена по показательному закону с параметром
распределена по показательному закону с параметром 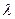 . Произведена выборка
. Произведена выборка
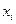
| |||||
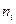
|
Найти оценку параметра 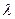 методом моментов и методом максимального правдоподобия.
методом моментов и методом максимального правдоподобия.
3. При условии равномерного распределения случайной величины  на отрезке
на отрезке 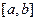 произведена выборка
произведена выборка
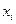
| |||||
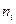
|
Найти оценку параметров 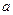 и
и 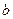 методом моментов.
методом моментов.
4. При условии равномерного распределения случайной величины  произведена выборка
произведена выборка
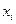
| ||||||||||
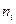
|
Найти оценку параметров 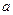 и
и 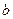 .
.
5. Случайная величина подчиняется нормальному закону распределения. Произведена выборка
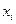
| |||||||
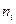
|
Найти оценку параметра а и несмещенную оценку параметра 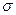 , используя метод моментов.
, используя метод моментов.
6. Случайная величина  распределена по биномиальному закону. Статистическое распределение выборки представлено в таблице:
распределена по биномиальному закону. Статистическое распределение выборки представлено в таблице:
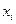
| ||||||||
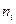
|
Найти точечную оценку параметра 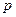 указанного закона распределения случайной величины (
указанного закона распределения случайной величины ( 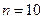 ) методом максимального правдоподобия.
) методом максимального правдоподобия.
7. Случайная величина  распределена по закону Пуассона с неизвестным параметром
распределена по закону Пуассона с неизвестным параметром  . Статистическое распределение выборки представлено в таблице:
. Статистическое распределение выборки представлено в таблице:
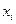
| ||||||||
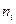
|
Найти точечную оценку параметра 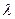 .
.
8. Случайная величина  распределена по показательному закону. Статистическое распределение выборки представлено в таблице:
распределена по показательному закону. Статистическое распределение выборки представлено в таблице:
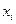
| |||||||
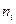
|
Найти точечную оценку параметра 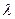 методом максимального правдоподобия.
методом максимального правдоподобия.
9. Стеклянные однородные изделия отправлены для реализации из Москвы в Новосибирск в 1000 контейнерах. После поступления товара было выявлено количество разбитых изделий в каждом контейнере. Результаты представлены в таблице:
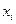
| |||||
|
Считая, что число разбитых изделий описывается законом Пуассона, найти точечную оценку параметра 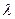 .
.
Дата добавления: 2016-09-06; просмотров: 2674;











