Эмпирическая функция распределения

Важной сводной характеристикой выборки является эмпирическая функция распределения (функция распределения выборки), которая определяется формулой

,

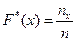где 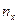– число наблюдений, при которых значение признака меньше 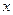, 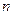– объем выборки.

Свойства эмпирической функции распределения

1. Функция определена на всей числовой прямой.
2. Монотонно не убывает.
3. Является ступенчатой, со скачками в точках .
4. При .
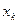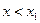
5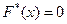. При .

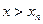
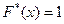Функция 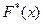при большом числе наблюдений близка в каждой точке к теоретической функции распределения. Поэтому для больших выборок график эмпирической функции распределения дает хорошее приближение к (неизвестной) теоретической функции распределения. В этом смысле о функции 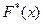говорят как о статистическом аналоге для .

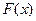Пример 2. Построить по данной выборке эмпирическую функцию распределения и полигон относительных частот

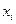
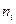
Решение. Объем выборки 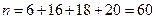. Составим функцию :

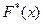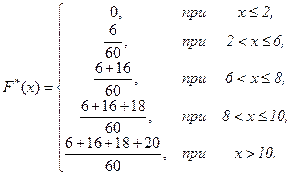
или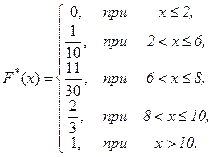

График этой функции изображен на рис. 6.

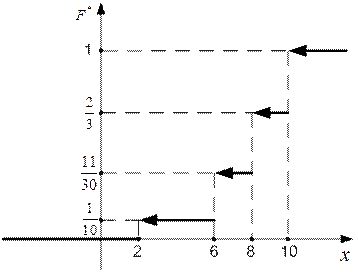
Рис. 6.

По таблице относительных частот построим полигон (рис. 7).

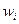
	6/60	16/60	18/60	20/60

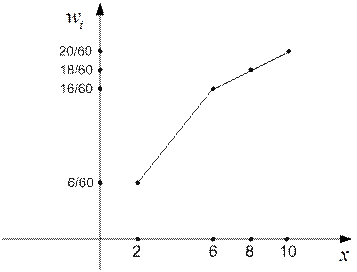
Рис. 7.