Задачи для самостоятельно решения
1. Двумерная случайная величина задана законом распределения:
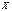
| ||||
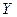
| ||||
| 0,16 | 0,10 | 0,28 | ||
| 0,14 | 0,20 | 0,12 |
Составить законы распределения составляющих. Найти условное математическое ожидание  при
при 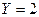 .
.
2. Двумерная случайная величина задана законом распределения:

| ||||
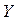
| ||||
| 0,06 | 0,18 | 0,24 | ||
| 0,12 | 0,13 | 0,27 |
Составить законы распределения составляющих. Найти условное математическое ожидание  при
при 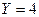 .
.
3. Двумерная случайная величина задана законом распределения:

| ||||
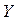
| ||||
| 0,12 | 0,24 | 0,22 | ||
| 0,20 | 0,15 | 0,07 |
Составить законы распределения составляющих. Найти условное математическое ожидание 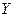 при
при 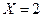 .
.
4. Двумерная случайная величина задана законом распределения:

| ||||
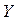
| ||||
| 0,16 | 0,10 | 0,28 | ||
| 0,14 | 0,20 | 0,12 |
Составить законы распределения составляющих. Найти условное математическое ожидание  при
при 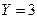 .
.
5. Двумерная случайная величина задана законом распределения:

| ||||
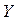
| ||||
| 0,06 | 0,18 | 0,24 | ||
| 0,12 | 0,13 | 0,27 |
Составить законы распределения составляющих. Найти условное математическое ожидание 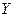 при
при 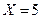 .
.
6. Двумерная случайная величина задана законом распределения:

| ||||
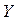
| ||||
| 0,16 | 0,10 | 0,28 | ||
| 0,14 | 0,20 | 0,12 |
Составить законы распределения составляющих. Найти условное математическое ожидание  при
при 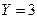 .
.
7. Двумерная случайная величина задана законом распределения:

| ||||
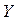
| ||||
| 0,12 | 0,13 | 0,24 | ||
| 0,18 | 0,06 | 0,27 |
Составить законы распределения составляющих. Найти условное математическое ожидание 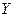 при
при 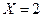 .
.
8. Двумерная случайная величина задана законом распределения:

| ||||
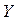
| ||||
| 0,06 | 0,18 | 0,24 | ||
| 0,12 | 0,13 | 0,27 |
Составить законы распределения составляющих. Найти условное математическое ожидание  при
при 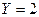 .
.
9. Двумерная случайная величина задана законом распределения:

| ||||
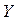
| ||||
| 0,12 | 0,13 | 0,24 | ||
| 0,18 | 0,06 | 0,27 |
Составить законы распределения составляющих. Найти условное математическое ожидание 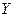 при
при 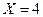 , записать уравнение регрессии
, записать уравнение регрессии 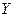 на
на  .
.
10. Двумерная случайная величина задана законом распределения:
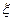
| ||||
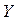
| ||||
| 0,13 | 0,24 | 0,12 | ||
| 0,18 | 0,06 | 0,27 |
Составить законы распределения составляющих. Найти условное математическое ожидание  при
при 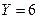 , записать уравнение регрессии
, записать уравнение регрессии  на
на 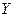 .
.
11. Найти вероятность попадания случайной точки 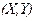 в прямоугольник, ограниченный прямыми
в прямоугольник, ограниченный прямыми 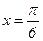 ,
, 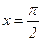 ,
, 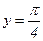 ,
, 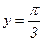 , если известна функция распределения
, если известна функция распределения 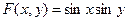 ,
, 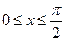 ,
, 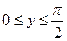 .
.
12. Найти плотность совместного распределения системы случайных величин по известной функции распределения 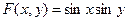 ,
, 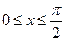 ,
, 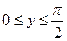 .
.
13. Найти функцию распределения двумерной случайной величины по данной плотности совместного распределения 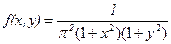 .
.
14. Задана плотность совместного распределения непрерывной двумерной случайной величины 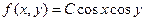 в квадрате
в квадрате 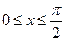 ,
, 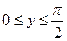 ; вне этого квадрата
; вне этого квадрата 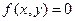 . Найти параметр
. Найти параметр 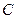 .
.
15. Плотность совместного распределения системы двух непрерывных случайных величин задана формулой
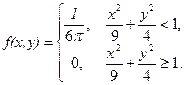
Найти плотности распределения составляющих.
16. Плотность совместного распределения системы двух непрерывных случайных величин задана формулой
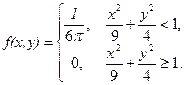
Найти условную плотность вероятности 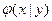 .
.
17. Дана плотность вероятности системы случайных величин 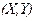 :
:
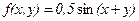 ,
, 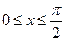 ,
, 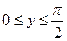 .
.
Определить: а) функцию распределения системы; б) математические ожидания  и
и 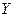 .
.
18. Система случайных величин 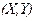 имеет плотность вероятности
имеет плотность вероятности
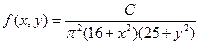 .
.
Требуется: а) определить величину параметра 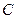 ; б) найти функцию распределения
; б) найти функцию распределения 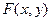 .
.
19. Определить плотность вероятности системы случайных величин 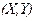 по заданной функции распределения
по заданной функции распределения
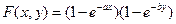 ,
, 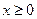 ,
, 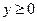 .
.
20. Из отобранных 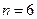 изделий
изделий  оказались кондиционными, среди которых
оказались кондиционными, среди которых 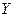 (
(  Ошибка! Ошибка связи.) – высшего сорта. Система
Ошибка! Ошибка связи.) – высшего сорта. Система 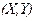 задана следующей двумерной таблицей распределения вероятностей:
задана следующей двумерной таблицей распределения вероятностей:
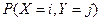
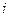
| ||||||||
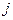
| ||||||||
| 0,202 | 0,174 | 0,113 | 0,062 | 0,049 | 0,023 | 0,004 | ||
| 0,099 | 0,064 | 0,040 | 0,031 | 0,020 | 0,006 | |||
| 0,031 | 0,025 | 0,018 | 0,013 | 0,008 | ||||
| 0,001 | 0,002 | 0,004 | 0,011 |
Требуется: а) составить функцию распределения; б) определить вероятность получения не менее двух изделий высшего сорта; в) определить 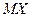 и
и  .
.
21. Плотность вероятности системы случайных величин равна
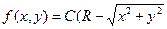 при
при 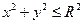 .
.
Определить постоянную 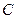 .
.
22. Определить вероятность попадания точки с координатами 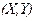 в область, определяемую неравенствами
в область, определяемую неравенствами 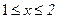 ,
, 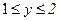 , если функция распределения (
, если функция распределения ( 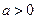 )
)
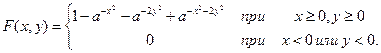
Дата добавления: 2016-09-06; просмотров: 2132;











