Задачи для самостоятельного решения.

1. В течение часа 0 £ t £ 1 (t – время в часах) на остановку прибывает один и только один автобус. Какова вероятность того, что пассажиру, пришедшему на эту остановку в момент времени t = 0, придется ожидать автобус не более 10 минут?

2. Срок службы телевизора распределен по показательному закону со средним сроком службы 5 лет (значит математическое ожиданием l=1/5). Какая вероятность, что телевизор а) прослужит менее 4 лет; б) прослужит более 7 лет; в) поломается на 5 году работы?

3. Случайная величина распределена нормально с параметрами а = 8, s = 3.Найти вероятность того, что случайная величина в результате опыта примет значение, заключенной в интервале (12,5; 14).

4. Число проданного за неделю товара определенного вида Х можно считать распределенной нормально. Математическое ожидание числа продаж 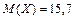тыс. шт. Среднее квадратическое отклонение этой случайной величины s = 0,8 тыс. шт. Найти вероятность того, что за неделю будет продано от 15 до 17 тыс. шт. товара.

5. Производится три независимых выстрела по мосту длиной 20м. Направление стрельбы - вдоль моста. Прицеливание производится по краю моста. Среднее квадратичное отклонение s=60м, математическое ожидание m=0. Для разрушения моста достаточно одного попадания. Найти вероятность того, что мост будет разрушен, если рассеяние при стрельбе подчинено нормальному закону.

6. Все значения равномерно распределенной случайной величины лежат на отрезке [2;8]. Найти вероятность попадания случайной величины в промежуток (3;5).

7. Поезда данного маршрута городского трамвая идут с интервалом в 5 минут. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее чем через минуту после ухода предыдущего поезда, но не позднее чем за две минуты до отхода следующего поезда?

8. Автоматическая телефонная станция получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит точно два вызова?

9. Книга в 1000 страниц имеет 100 опечаток. Какова вероятность того, что на случайно выбранной странице не менее четырех опечаток?

10. Среди семян ржи имеется 0,4% семян сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?

11. вероятность попадания стрелком в мишень равна 2/3. Стрелком сделано 15 выстрелов. Случайная величина - число попаданий в мишень. Найти математическое ожидание и дисперсию случайной величины .

12. Непрерывная случайная величина распределена по показательному закону 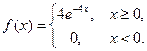. Найти вероятность того, что в результате испытаний попадет в интервал (0,2;0,5).

13. Время 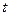расформирования состава через горку – случайная величина, подчиненная показательному закону. Пусть 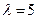- среднее число поездов, которые горка может расформировать за 1 час. Определить вероятность того, что время расформирования состава: 1) меньше 30 минут; 2) больше 6 минут; 3) больше 6 минут, но меньше 24 минут.

14. Вероятность безотказной работы элемента распределена по показательному закону с параметром 0,02. Найти вероятность того, что элемент проработает безотказно в течение 50 часов.

15. Случайная величина распределена по нормальному закону с математическим ожиданием 40 и дисперсией 200. Вычислить вероятность попадания случайной величины в интервал (30;80).

16. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Если стандартная длина равна 40 см и среднее квадратическое отклонение равно 0,4 см, то какую точность длины можно гарантировать с вероятностью 0,8?

17. Масса вагона – случайная величина, распределенная по нормальному закону с математическим ожиданием 65 т и средне квадратическим отклонением 0,9 т. Найти вероятность того, что очередной вагон имеет массу не более 70 т, но не менее 60 т.

18. Мастерская изготавливает стержни, длина которых представляет собой случайную величину, распределенную по нормальному закону с математическим ожиданием и средне квадратическим отклонением, равными соответственно 25 и 0,1 см. Найти вероятность того, что отклонение длины стержня в ту или другую сторону от математического ожидания не превзойдет 0,25 см.

19. Случайная величина подчинена нормальному закону с математическим ожиданием 2,2 и средне квадратическим отклонением 0,5. Какова вероятность того, что при первом испытании случайная величина окажется на отрезке [3;4], а при втором испытании – на отрезке [1;2].

20. Случайная величина распределена равномерно на отрезке [0;4]. Найти функцию распределения, математическое ожидание и средне квадратическое отклонение величины .

21. Паром для перевозки автомашин через залив подходит к причалу через каждые два часа. Считая, что время прибытия автомашин распределено равномерно, определить среднее время ожидания автомашиной прихода парома и дисперсию времени ожидания.

22. Случайная величина распределена по нормальному закону. Математическое ожидание равно 20, среднеквадратическое отклонение равно 3. Найти симметричный относительно математического ожидания интервал, в который с вероятностью 0,9972 попадет случайная величина.

23. Случайная величина имеет показательное распределение с параметром 0,2. Найти вероятность попадания случайной величины в интервал (4;10).

24. Случайная величина распределена равномерно на отрезке [5;7]. Записать выражение для плотности распределения. Найти математическое ожидание и дисперсию.

25. Случайная величина распределена равномерно на интервале [-5;5]. Записать выражение для плотности вероятности. Определить вероятность попадания в интервал (-3;3).

26. Случайная величина распределена по нормальному закону с математическим ожиданием 2, а среднеквадратическим отклонением 3. Найти вероятность попадания в интервал (10;12).

27. Случайная величина распределена по показательному закону с параметром 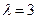. Найти вероятность попадания в интервал (2;4).

28. Записать закон распределения равномерно распределенной на (5;8) случайной величины.

29. Математическое ожидание нормально распределенной случайной величины равно 4, а дисперсия 16. Найти вероятность попадания случайной величины в интервал (12,14).

30. Записать плотность вероятности случайной величины, равномерно распределенной на отрезке [-2;3]. Вычислить математическое ожидание и дисперсию.

31. Случайная величина распределена по нормальному закону с математическим ожиданием 5 и дисперсией 4. Найти вероятность попадания в интервал (3;6).

32. Случайная величина распределена по показательному закону с параметром 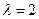. Найти вероятность попадания случайной величины в интервал (1;6).

33. Случайная величина распределена по нормальному закону с параметрами -3, 6. Записать функцию плотности вероятностей и найти вероятность попадания в интервал (3;5).

34. Случайная величина распределена равномерно на интервале (5;10). Найти вероятность попадания случайной величины в интервал (6;8).

35. Случайная величина распределена по экспоненциальному закону с математическим ожиданием равным 2. Записать функцию распределения и плотность

36. Случайная величина распределена равномерно с математическим ожиданием 2 и дисперсией 1/3. Записать закон распределения.

37. Случайная величина распределена по показательному закону с параметром 0,5. Записать закон распределения и найти вероятность попадания в интервал (3;5).

38. Случайная величина распределена по нормальному закону с параметрами 0 и 4. Записать функцию плотности вероятности и найти вероятность попадания в интервал (3;10).

39. Случайная величина распределена по равномерному закону на отрезке [-5;5]. Записать вид функции распределения и плотности вероятности. Найти математическое ожидание и среднеквадратическое отклонение.

40. Случайная величина распределена по нормальному закону в параметрами 2 и 1. Найти вероятность попадания в интервал (-4;2).