Тема 6. Случайные величины
Случайной величиной называется величина 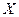 , которая в опыте может принимать одно из множества возможных значений, и до опыта невозможно указать, какое из значений она примет.
, которая в опыте может принимать одно из множества возможных значений, и до опыта невозможно указать, какое из значений она примет.
Например, число мальчиков среди 100 новорожденных – это случайная величина, которая может принимать целые значения от 0 до 100.
Каждое значение случайной величины характеризуется степенью возможности его появления или вероятностью. Если каждому значению случайной величины поставлена в соответствие вероятность принять это значение, то говорят, что задан закон распределения случайной величины.
Про случайную величину говорят, что она «распределена» по данному закону или «подчинена» этому закону распределения.
Случайная величина считается заданной, если задана область ее возможных значений и закон распределения.
В зависимости от области возможных значений случайные величины можно подразделить на дискретные и непрерывные.
Дискретной называется случайная величина, область возможных значений которой есть конечное или счетное множество.
Примеры: число попаданий при десяти выстрелах по цели, выпавшая цифра при подбрасывании игральной кости, количество бракованных изделий в данной партии.
Непрерывной случайной величиной называется случайная величина, область возможных значений которой есть непрерывное множество (отрезок или интервал).
Примеры: дальность полета снаряда; расход электроэнергии за месяц, ошибка, которую мы допускаем при практическом измерении какой-нибудь величины, время безотказной работы того или иного технического устройства.
Строгое определение случайной величины. Случайной величиной 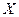 называется числовая функция, определенная на пространстве элементарных событий
называется числовая функция, определенная на пространстве элементарных событий 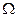 , которая каждому элементарному событию
, которая каждому элементарному событию 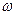 ставит в соответствие число
ставит в соответствие число 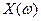 , т.е.
, т.е. 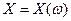 .
.
Дата добавления: 2016-09-06; просмотров: 1883;











