Формы законов распределения непрерывной случайной величины
Непрерывную случайную величину, также как и дискретную, можно задать при помощи функции распределения
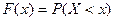 .
.
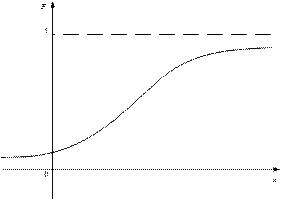
Рис. 4.
Функция распределения непрерывной случайной величины есть непрерывная функция.
Непрерывная случайная величина также может быть задана при помощи функции, называемой плотностью распределения (или плотностью вероятности)
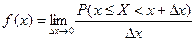
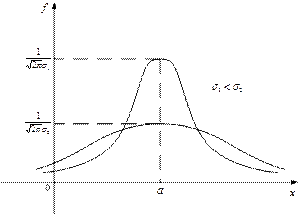
Рис. 5.
Функция распределения и плотность вероятности связаны между собой соотношениями
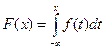 ,
,
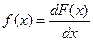 .
.
Свойства плотности вероятности:
1. Плотность вероятности есть неотрицательная функция 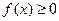 .
.
2. Плотность вероятности удовлетворяет условию нормировки 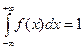 .
.
Свойства функции распределения:
- Функция распределения непрерывна слева.
- Функция распределения – неубывающая функция на всей области определения.
-
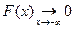 ,
, 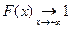 .
. - Для любых
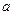 и
и 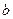 выполнено равенство
выполнено равенство 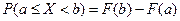 .
. - Функция распределения непрерывной случайной величины есть непрерывная дифференцируемая функция.
- Функция распределения дискретной случайной величины является кусочно-непрерывной и имеет конечное или счетное число скачков.
- Вероятность того, что непрерывная случайная величина примет одно определенноезначение, равна нулю.
Пример 6. Случайная величина 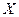 подчинена закону распределения с плотностью
подчинена закону распределения с плотностью
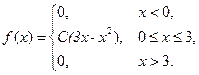 .
.
Требуется найти: 1) параметр С; 2) функцию распределения; 3) вероятность попадания случайной величины в интервал (1;2).
Решение. 1) Для нахождения параметра С используем условие нормировки
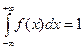 .
.
Поскольку плотность вероятности отлична от нуля только на отрезке [0;3], то интеграл по всему промежутку 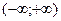 превращается в интеграл
превращается в интеграл
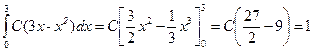 .
.
Отсюда 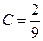 .
.
2) Функция распределения случайной величины вычисляется как интеграл с переменным верхним пределом от плотности вероятности. Поскольку плотность вероятности является кусочно-непрерывной функцией, то интеграл с переменным верхним пределом вычисляется на каждом из промежутков 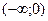 , (0;3),
, (0;3), 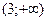 .
.
При 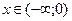 получаем
получаем
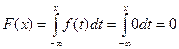 .
.
При 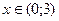 получаем интеграл
получаем интеграл
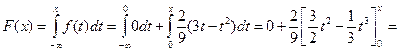
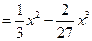 .
.
И, наконец, при 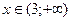 получаем
получаем
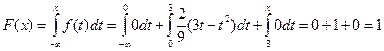 .
.
Таким образом, функция распределения равна
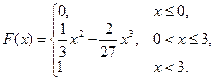
3) Вероятность попадания случайной величины в интервал (1;2) вычисляется по формуле
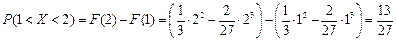 .
.
Дата добавления: 2016-09-06; просмотров: 2541;











