Пересечение поверхностей и тел плоскостями

Многие изделия (детали) являются геометрическими телами пли сочетанием различных геометрических тел. Для построения на чертежах сечений и разрезов изделий надо научиться строить сечения геометрических тел плоскостями (плоские сечения).

В сечении многогранника плоскостью в общем случае полу­чается многоугольник (Рис.15).

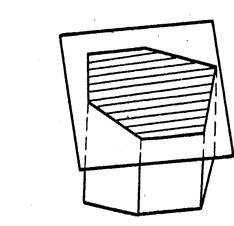
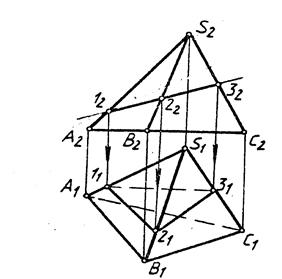
Рис. 15

Линия пересечения поверхности вращения плоскостью стро­ится по точкам. Точки этой линии определяются с помощью вспомогательных секущих плоскостей уровня. В сечении поверх­ности вращения такой плоскостью получается окружность, а секу­щая и вспомогательная плоскости пересекаются по прямой линии. Точки пересечения окружности и этой прямой являются искомыми точками линии пересечения.

Линия пересечения поверхностей вращения плоскостью в ря­де случаев известна заранее и это облегчает ее построение. Обычно построение начинают с опорных и других характерных точек этой линии. К опорным относятся точки: высшая, низшая, левая, правая, ближняя, дальняя.

Пересечение цилиндрической поверхности вращения плоско­стью

(рис. 16) может дать в сечении следующие линии:

а) две прямые (образующие), если секущая плоскость па­раллельна оси вращения;

б) окружность, если секущая плоскость перпендикулярна оси вращения;

в) эллипс, если секущая плоскость не параллельна и не пер­пендикулярна оси вращения.

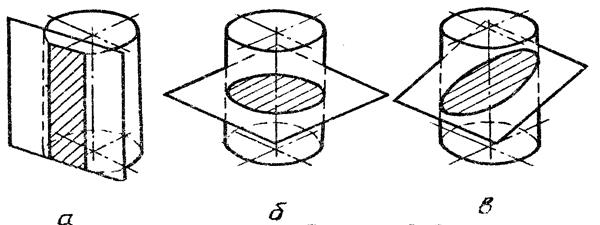
Прямоугольник Окружность Эллипс

Рис.16

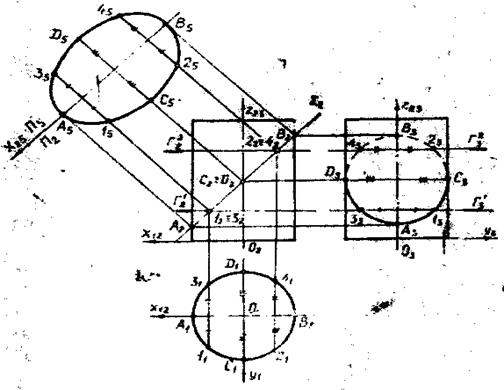
Рис. 17

На рис. 17 показаны проекции наклонного сечения цилиндра вращения фронтально-проецирующей плоскостью ∑ и натураль­ная величина этого сечения — эллипса.

В рассматриваемом примере опорными точками являются концы большой оси эллипса — точки А и В и малой оси эллип­са — точки С и D, проекции которых легко строятся на черте­же. На фронтальной плоскости проекций эллипс изображается отрезком А₂В₂, равным натуральной величине большой оси.

На горизонтальной плоскости проекций все точки эллипса располагаются на горизонтальном очерке цилиндра — окружнос­ти. На профильной плоскости проекций точки эллипса определя­ются по горизонтальным линиям проекционной связи и коорди­нате у, общей для горизонтальной и профильной проекций.

Натуральная величина эллипса может быть определена спо­собом замены плоскостей проекций. Заменим плоскость П₁ на новую плоскость П₅┴П₂ так, чтобы секущая плоскость ∑ заня­ла положение плоскости уровня относительно плоскости П₅. Тогда сечение цилиндра (эллипс) спроецируется на плоскость П₅ в натуральную величину. Для этого новую ось проекций x₂₅ про­водим параллельно фронтальному следу ∑₂ секущей плоскости на произвольном расстоянии от него и линии связи проводим перпендикулярно оси х₂₅. При построении симметричных линий и фигур целесообразно использовать свойства их симметрии. Для эллипса осями симметрии являются его большая и малая оси. Большую ось эллипса А₅В₅ совмещаем с осью х₂₅. Ордина­ты «y» концов малой оси С₅ и D₅ и промежуточных точек эллип­са 1₅, 2₅, 3₅, и 4₅ замеряем на горизонтальной проекции и от­кладываем по линиям связи от большой оси по обе ее стороны. Построенный эллипс с осями А₅В₅ и С₅D₅ является натураль­ной величиной сечения. Штрихами отмечены равные координат­ные отрезки.

В пересечении боковой поверхности конуса вращения плоскос­тями

(рис. 18) получаются следующие линии:

а) окружность, если секущая плоскость перпендикулярна оси
вращения;

б) эллипс, если секущая плоскость не перпендикулярна и не
параллельна оси вращения, но пересекает все образующие;

в) парабола, если секущая плоскость параллельна одной образующей;

г) пересекающиеся прямые, если секущая плоскость проходит
через вершину конической поверхности;

д) гипербола, если секущая плоскость параллельна двум образующим и пересекает обе полы конической поверхности.

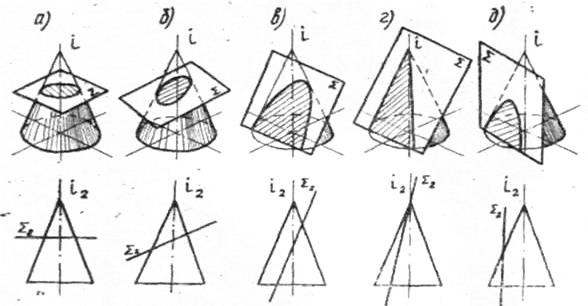
Рис.18

Линия пересечения двух поверхностей в общем случае есть пространственная кривая, точки которой одновременно принадлежат обеим поверхностям.

Общим способом построения точек линий пересечения поверхностей является способ вспомогательных поверхностей-посредников, в роли которых используются или плоскости отдельного положения, или сферы.

Алгоритм построения и его реализация (Рис19) могут быть следующими:

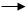1. Заданные поверхности, которые пересекаются, перерезаются вспомогательной плоскостью - посредником частного положения: плоскостью Г║П1 Г┴П2

2. Строят по точкам линии пересечения плоскостью - посредником с каждой заданной поверхностью в отдельности. На рис. 25 пл. Г1 пересекает конус по окружности, а цилиндр по прямым.

3. Находят точки пересечения построенных линий. В нашем примере - двух прямых с окружностью. Эти точки принадлежат обеим пересекающимся поверхностям и являются точками линий их пересечения.

4. Операции 1 ... 3 повторяются несколько раз.

5. На полученных точках строят линию пересечения. Определяют её видимые и невидимые, с данного направления, части линий пересечения.

Рис.19

Вопросы для повторения и закрепления материала

1. Что называется комплексным чертежом и как он образуется?

2. Каким требованиям должны отвечать чертежи?

3. Может ли одна проекция фигуры обеспечить обратимость чертежа?

4. Что принимается за основные плоскости проекций?

5. Как может быть задана линия на комплексном чертеже?

6. Какие прямые являются прямыми общего положения, а какие - частного?

7. Сколько проекций необходимо для задания пря­мой общего положения на комплексном чертеже?

8. В чем состоит особенность изображения прямых уровня на комплексном чертеже?

9. Как называется прямая, одна из проекций которой изображается точкой?

10. Какими способами можно определить величину отрезков прямых общего положения на комплексном чертеже?

Как может быть задана плоскость на комплексном чертеже?

11. Какая плоскость называется плоскостью общего положения и по каким признакам ее можно отли­чить на комплексном чертеже?

12. Какие плоскости называются проецирующими, плос­костями уровня и по каким признакам их можно определить на комплексном чертеже?

13. Как можно определить натуральную величину плос­кой фигуры?

14. Какие разновидности криволинейных поверхностей?

15. Как могут быть заданы криволинейные поверхности на плоскостях проекций?

16. Каким образом могут быть созданы поверхности вращения?

17. Как проверить на комплексном чертеже, принадлежит ли точка поверхности вращения?

18. Как определить точки сечения прямой с телом вращения на комплексном чертеже?

19. Какие кривые можно получить, если плоскость пересекает прямой круговой цилиндр?

20. Какие кривые можно получить, если плоскость пересекает круговой конус?

21. В чем суть общего способа построения линии пересечения поверхностей?