Развертка поверхности

При изготовлении различных технических форм (резервуаров, трубопроводов, сосудов и т.д.) из листового материала изгибанием требуется предварительно построить развертку этих поверхностей. Исходя из этого, большое прикладное значение имеют графические способы построения разверток, которые будут рассмотрены ниже.

Развертка поверхности - фигура, получающаяся после одностороннего совмещения поверхности с плоскостью, при этом каждой точке поверхности соответствует единственная точка на поверхности. Теоретически точно развертываются только гранные поверх­ности, торсы, конические и цилиндрические поверхности (но при этом необходимо помнить, что при построении разверток кониче­ских и цилиндрических поверхностей используется приближенное число π). На рисунке 13а,б представлены развертки параллелепипеда и цилиндра соответственно. Приведенные изображения довольно легко позволяют понять технологию развертки таких поверхностей.

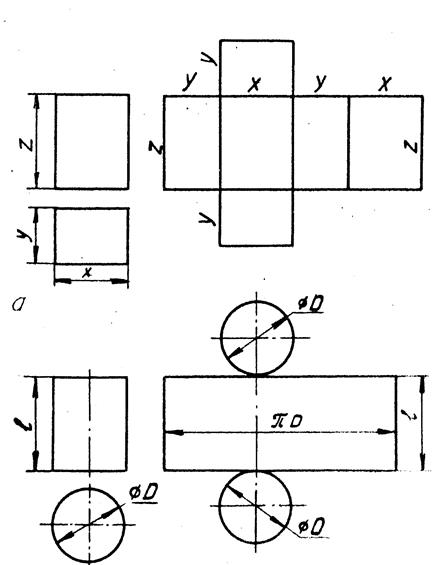
б

Рис. 13

Поверхность прямого кругового конуса (Рис.14) развертывается в сектор с углом при вершине α = (R/l)*360 где R- радиус окружности основания конуса l- длина образующей

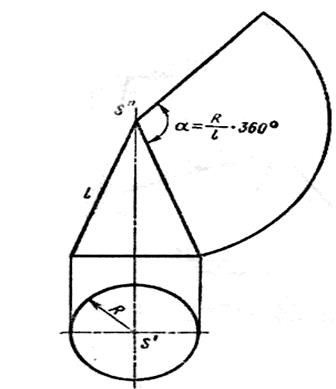
Рис.14 Развертка прямого кругового конуса

Рассматривая развертки развертывающихся поверхностей, необходимо отметить, что на развертке сохраняются:

— длины линий, лежащих на поверхности;

— величины углов между линиями поверхности;

—площади фигур, образованных замкнутыми линиями поверхности, поэтому площадь развертки равна площади развертываемой поверхности.

Для построения разверток неразвертывающихся поверхностей их делят на отсеки (части). Каждый отсек аппроксимируют отсеком соот­ветствующей развертывающейся поверхности. Затем строят развертки этих отсеков, которые в сумме дают условную развертку заданной неразвертывающейся поверхности.