Классификация криволинейных поверхностей и тел. Точки и линии на поверхности

При вращении прямолинейной образующей получаются линей­чатые поверхности вращения (рис.10а, б, в): цилиндрическая, кони­ческая.

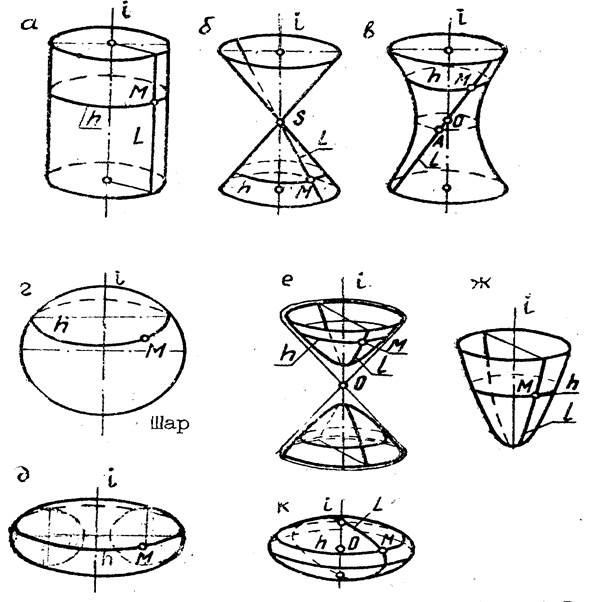
Рис.10 Поверхности вращения

а) цилиндр, б) конус, в) гиперболоид,

г) шар, е) гиперболоид, ж) параболоид,

д) тор, к) эллипсоид

Цилиндрическая поверхность образуется вращением прямой l вокруг параллельной ей оси i, коническая — вращением пря­мой l вокруг пересекающейся с ней в точке S оси i, а поверх­ность однополостного гиперболоида — вращением прямой l вок­руг скрещивающейся с ней оси i. Все эти три по­верхности являются поверхностями вращения второго порядка. Аналитически порядок поверхности определяется степенью ее уравнения, а геометрически — числом точек пересечения поверх­ности с прямой линией.

При вращении криволинейных образующих получаются, как правило, нелинейчатые поверхности. Вращение кривых второго порядка вокруг своих осей симметрии образует поверхности вра­щения второго порядка сферическую, гиперболическую (однопо­лостную и двуполостную), параболическую и др.

Сферическая поверхность (рис. 10г) образуется вращением окружности вокруг оси, проходящей через ее центр, т. е. вокруг диаметра. Если ось вращения не проходит через центр, но ле­жит внутри окружности, образуется поверхность тора закрытого, а если лежит вне окружности — тора открытого (кольца — рис. 10д). Тор — поверхность четвертого порядка.

Поверхность однополостного гиперболоида образуется вращением прямой вокруг скрещивающейся с ней оси (рис. 10в). Вращение гиперболы вокруг действительной оси образует поверхность двуполостного гиперболоида (рис.10е), вращение параболы вокруг ее оси - поверхность параболоида (рис. 10ж).

Следует различать понятия поверхности и тела. Так, напри­мер, цилиндрическая поверхность вдоль образующей бесконечна, а цилиндр — это тело, т. е. часть пространства, ограниченная цилиндрической поверхностью и двумя плоскими основаниями. Аналогично различаются коническая поверхность и конус, сфе­рическая поверхность и шар, и т.д.

При вращении образующей (рис. 11) вокруг оси i все точ­ки образующей, кроме лежащих на оси, опишут на окружности плоскости, которые перпендикулярны оси. Эти окружности называют параллелями, наименьшую из них — горлом, а наиболь­шую — экватором.

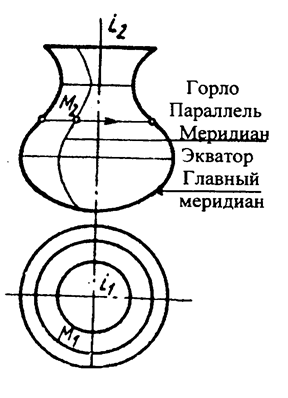
Рис.11 Поверхность, заданная образующей и положением оси

Линия сечения поверхности вращения плоскостью, проходя­щей через ось вращения, называется меридианом. Фронтальный меридиан называют главным. Все меридианы одинаковы, а па­раллели различны.

Каждая параллель пересекает все меридианы под прямым углом. Совокупность параллелей и ме­ридианов образуют на поверхности ортогональную сетку.

На комплексном чертеже ось по­верхности вращения обычно распола­гают перпендикулярно одной из плос­костей проекций. На рис. 11 ось i поверхности вращения перпендикуляр­на плоскости проекций П_1. В этом случае проецируются без искажения:

на плоскость П₁ — все параллели (окружности);

на плоскость П₂ — главный мери­диан, который и определяет фронталь­ный очерк поверхности.

При изучении поверхностей вращения важным является определение условий нахождения точки на поверхности вращения.

Точка принадлежит поверхности, если она принадлежит линии этой по­верхности.

На комплексном чертеже проекции точки должны лежать на одноименных проекциях линии, принадлежащей по­верхности и проходящей через данную точку. В качестве таких линий выби­рают графически простые линии поверхности — прямые или ок­ружности, которые получаются пересечением данной поверхности вспомогательной поверхностью (плоскостью). Алгоритм построения и его реализация (Рис.12) могут быть следующими:

а) выбрать графически простую на данной поверхности линию, проходящую через заданную точку;

б) построить проекции этой линии на чертеже;

в) построить проекции заданной точки на проекциях этой линии.

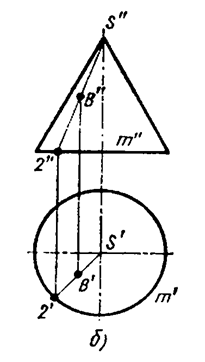
Рис. 12