Правило прямокутного трикутника

Для прямої загального положення виникає потреба у визначенні натуральної величини відрізка та кутів нахилу до площин проекцій. Розглянемо рис. 1.2.11, з якого випливає правило прямокутного трикутника.

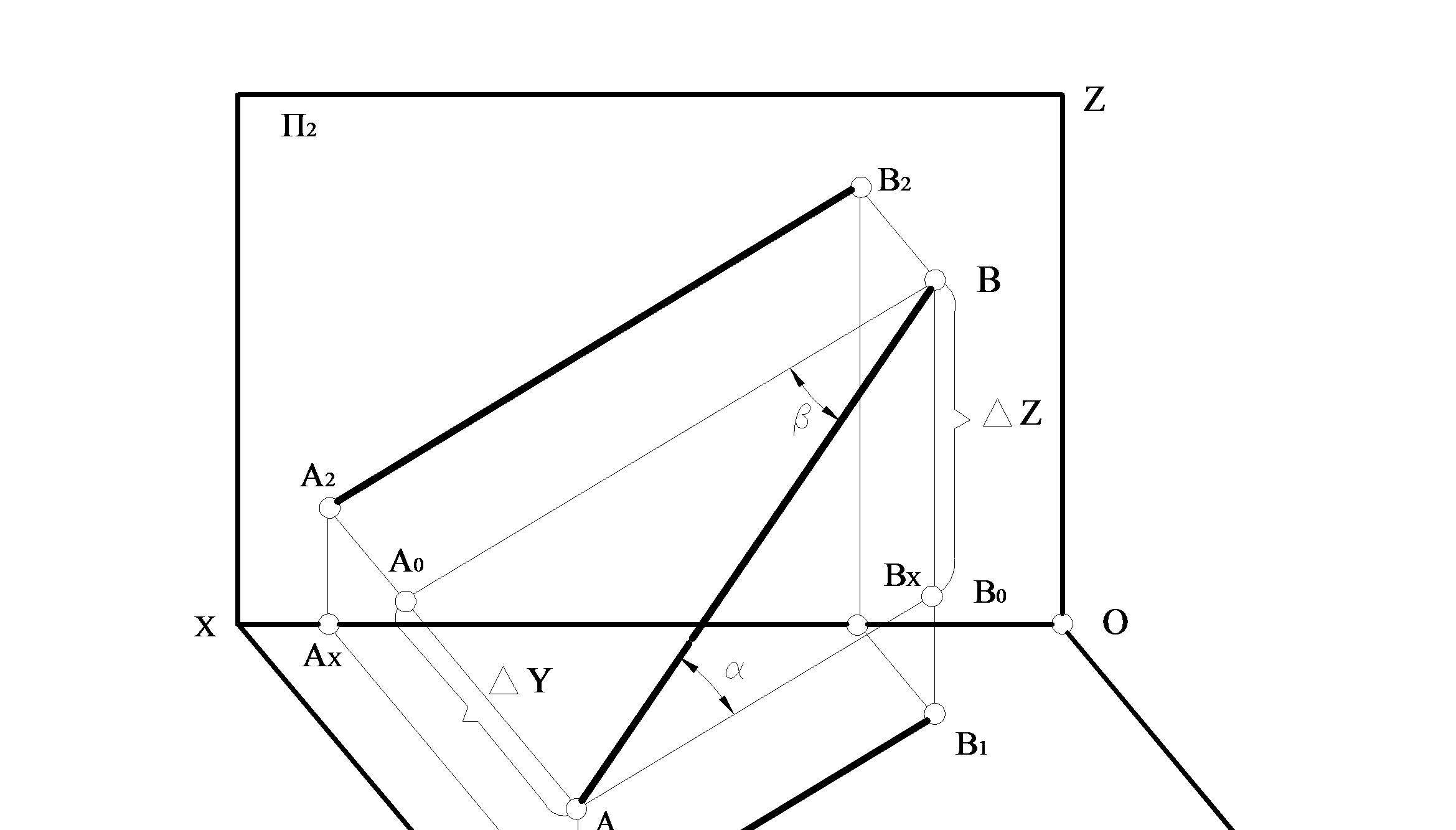
Рисунок 1.2.11

Візьмемо відрізок АВ і побудуємо його ортогональну проекцію на горизонтальну і фронтальну площини проекцій. Розглянемо два прямокутних трикутники ∆АВ₀В і ∆АА₀В, у яких 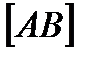– гіпотенуза є натуральною величиною, 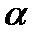= 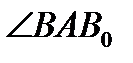– кут нахилу прямої до горизонтальної площини проекцій П₁, 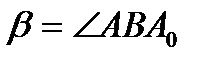– кут нахилу прямої до фронтальної площини проекцій П₂. Для трикутника ∆АВ₀В катет АВ₀ дорівнює величині горизонтальної проекції А₁В₁ відрізка 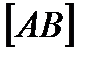, другий катет ВВ₀ дорівнює різниці відстаней від кінців відрізка (точки А і В) до горизонтальної площини проекцій, тобто ∆Z.

Аналогічні висновки випливають також з розгляду трикутника ∆АА₀В.

Для визначення натуральної величини відрізка прямої та кута нахилу прямої до певної площини проекції потрібно на комплексному кресленні (рис. 1.2.12) побудувати прямокутний трикутник на тій площині проекцій, відносно якої визначається кут нахилу прямої, тоді натуральна величина відрізка прямої дорівнює гіпотенузі прямокутного трикутника, одним катетом якого є проекція відрізка на тій площині проекцій, а другим катетом є різниця відстаней від кінців відрізків до тієї ж площини проекцій, а кут між відповідною проекцією цього відрізка та його гіпотенузою дорівнює куту нахилу прямої до цієї площини проекцій.

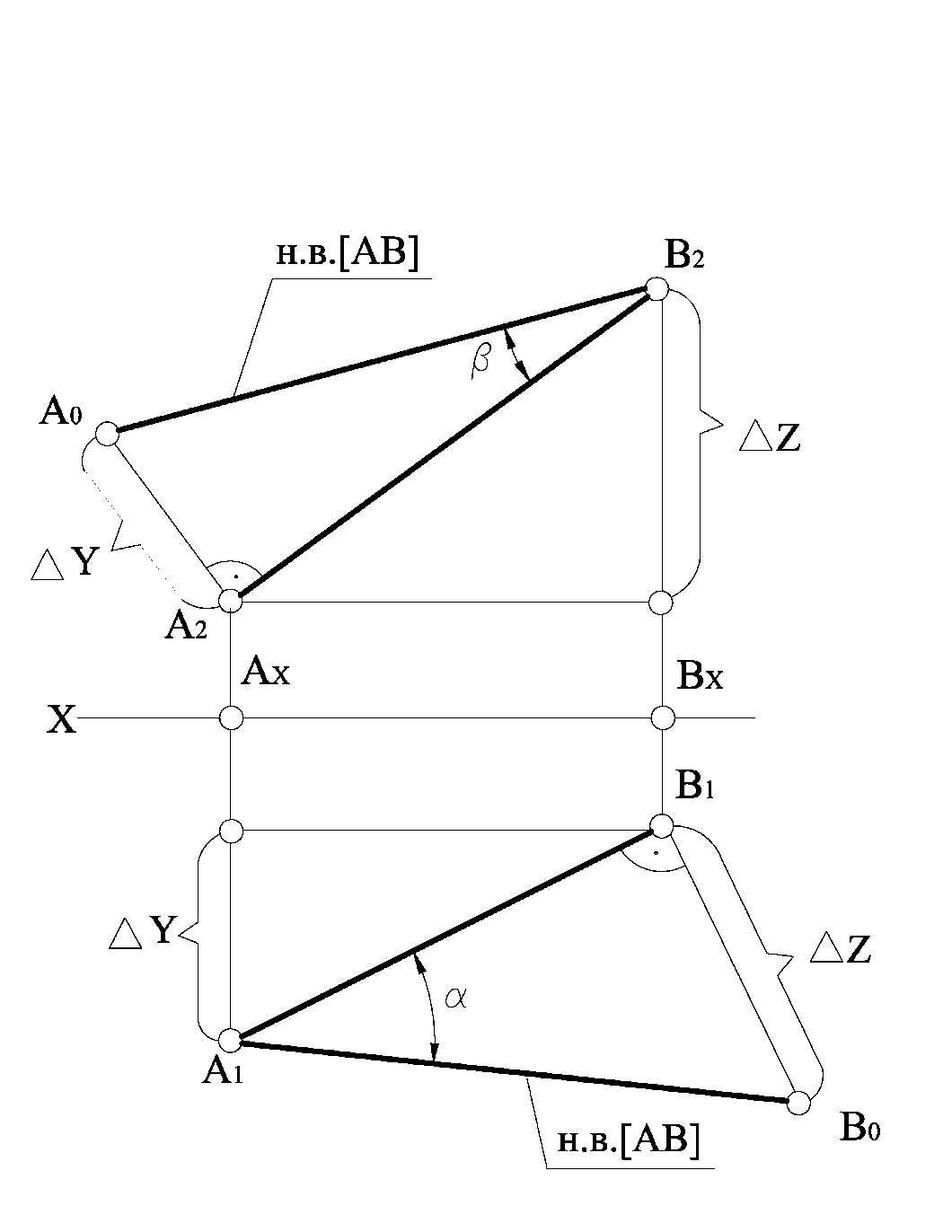
Рисунок 1.2.12