Способ устранения коррелированности регрессоров с остатками с помощью инструментальных переменных

Пусть имеется база данных 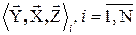. Здесь Z – вектор инструментальных переменных. Пусть выявлена коррелированность 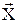с остатками е. Уравнение регрессии дает несостоятельные оценки параметров 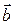. Причем 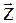– это регрессоры, не коррелированные с остатками (инструментальные переменные).

Идея метода инструментальных переменных: подобрать новые инструменты переменные 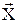, которые бы имели сильную корреляцию с 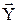и не коррелировали с остатками е.

При этом в качестве { 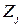} могут выступать те регрессоры из числа { 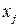}, которые не коррелируют с E, а также другие величины.

Обычно e > m, т.е. число компонент вектора 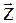больше , чем 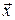. Например, в тесте Уайта при этих переменных коэффициент незначимы.

Далее, исходные регрессоры аппроксимируются через инструментальные независимые переменные и тем самым “очищаются” от коррелированности с E . здесь применяется метод наименьших квадратов (первый шаг). Оценки получаются состоятельными.

Переменные 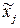, аппроксимированные линейными функциями от инструментальных переменных Z_k называется очищенными (от коррелированности с остатками E) или новыми инструментальными переменными.

В силу линейности всех связей можно связать полученные в итоге состоятельные оценки с Y через исходные регрессоры 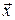. Так мы приходим к алгоритму метода наименьших квадратов.