Двух шаговый метод наименьших квадратов
1. Исходные (неочищенные) регрессоры xj аппроксимируются методом линейных уравнений регрессии от выбранных инструментальных переменных {Zk}, 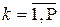 .
.
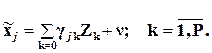 (6.6)
(6.6)
Получаем m ЛУМР, причем, независимых друг от друга (метод наименьших квадратов применяется m - раз). Для этого используется классический метод наименьших квадратов. Здесь { 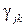 } - матрица искомых коэффициентов; j - номер строки этой матрицы, равный номеру исходного регрессора xj; k – номер члена в ЛУМР, равный номеру инструментальной переменной Zk. Классический метод наименьших квадратов используется поочередно для каждого xj .
} - матрица искомых коэффициентов; j - номер строки этой матрицы, равный номеру исходного регрессора xj; k – номер члена в ЛУМР, равный номеру инструментальной переменной Zk. Классический метод наименьших квадратов используется поочередно для каждого xj .
Замечание. В силу некоррелированности инструмент. переменная Zk с остатками E эти оценки получаются состоятельными метода наименьших квадратов.
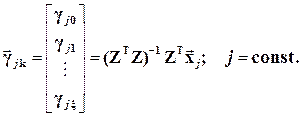 (6.7)
(6.7)
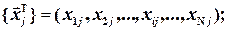 (6.8)
(6.8)
N – число опытов; i – номер опыта;
Z – матрица планирования эксперимента, где базисные функции – линейные функции от Zk.
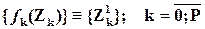
Замечание: переменные 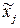 не коррелируют с ошибками регрессии
не коррелируют с ошибками регрессии 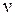 , поскольку они выражаются в виде линейной комбинации некоррелирующих с E переменных {Zk}.
, поскольку они выражаются в виде линейной комбинации некоррелирующих с E переменных {Zk}.
2. Будем рассматривать { 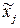 } как новые инструментальные переменные для Y и аппроксимируем Y через них.
} как новые инструментальные переменные для Y и аппроксимируем Y через них.
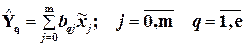 (6.8)
(6.8)
Вектор коэффициентов для каждой фиксированной компоненты 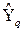 оцениваем снова с помощью классического метода наименьших квадратов:
оцениваем снова с помощью классического метода наименьших квадратов:
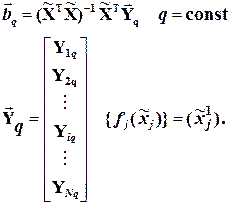 (6.9)
(6.9)
Всего получается таких l формул метода наименьших квадратов вида (6.9); т.е. 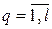 ; где q - число исходных результативных переменных.
; где q - число исходных результативных переменных.
3. Поскольку все преобразования линейны, то подставляя (6.8) в (6.9) получим выражение оценки двухшагового метода наименьших квадратов через исходные (а значит экономически интерпретируемые) инструменты переменной Zj
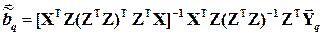 (6.10 )
(6.10 )
Оценки [bjq]состоятельные
Замечание: Для нелинейного МУР применимость 2х – шаговой процедуры сохраняется, однако связь 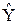 с
с 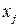 получается уже численная.
получается уже численная.
Вывод:Нужно сделать преобразования переменных перед применением 2х шагов метода наименьших квадратов
Пример: 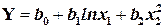
Вводим 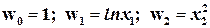
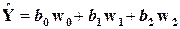 (6.11)
(6.11)
Далее 2х –шаговую процедуру можно применять по стандартной схеме к (6.11)
Второй способ для систем одновременных уравнений (СОУ). Построить НСМ с числом нейронов в выходном слое, равном числу компонентов вектора 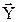
Дата добавления: 2020-12-11; просмотров: 564;











