И ЧАСТОТЫ ВНУТРИМОЛЕКУЛЯРНЫХ КОЛЕБАНИЙ

Силовая постоянная химической связи K(i), равная второй про­изводной полной энергии молекулы по удлинению данной связи q_i, (∂²E/∂q_i ²), является, пожалуй, основной характеристикой механи­ческих свойств связи. Для одноименных связей в разных молекулах сходного типа она варьируется в небольших пределах. Известны полуколичественные корреляции ее с длиной и порядком связи, а также некоторые взаимосвязи с энергией диссоциации.

Химическая связь в многоатомной молекуле, строго говоря, не может быть охарактеризована одним силовым коэффициентом. Для этой цели требуется введение матрицы коэффициентов, вклю­чая те, которые связаны с взаимодействием данной связи и всех других связей, т.е. недиагональные элементы [132,133]: K(i,j) = ∂²E/∂q_i ∂g_j. Последние определяют появление сил, действующих в j-x связях, в результате растяжения i-й связи. Недиагональные элементы, как правило, невелики, но для решения некоторых задач они имеют первостепенное значение.

Если располагать данными о структурной формуле соединения и необходимым набором силовых постоянных, то для изучаемой конформации можно довольно просто вычислить частоты всех нор­мальных колебаний атомов ω, которые проявляются в ИК- и КР-спектрах, электронно-колебательных спектрах поглощения и вто­ричного излучения. Можно также определить формы нормальных колебаний и охарактеризовать силовое поле в как угодно дефор­мированной молекуле. Эти возможности лимитируются недоста­точностью сведений о самих силовых постоянных, которые особен­но ограниченны для электронно-возбужденных состояний.

Общее количество информации, требующейся для точного рас­чета частот ω сложных молекул, весьма велико, и имеющиеся отрывочные данные приходится дополнять, используя аналогии, а иногда и весьма сомнительные допущения. В этих условиях привлечение дополнительных данных представляется очень важ­ным. Квантовая химия занимает здесь особое место, так как позволяет в принципе не только оценить любые силовые постоян­ные как для основного, так и для электронно-возбужденных состоя­ний, но и выяснить для отдельных коэффициентов их происхожде­ние и связь со строением электронной оболочки, чему, к сожале­нию, пока не уделялось достаточного внимания.

Известно, что решение обратной задачи, т.е. вычисление силовых коэффициентов по известным из эксперимента колебательным частотам, требует большой и трудной подготовительной работы по синтезу изотопных моделей. Во многих случаях решение неоднозначно и выбор между наборами коэффициентов, удовлет­воряющих исходной системе уравнений, основывается нередко на интуиции. Привлечение методов квантовой химии дает в распо­ряжение исследователя независимые критерии для такого выбора. К сказанному можно добавить, что квантовохимический расчет силовых постоянных не связан с какими-либо дополнительными трудностями и может быть выполнен обычными методами, описан­ными во введении.

Для расчета силовых постоянных довольно широко применяют как полуэмпирические, так и неэмпирические методы квантовой хи­мии. В любом случае сначала оптимизируют геометрию, т.е. опре­деляют наиболее устойчивую конформацию, отвечающую минимуму полной энергии; затем вычисляют вторые производные полной энер­гии по декартовым или естественным координатам (силовые постоян­ные), а при необходимости - кубичные и биквадратичные члены.

Выбор базиса существенно сказывается на результатах неэмпи­рических расчетов силовых постоянных (в особенности недиаго­нальных элементов). Так, при использовании минимального слейтеровского базиса согласие с экспериментом получается весьма посредственное. Точность расчета существенно повышается при пе­реходе к валентно-расщепленному базису (4-31ГФ, 4-21ГФ или 3-21ГФ), но его дальнейшее расширение уже малоэффективно. При выходе на так называемый хартри-фоковский предел силовые постоянные ока­зываются завышенными на 10 - 20% [134], при этом точность расчета недиагональных элементов намного ниже. Так, для молекулы СО₂ зна­чение К(С—О, С—О^/) получилось завышенным почти в 2 раза [135]. Учет электронной корреляции улучшает результаты [136, 137], однако для многоатомных молекул он практически недоступен.

Для полуэмпирических методов характерно относительное заниже­ние частот деформационных колебаний по сравнению с валентными. При этом в методе ППДП/2 без введения поправок значения колебательных частот для деформационных мод хорошо согласу­ются с экспериментом, а данные для валентных колебаний полу­чаются сильно завышенными. В методе МЧПДП последние, напро­тив, близки к опытным данным, но частоты деформационных колебаний занижены. Методы МЧПДП/3 и МПДП дают результаты промежуточного типа: значения частот для валентных колебаний получаются немного завышенными, а для деформационных - зани­женными. Ошибки при использовании методов МЧПДП/3 и МПДП получаются примерно такие же, как в неэмпирических расчетах без учета электронной корреляции (в среднем около 200 см^-1).

В связи с тем, что ошибки в большинстве случаев носят систе­матический характер, их удается значительно уменьшить введе­нием эмпирически подобранных масштабных корректирующих мно­жителей для определенных типов силовых постоянных (например, для связей С—С, углов С—С—Н и т.д.) или инкрементов, которые прибавляются к рассчитанным частотам.

Для расчетов методами МЧПДП/3 и МПДП Дьюар и Форд [138, 139] подобрали систему инкрементов, специфичных для валент­ных, деформационных и торсионных колебаний определенных атомных групп или связей; на очень большом числе примеров продемонстри­рована удовлетворительная точность результатов. Однако много­образие форм нормальных колебаний, которые в сложной молекуле включают колебания многих связей и углов, и невозможность чет­кого разграничения валентных и деформационных мод ограничивают перспективы корректирования частот по типам колебаний.

Более логичным представляется корректирование значений си­ловых постоянных, и на этом пути достигнуты положительные результаты. В настоящее время используется несколько методик подбора корректирующих множителей. Они различаются способом корректировки недиагональных силовых коэффициентов. В' работе [140] предложено корректировать только диагональные силовые постоянные, а недиагональные оставить без изменений. Этот подход использован в работе [141], в которой методом МЧПДП/3 рас­считаны частоты нормальных колебаний этана, пропана, этилена, бутена-2 и 1,3-бутадиена. Для улучшения количественного согласия с экспериментом были уменьшены силовые постоянные валентных связей на 30%, увеличены силовые постоянные валентных и торсион­ных углов на 20%, а недиагональные коэффициенты оставлены без изменений. Частоты нормальных колебаний исследованных соедине­ний, вычисленные с такой корректировкой силового поля, отлича­ются от экспериментальных значений в среднем на 50см^-1.

Блом и Алтона [142 - 144] использовали один общий коррек­тирующий множитель для всех недиагональных силовых постоянных. Так, при неэмпирическом расчете в базисе 4-31ГФ колебательных спектров этилена ими использовано пять корректирующих множи­телей порядка 0,75 - 1,0. Из них четыре - для диагональных си­ловых постоянных и один - для всех недиагональных членов. При этом среднее расхождение с наблюдаемыми на опыте 12 колеба­тельными частотами уменьшилось более чем в 10 раз и составило около 7 см^-1 [142]. Подобные результаты получены и для этана, пропана, пропена и диметилового эфира, но корректирующие ко­эффициенты подбирались для каждого соединения индивидуально [143, 144]. Отметим, что простое определение частот по набору коэффициентов, полученных из опыта для других молекул сходного типа, дает при отсутствии сопряжения примерно такую же точность.

В работах Пулея с сотрудниками [145, 146] предложено подбирать значе­ния корректирующих множителей только для диагональных членов, а корректирующие множители для недиагональных коэффициентов вычислять как среднее геометрическое из соответствующих диаго­нальных величин, т.е. если С_i и С_j - корректирующие множители для K(i) и K(j), то корректирующий множитель для K(i,j) - 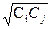. В настоя­щее время методика Пулея используется наиболее широко.

Первые работы с использованием корректирования силового поля молекулы по методике Пулея выполнены полуэмпирическими метода­ми. Так, было показано [146], что при расчете колебательных частот углеводородов методом ППДП/2 следует ввести следующие корректирующие множители: 0,38 для силовых постоянных валентных связей; 0,80 для силовых постоянных валентных углов; 0,62 для силовых постоянных углов выхода из плоскости молекулы. Такие же поправки были использованы для глиоксаля и акролеина [147]. Набор масштабных множителей для органических соединений, содер­жащих атомы N и О, рекомендован и опробован в работе [148], при этом среднеквадратичная ошибка в ряду весьма сложных триазолов не превышала 30 см^-1.

Были рассчитаны [149] частоты нормальных колебаний 4Н-пиран-4-она методами ППДП/2 и МЧПДП/3. Для каждого метода подобран свой набор корректирующих множителей; при этом предполагалось, что их значения для связей и углов, образованных разными ато­мами, различаются. В случае метода ППДП/2 значения вычисленных корректирующих множителей для валентных связей лежат в области 0,25 - 0,45; для валентных углов в плоскости молекулы — 0,83 - 1,20; для углов выхода из плоскости молекулы — 0,65 - 0,80. При использо­вании метода МЧПДП/3 значения подобранных корректирующих множителей для валентных связей лежат в области 0,70 - 0,80; для валентных углов — 1,15 - 1,30; для углов выхода из плоскости мо­лекулы — 1,20 - 1,30. Средние отклонения рассчитанных колебатель­ных частот от экспериментальных величин в случае метода ППДП/2: для плоских колебаний 20 см^-1, для неплоских колебаний 33 см^-1; в случае метода МЧПДП/3: для плоских колебаний 25 см^-1, для неплоских колебаний 17 см^-1.

Опубликовано много неэмпирических расчетов силовых полей и колебательных спектров молекул небольшого и среднего размеров с использованием методики Пулея [145, 150 - 152]. Для малых мо­лекул расхождения между вычисленными и экспериментальными частотами нормальных колебаний составили несколько обратных сантиметров [145, 150]. Для молекул среднего размера это расхож­дение несколько больше. Так, для 1Н-пиррол-2,5-диона среднеквадратичное отклонение вычисленных частот нормальных колебаний от экспериментальных величин составило 7 см^-1 для плоских и 10 см^-1 для неплоских мод [151], для имидазола эти величины равны соответственно 9 и 27 см^-1 [152].

При подборе масштабных множителей или инкрементов естест­венно встает вопрос об их воспроизводимости в ряду разных мо­лекул. В табл. 3.1 приведены корректирующие множители для 1Н-пиррол-2,5-диона.

Близкие значения коэффициентов из наборов 1 и 2 демонстрируют хорошую переносимость корректирующих множителей между молекулами, которые не являются родственными, но содержат од­нотипные валентные связи и углы. Может показаться, что вопрос о переносимости корректирующих множителей сходен с вопросом о переносимости определенных из опыта силовых постоянных, но в действительности происхождение ограничений универсальности в этих двух случаях совершенно различно; в первом случае в основе ограничения лежит существенная иррегулярность ошибок выбранного метода расчета, а во втором - реально существующая специфика силового поля у тех или иных исследуемых молекул, которая сама по себе чрезвычайно интересна и важна для химии и к тому же доступна для изучения квантовохимическими методами.

Таблица 3.1