Системы линейных уравнений с двумя переменными
8.3. Основные понятия
Определение: Линейным уравнением с двумя переменными называется уравнение вида 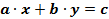 , где x, y – переменные, a, b, c – некоторые числа.
, где x, y – переменные, a, b, c – некоторые числа.
Определение: Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное числовое равенство.
Пример:2x – y = 5 – линейное уравнение с двумя переменными x и y.
(0; –5); (2; –1); (5; 5) – решения линейного уравнения 2x – y = 5.
Вывод:
- Линейное уравнение с двумя переменными
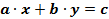 имеет бесконечное множество решений.
имеет бесконечное множество решений.
2.
| -1 |
| -5 |
| х |
| у |
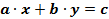 является прямая).
является прямая).
Пример: 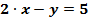 или
или 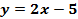
| x | ||
| y | – 5 | – 1 |
Определение: Система линейных уравнений с двумя переменными имеет вид 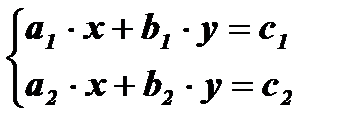
a1, а2 - коэффициенты при x,
b1, b2 - коэффициенты при y,
c1 , c2 - свободные члены.
Определение: Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное числовое равенство.
Определение: Решить систему уравнений – значит найти все ее решения или доказать, что их нет.
8.4. Решение систем линейных уравнений с двумя переменными графически, подстановкой, сложением
| х |
| -3 |
| у |
| -2 |
| l1 |
| l2 |
| М |
1. Графический способ
Пример:Решить графически систему уравнений:
1) 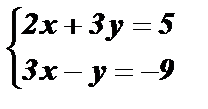
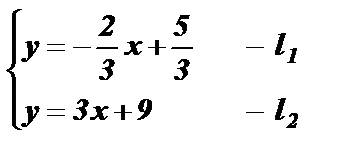
l1: l2:
| x | - 2 | x | - 3 | |||
| y | y |
Координаты любой точки прямой l1 являются решениями уравнения 2x + 3y = 5.
Координаты любой точки прямой l2 являются решениями уравнения 3x – y = – 9.
Координаты x = – 2, y = 3 точки М пересечения прямых l1 и l2 удовлетворяют обоим уравнениям системы, то есть являются решением системы.
Ответ:(- 2; 3) – единственное решение системы.
| y |
| 1 |
| -1 |
| 0 |
| x |
| l1(l2) |
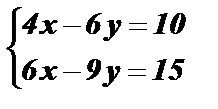
y = 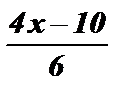 ; y =
; y = 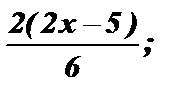 y =
y = 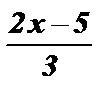 – l1
– l1
y = 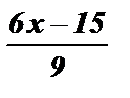 ; y =
; y = 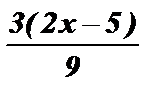 ; y =
; y = 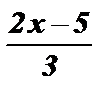 – l2
– l2
Прямые l1 и l2 совпадают. Координаты любой точки прямой являются решениями обоих уравнений системы.
| х | ||
| у | - 1 |
| х |
| y |
| l1 |
| l2 |
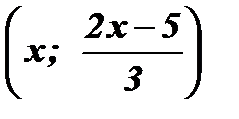 .
.
3) 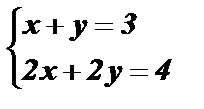 Û
Û 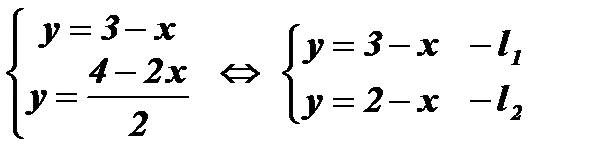
l1: l2:
| х | х | |||||
| у | у |
Прямые l1 и l2 параллельны и не имеют общих точек.
Ответ:Система не имеет решений.
2. Способ подстановки
1) Выразить из какого-нибудь уравнения системы одну переменную через другую.
2) Подставить в другое уравнение системы вместо этой переменной полученное выражение.
3) Решить получившееся уравнение с одной переменной.
4) Найти соответствующее значение другой переменной.
Пример:Решить систему уравнений способом подстановки:
1) 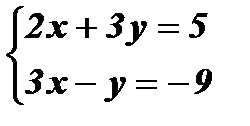 Û
Û 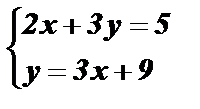 Û
Û 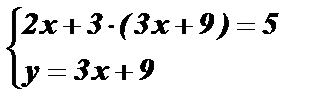
2x + 9x + 27 = 5; 11 x = – 22; x = – 2;
y = 3× ( – 2) + 9; y = 3.
Ответ:( –2; 3)
2) 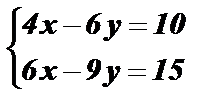 Û
Û 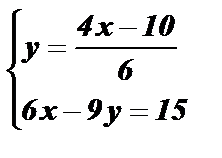 Û
Û 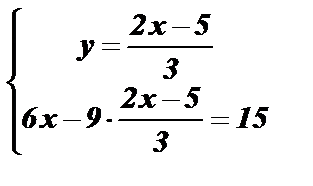
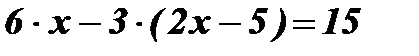 ;
; 
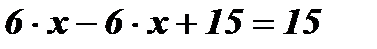 ; 15 = 15.
; 15 = 15.
Ответ:Система имеет бесконечное множество решений 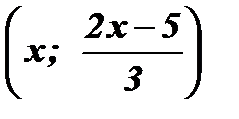
3) 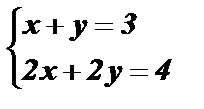 Û
Û 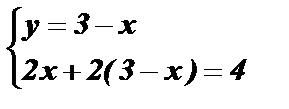
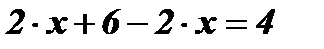 6
6 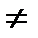 4
4
Дата добавления: 2016-09-06; просмотров: 2793;











