Геометрическая оптика 5 глава

Проанализируем выражения (23.19) и (23.20). Прежде всего при­мечательно, что решение уравнения Шредингера для электрона в потенциальной яме без каких-либо дополнительных постулатов приводит к дискретным, квантованным значениям энергии:

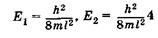и т. д.

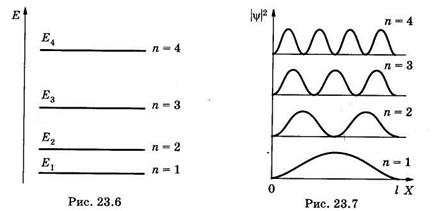
Энергетические уровни E₁ E₂, E₃, E₄, соответствующие раз­ным Состояниям электрона, схематически показаны на рис. 23.6. Вычислим разность энергий соседних уровней га + 1и га:

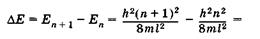
(23.21)

Из (23.21) видно, что при некотором фиксированном значении га дискретность, т. е. различие энергий соседних уровней тем меньше, чем больше размеры потенциальной ямы. Так, напри­мер, рассмотри два случая при га = 1:

Возведя (23.20) в квадрат, получим плотность вероятности нахождения электрона в разных точках потенциальной ямы. 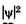На рис. 23.7 показана графическая зависимость от х при разных дискретных состояниях, т. е. разных квантовых 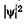числах. Как вид­но из рисунка, электрон может с разной вероятностью находиться в разных местах потенциальной ямы. Есть такие точки, в кото-

рых вероятность нахождения электрона вообще равна нулю. Это существенно отличается от представлений классической физики, согласно которым нахождение частицы в разных местах потенциальной ямы равновероятно (рис. 23.8), т. е. не­возможно разделение ямы точками, в ко­торых исключено нахождение частицы. Уравнение Шредингера можно применить и к более сложным силовым полям, например, к электрону в атоме. Это приведет к дополнительным математическим труднос­тям, но не изменит основных особенностей атомных систем: диск­ретности энергетических состояний, вероятностных суждений о нахождении электрона, своеобразной зависимости |\|/|² от коорди­нат и т. д.

§ 23.6. Применение уравнения Шредингера к атому водорода. Квантовые числа

Описание состояний атомов и молекул с помощью уравнения Шредингера является достаточно сложной задачей. Наиболее просто она решается для одного электрона, находящегося в поле ядра. Такие системы соответствуют атому водорода и водородопо-добным ионам (однократно ионизированный атом гелия, двукрат­но ионизированный атом лития и т. п.). Однако и в этом случае решение задачи выходит за рамки нашего курса, поэтому ограни­чимся лишь качественным изложением вопроса.

Прежде всего в уравнение Шредингера (23.13) следует подста­вить потенциальную энергию, которая для двух взаимодействую­щих точечных зарядов -е (электрон) и Ze (ядро), находящихся на расстоянии г в вакууме, выражается следующим образом:

(23.22)

При центральной симметрии поля, созданного ядром, удобнее решать задачу не в декартовых прямоугольных координатах, а в сферических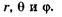

Решение уравнения Шредингера находят в виде произведения

функций:

(23.23)

Аналогично тому, как для электрона в прямоугольной потен­циальной яме с бесконечно высокими стенками граничные усло­вия привели к конкретным возможным значениям функции у и энергии Е_п, так и в потенциальной яме, соответствующей атому водорода, физические условия приводят к определенным типам функций f_v f₂, f₃ и, следовательно, y-функции. Здесь также про­является главная особенность квантово-механических систем — дискретность физических величин.

Дискретность математически проявляется в том, что любой из функций, являющейся решением уравнения Шредингера с задан­ными граничными условиями и потенциальной энергии Е_п, соот­ветствует набор (спектр) целочисленных значений параметров, каж­дому из которых отвечает так называемое квантовое число. В отли­чие от прямоугольной потенциальной ямы с бесконечно высокими стенками состояние электрона в атоме водорода характеризуется не одним, а несколькими квантовыми числами. Решением уравнения Шредингера вводятся три квантовые числа: п, l, т_l В общем случае квантовыми числами называют целые (0, ±1, ±2, ...) или полуце­лые (+1/₂, ±³/₂, ±⁵/2…) числа, определяющие возможные дискрет­ные значения физических величин, которые характеризуют кванто­вые системы.

Первое из них — главное квантовое число п = 1,2,3, ... . Оно определяет уровни энергии электрона в атоме водорода (z = 1) или водородоподобных ионах:

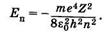
(23.24)

Это выражение вытекает из ре­шения уравнения Шредингера и полностью совпадает с соответст­вующей формулой теории Бора (см. §23.7).

На рис. 23.9 штриховыми пря­мыми показаны уровни возмож­ных значений полной энергии Е электронов в атоме водорода (E₁ Е₂, Е₃ и т. д.) и график зависимоcти потенциальной энергии Е_п от расстояния rмежду электроном и ядром [см. (23.22)]. С возрастанием главного квантового числа га увели­чивается r [см., например, (23.33)],

а полная [см. (23.24)] и потенциальная энергии стремятся к нулю. Кинетическая энергия также стремится к нулю. Заштрихованная область (Е > 0) — непрерывный спектр значений энергии — соот­ветствует состоянию свободного электрона.

Второе квантовое число — орбитальное квантовое число I, которое при данном п может принимать значения 0, 1, 2, ..., п — 1. Это число характеризует орбитальный момент импульса L_l элект­рона относительно ядра:

(23.25)

Третье квантовое число — магнитное квантовое число т_г, ко­торое при данном l принимает значения 0, ±1, +2, ..., ±1, всего 21 + 1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое произвольно выбранное направ­ление Z (или направление внешнего магнитного поля):

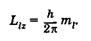(23.26)

Четвертое квантовое число — спиновое {магнитное спино­вое)¹ квантовое число m₈. Оно может принимать только два зна­чения (±¹/₂) и характеризует возможные значения проекции на ось Z спина (собственного механического момента) электрона:

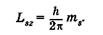(23.27)

Состояния электрона в атоме с заданными п и I обозначают сле­дующим образом: Is, 2s, 2p, 3s и т. д. Здесь цифра указывает зна­чение главного квантового числа, а буква — орбитальное кванто­вое число: символам s, p, d, f, ... соответствуют значения I =0, 1, 2, 3 и т. д. (табл. 30).

Число состояний с заданными п и I равно 2(2l + 1). Чтобы най­ти общее число состояний, имеющих одинаковое главное кванто­вое число, просуммируем 2(2l + 1) по всем возможным значениям l от l = 0 до l = п - 1:

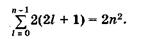(23.28)

Таким образом, первому уровню энергии атома водорода соот­ветствуют два состояния электрона, второму — 8, третьему — 18 и т. д. (см. табл. 30).

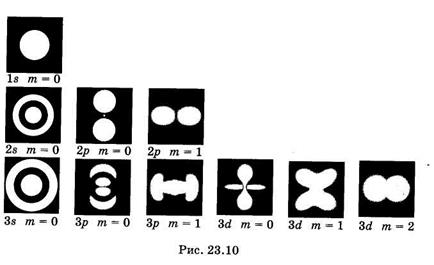
Наглядное представление о нахождении электрона в атоме да­ет фотомодель электронного облака (рис. 23.10). Снимки выпол­нены на модели со светящейся лампочкой. Рассчитав плотности вероятности нахождения электрона в атоме в состояниях с разными значениями п, l и m_l лампочку перемещали в соответст­вии с этим расчетом: больше времени она находилась в местах с большей плотностью вероятности, менее длительно — в местах с меньшей плотностью вероятности. В результате экспозиции на фотопленке получились места разной освещенности, которые ил­люстрируют распределение вероятности нахождения электрона в атоме. Из рисунков видно, сколь условно и даже неверно понятие «орбита» применительно к движению электрона.

Спиновый и орбитальный магнитные моменты взаимодейству­ют между собой, это изменяет систему энергетических уровней атома по сравнению с той, которая была бы без такого взаимодей­ствия. Спин-орбитальное взаимодействие приводит к расщепле­нию энергетических уровней и тонкой структуре спектральных линий излучения. Если это расщепление уровней существенно, то необходимо учитывать полный момент импульса электрона — ор­битальный плюс спиновый. При этом вместо тп₁ и m_s используют другие квантовые числа: j и т_j

Квантовое число j определяет дискретные значения полного момента импульса L_j. электрона:

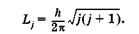(23.29)

При заданном l квантовое число у принимает два значения: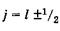

Таблица 30

i

Магнитное квантовое число т, характеризует возможные проекции полного момента импульса электрона L_j. на некоторое произвольно выбранное направление Z, либо направление внеш­него магнитного поля:

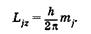(23.30)

При заданном у квантовое число т_j, принимает 2j + 1 значений: -j, -j + 1, ..., + j.

^{______________________}

¹ Наличие спина у частиц и спинового квантового числа не следует из уравнения Шредингера.

§ 23.7. Понятие о теории Бора

Еще до создания квантовой механики датский физик Н. Бор в 1913 г. предложил теорию атома водорода и водородоподобных ионов, которая основывалась на планетарной модели атома и двух постулатах. Постулаты Бора не укладывались в рамки классиче­ской физики.

Согласно первому постулату, атом и атомные системы могут длительно пребывать только в определенных стационарных со­стояниях. Находясь в таких состояниях, атом не излучает и не по­глощает энергии. Стационарным состояниям соответствуют диск­ретные значения энергии: E₁ Е₂, …..•

Любое изменение энергии атома или атомной системы связано со скачкообразным переходом из одного стационарного состояния в другое.

По второму постулату, при переходе атома из одного состояния в другое атом испускает или поглощает фотон частоты v, энергия которого определяется разностью энергий Е_j, E_k атомных состо­яний:

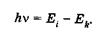(23.31)

Переход из состояния с большей энергией в состояние с мень­шей энергией сопровождается излучением фотона. Обратный про­цесс происходит при поглощении фотона.

Согласно теории Бора, электрон в атоме водорода вращается по круговой орбите вокруг ядра. Из всех возможных орбит стаци­онарные состояния соответствуют только тем, для которых мо­мент импульса (орбитальный механический момент) равен цело­му числу :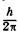

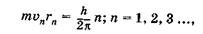(23.32)

где т — масса электрона, — его скорость на я-й орбите, r_n— ее радиус.

На электрон, вращающийся по круговой орбите в атоме (ионе), действует кулоновская сила притяжения со стороны положитель­но заряженного ядра, которая, по второму закону Ньютона, равна произведению массы электрона на центростремительное ускоре­ние (запись дана для вакуума):

(23.33)

где е — заряд электрона, Ze — заряд ядра. Для водорода Z = 1, для водородоподобных ионов Z > 1. Исключая ^{v n} из (23.32) и (23.33), получаем

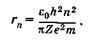(23.34)

Используя (23.33), находим кинетическую энергию электрона:

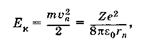(23.35)

а сумма кинетической (23.35) и потенциальной (23.22) энергий дает полную энергию электрона:

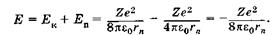(23.36)

Подставляя выражение (23.34) в (23.36), получаем дискретные значения энергии 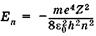, как в квантово-механическом описании атомов (23.24).

На основании второго постулата (23.31) и формулы (23.24) Бор получил формулу (24.14), объясняющую сериальные закономернос­ти спектра атома водорода и водородоподобных ионов (см. § 24.3).

Теория Бора в свое время явилась триумфом развития атомной физики. Впервые, хотя и для простейшей атомной системы (один электрон вращается вокруг ядра), были раскрыты закономернос­ти спектров.

Несмотря на большой успех теории Бора, скоро стали заметны и ее недостатки. Так, в рамках этой теории не удалось объяснить раз­личия интенсивностей спектральных линий, т. е. ответить на воп­рос, почему одни переходы между энергетическими уровнями бо­лее вероятны, чем другие. Теория Бора не раскрыла спектральных закономерностей более сложных атомных систем, в частности, ато­ма гелия (с двумя электронами, вращающимися вокруг ядра).

Недостатком теории Бора была ее внутренняя противоречи­вость. Эта теория объединяла в себе положения принципиально отличных теорий: классической и квантовой физики. Так, напри­мер, в соответствии с теорией Бора считается, что электрон в ато­ме движется по определенным орбитам (классические представле­ния), но при этом не излучает и не поглощает электромагнитной энергии (противоречит классической электродинамике).

В первой четверти двадцатого века стало ясно, что теория Бора должна быть заменена другой теорией атома, в связи с чем и по­явилась квантовая механика.

§ 23.8. Электронные оболочки сложных атомов

Квантовые числа, описывающие состояние электрона в атоме водорода, используют для приближенной характеристики состоя­ния отдельных электронов сложных атомов. Однако при этом следует учитывать по крайней мере два существенных отличия слож­ных атомов от атома водорода: 1) в сложных атомах энергия электронов из-за их взаимодействия зависит не только от п, но и от /; 2) распределение электронов по энергетическим уровням обусловлено принципом Паули, согласно которому в атоме не мо­жет быть двух (и более) электронов с четырьмя одинаковыми квантовыми числами.

При образовании электронной конфигурации, соответствую­щей невозбужденному состоянию атома, каждый электрон стре­мится иметь наименьшую энергию. Если бы не принцип Паули, то все электроны расположились бы на самом нижнем энергетиче­ском уровне. В действительности электроны последовательно заполняют состояния, которые указаны для атома водорода в табл. 30 (за некоторыми исключениями).

Электроны с одинаковым главным квантовым числом образу­ют слой. Слои обозначают буквами К, L, М, N и т. д. в соответст­вии с п = 1, 2, 3, 4, ... . Электроны, имеющие одинаковые пары значений n и l, входят в состав оболочки, которая кратко обозна­чается так же, как соответствующие состояния для электрона ато­ма водорода: 1s, 2s, 2р и т. д. Так, например, называют 2в-оболочка, 2в-электроны и т. п.

Число электронов в оболочке обозначают справа вверху около символической записи оболочки, например 2p⁴.

Распределение электронов по оболочкам в атоме (электронные конфигурации) обычно указывают следующим образом: для азота (Z = 7) — Is², 2s², 2р³; для кальция (Z = 20) — Is², 2s², 2р⁶, 3s², Зр⁶, 4s² и т. д.

Так как энергия электронов сложных атомов зависит не толь­ко от n, но и от l, то построение таблицы Менделеева не всегда происходит постепенным заполнением слоев по мере усложнения атома. У калия (Z = 19), например, вместо заполнения слоя М (что соответствовало бы конфигурации Is², 2s², 2p⁶, 3s², Зр⁶, 3d¹) начинается заполнение слоя N и создается следующая электрон­ная конфигурация: Is², 2s², 2р⁶, 3s², Зр⁶, 4s¹. Аналогичные откло­нения от «регулярного» заполнения слоев имеются и у некоторых других элементов.

Всегда выполняется общее правило: электроны невозбужден­ного атома занимают состояние с наименьшей энергией и в соот­ветствии с принципом Паули. На рис. 23.11 схематически без со­блюдения масштаба показаны энергетические состояния и уровни сложного атома и соответствующее им число электронов.

В заключение отметим, что состояние многоэлектронного атома в целом опреде­ляется следующими квантовыми числа­ми: L — квантовым числом полного орби­тального момента атома¹, которое прини­мает значения 0, 1, 2, 3 и т. д.; J — кванто­вым числом полного момента атома, которое может принимать значения с ин­тервалом в единицу от \L - S\ до L + S; S — квантовым числом результирующего спи­нового момента атома; магнитным кванто­вым числом то,, которое определяет диск­ретные значения проекции полного момен­та импульса атома L_A на некоторую ось Z:

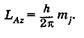(23.37)

При заданном J квантовое число т.- при­нимает 2J+ 1 значений: -J, -J +1, ..., +J.

§ 23.9. Энергетические уровни молекул

Энергетические уровни молекул имеют более сложное стро­ение, чем у атомов. Это вызвано тем, что в молекуле, кроме дви­жения электронов относительно ядер, происходит колебательное движение атомов около их положения равновесия (колебание ядер вместе с окружающими их электронами) и вращательное движение молекулы как целого.

Электронному, колебательному и вращательному движени­ям молекулы соответствуют три типа уровней энергии: Е_эл, Е_кол и Е_вр.

Согласно квантовой механике, энергия всех видов движения в молекуле принимает только дискретные значения (квантуется). Полная энергия Е молекулы может быть представлена суммой квантованных значений энергии разных видов:

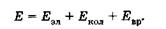(23.38)

На рис. 23.12 схематически изображена система уровней молеку­лы! далеко отстоящие электронные уровни энергии а' и а", для кото­рых Е_кол = Е_вр = 0; более близко расположенные колебательные уровни v' и v", для которых Е_вр = 0; наиболее тесно расположенные вращательные уровни J' и J" с различными значениями Е .

«Расстояние» между электронными уровнями энергии пример­но 1—10 эВ, между соседними колебательными уровнями — 10 ^-2— 10 ^-1 эВ, между соседними вращательными уровнями — 10 ^-5—10 ^-3 эВ.

Квантование колебательной энергии двухатомной молекулы можно объяснить, если рассматривать молекулу как гармониче­ский осциллятор. Допустим, что атомы сопротивляются смеще­нию из положения равновесия с силой 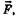пропорциональной вели-

чине смещения х, тогда, следуя закону Гука (см. § 5.1), можно написать выражение для частоты колебаний двухатомного ос­циллятора (вибратора)

(23.39)

где k — является мерой «упругости», или силы химической связи между атомами. Чем выше упругость или меньше масса ато­мов, тем выше частота колебаний.

На основании (5.25) можно написать вы­ражение для потенциальной энергии ос­циллятора

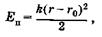(23.40)

где (г - г₀) — смещение относительно поло­жения равновесия. Подставив (23.40) в уравнение Шредингера (23.14), получим

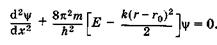(23.41)

Решение уравнения (23.41) дает выраже­ние для полной энергии колебаний Е_кол

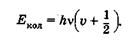(23.42)

Величина v — колебательное квантовое чис­ло, которое может принимать значения 0, 1, 2, ...и т. д.

При аппроксимации двухатомной молекулы моделью гармони­ческого осциллятора график зависимости потенциальной энергии (23.40) от межатомного расстояния (рис. 23.13) представляет собой параболу с равноотстоящими уровнями колебательной энер­гии. Горизонтальные кривые соответствуют Е_кол — полной энер­гии (кинетическая плюс потенциальная) вибратора на колебатель­ных уровнях, характеризуемых значениями v = 0, 1, 2 и т. д.

Интересно, что даже на нижнем колебательном уровне (и = 0) в точке г = г₀, соответствующей положению равновесия, молекула обладает половиной кванта колебательной энергии (см. рис. 23.14). Для молекулярного водорода это составляет 0,269 эВ. Молекула со­храняет такую колебательную энергию даже при абсолютном нуле.

Рассмотрим молекулу с колебательным уровнем v = 2 и перво­начально находящуюся в состоянии сжатия (в точке С, межъядер­ное расстояние r_c). Тогда вся энергия будет потенциальной, и ки­нетическая энергия осциллятора равна нулю. Такая молекула мо­жет колебаться между точками С и С. В точке r= г₀ кинетическая энергия будет достигать максимума, а потенциальная будет рав­няться нулю.

Используя приближение классического осциллятора, можно предсказать, что максимальное смещение при колебательном дви­жении соответствует двум точкам поворота С и С и что осциллятор должен находиться большую часть времени вблизи этих точек. Квантовая механика также предсказывает значения наибольшей плотности вероятности нахождения атомов в областях вблизи то­чек поворота, но значительно смещенных к центру (межъядерное расстояние г₁). Это показано на рис. 23.13, где распределение плотности

вероятности 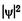представлено для колебательных уровней двухатомной молекулы в зависимости от расстояния г меж­ду томами молекулярного гармонического осциллятора. Вместо простой классической картины с двумя максимумами вероятнос­ти (в точках А и А', В и В', С и С’) рис. 23.13 дает 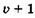максиму­мов. При этом на нижнем колебательном уровне наиболее вероят­но нахождение молекулы в положении r₀, а на более высоких уровнях — ближе к областям точек поворота.

Модель гармонического осциллятора удовлетворительно опи­сывает колебание двухатомной молекулы лишь при небольших смещениях r - r₀, тогда как разрыв химических связей происхо­дит при значительных смещениях ядер. Реальные кривые потен­циальной энергии асимметричны, как это показано на рис. 23.14 на примере молекулы водорода. Гармонический осциллятор пред­сказывает серию равноотстоящих уровней колебательной энер­гии, однако в действительности (при асимметрии потенциальной кривой) уровни сгущаются с ростом и. В пределе, когда энергия колебаний становится равной энергии связи, дискретные уровни сливаются, и для энергий, превышающих энергию связи, получа­ется сплошной спектр значений. Это означает, что при таких энергиях связь разрывается и атомы разлетаются с определенной относительной скоростью, соответствующей данному значению энергии в области сплошного спектра.

Существенный результат квантово-механических расчетов за­ключается в том, что в самом нижнем колебательном состоянии (v = 0) осциллятор обладает энергией так называемых нулевых

колебаний . Классическое же решение задачи допускает реше­ния, соответствующие покоящемуся осциллятору с энергией, рав­ной нулю: такое состояние отвечало бы наличию определенной координаты г₀ и определенной скорости, равной нулю, что проти­воречит соотношениям неопределенностей.

В биологии и медицине особенно важны представления об энергетических состояниях сложных органических молекул, со­держащих двойные ковалентные связи между атомами углерода.

Одинарную связь между атомами углерода образуют s-электроны (s-связь), в ее формировании участвуют два электрона с про­тивоположными спинами (спаренные электроны). Они формиру­ют единое вытянутое электронное облако, симметричное относи­тельно прямой, соединяющей центры атомов. На рис. 23.15, а показаны s-связи между атомами углерода в n-гексане. Области перекрывания заштрихованы, они находятся в промежутках между атомами, s-орбитали соседних одинарных связей не пере­крываются друг с другом.

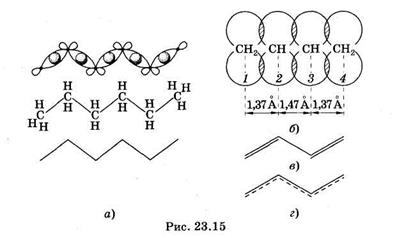
При возникновении между атомами углерода второй связи происходит перекрывание орбиталей еще двух электронов (р-орбиталей) соседних углеродных атомов. Их электронные облака имеют в сечении вид восьмерки, ось которой перпендикулярна направлению s-связи. Боковое перекрывание этих орбиталей в двух областях приводит к образованию молекулярной p-орбитали (рис. 23.15, б), соответственно электроны, формирующие p-орби-таль, называют p-электронами. Плотность образовавшегося обла­ка л-электронов сосредоточена по обеим сторонам от линии s-связи. Она максимальна на расстоянии примерно 1 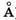(10~¹⁰ м) от ли­нии s-связи и обращается в нуль вблизи ядер атомов. Если двойные связи разделены одной одинарной (сопряжены), то про­исходит перекрывание p-орбиталей всех атомов углерода, участ­вующих в образовании цепочки сопряженных связей. На рис. 23.15, б показаны перекрывающиеся p-орбитали атомов углерода в молекуле бутадиена, одинарные s-связи условно изображены прямыми линиями, соединяющими атомы углерода. Данные о длине связей в молекуле бутадиена указывают на то, что при со­пряжении двойных связей нет обычных двойных (длина связи

1,33 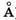) или одинарных (1,54 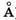) связей, связи являются примерно полуторными. Поэтому, хотя в органической химии и принято изображать систему сопряженных двойных связей, как показано на рис. 23.15, в, более точно ситуацию отображает рис. 23.15, г. Каждый электрон, участвующий в образовании двойной связи, оказывается принадлежащим не какой-то определенной паре ато­мов углерода, а сразу всей цепочке атомов, связанных сопряжен­ными связями. Такие p-электроны делокализованы по всей цепочке и могут свободно по ней перемещаться подобно электронам проводимости в металле, но не могут ее покинуть. Другими слова­ми электроны p-орбиталей находятся в потенциальной яме. Мож­но показать, что энергия этих электронов квантована, подобно энергии электронов в атоме.

Представим, что сопряженная цепь состоит из N звеньев, включающих по одной двойной и одной одинарной связи, тогда общая длина цепи равна

I = NL, (23.43)

где L — длина одного звена. Квантование энергий p-орбиталей яв­ляется следствием волновых свойств электронов (23.2). Электрон (волна) перемещается по потенциальной яме длиной I со скоро­стью v, не выходя за ее пределы. Внутри ямы вся энергия электро­на кинетическая, на краях ямы — потенциальная. Волна будет устойчива, если внутри ямы укладывается целое число п полу­волн, т. е. если волна будет стоячей с узлами на стенках