Геометрическая оптика 2 глава

Оптической системе глаза свойственны некоторые специфиче­ские недостатки.

В нормальном глазу при отсутствии аккомодации задний фо­кус совпадает с сетчаткой — такой глаз называют эмметропическим; глаз называют аметропическим, если это условие не вы­полняется.

Наиболее распространенными видами аметропии являются близорукость (миопия) и дальнозоркость (гиперметропия). Близорукость — недостаток глаза, состоящий в том, что задний фокус при отсутствии аккомодации лежит впереди сетчатки; в случае дальнозоркости задний фокус при отсутствии аккомода­ции лежит за сетчаткой. Для коррекции близорукого глаза при­меняют рассеивающую линзу, дальнозоркого — собирающую.

¹ Это вопрос не только физический, но и физиологический.

§ 21.6. Лупа

Возможность разрешения деталей предмета зависит от размеров его изображения на сетчатке глаза или от угла зрения. Угол зрения можно увеличить, приблизив предмет к глазу, однако это связано с некоторыми ограничениями: 1) в ряде случаев технически невоз­можно существенно изменить расстояние между предметом и гла­зом (например, при рассмотрении звезд или Солнца); 2) невозмож­но приблизить предмет на расстояние меньшее, чем до ближней точки глаза, из-за предельных возможностей аккомодации.

В связи с этим для увеличения угла зрения используют оптиче­ские приборы: телескопы, лупы, микроскопы и т. п.

Рассмотрим устройство одного из наиболее простых оптиче­ских приборов — лупы.

Лупой называют оптическую систему, в передней фокаль­ной плоскости которой или в непосредственной близости от нее расположен наблюдаемый предмет.

Изображение, создаваемое лупой, находится в бесконечности или на удобном для глаза расстоянии. Если изображение в беско­нечности, то оно наблюдается глазом без аккомодации.

На рис. 21.14, а показано двумя лучами, как с помощью лупы формируется изображение на сетчатке; N — объединенная узловая точка оптической системы глаза, предмет помещен в передней фо­кальной плоскости. Луч 1 проходит через центр лупы без преломле­ния, а затем преломляется глазом. Другие лучи, идущие от этой же

точки предмета, после преломления в лупе будут параллельны лучу 1. Чтобы определить положение изображения на сетчатке, выберем из этих лучей тот, который проходит через объединенную узловую точку (луч 2). Он не преломляется глазом. Его пересечение с сетчат­кой и укажет положение изображения предмета. Остается лишь для полноты картины достроить начальную часть луча 2 и конечную часть луча 1 (показаны штриховыми линиями).

Увеличением лупы называют отношение угла зрения 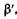под которым видно изображение предмета (см. рис. 21.14, а), к углу зрения 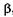, под которым виден предмет, находящийся на расстоя­нии наилучшего зрения а₀ = 25 см (рис. 21.14, б).

Из рисунков видно:

(21.10)

где В — линейный размер предмета. Учитывая (21.10), получаем увеличение лупы

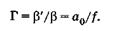(21.11)

Отсюда видно, что формула для увеличения связывает посто­янную величину фокусного расстояния f лупы с расстоянием на­илучшего зрения — довольно условной величиной. У близорукого глаза а₀ < 25 см, у дальнозоркого а₀ > 25 см, поэтому для близору­кого глаза увеличение от одной и той же лупы будет меньше, чем для дальнозоркого.

Учитывая, что напряжение аккомодации сильно утомляет глаз и допустимо лишь как кратковременное явление, следует при пользовании лупой помещать предмет в фокальную плоскость, а глаз — у самой лупы.

Лупы изготовляют из одной или нескольких линз. Увеличение лупы зависит от ее конструкции и изменяется в пределах от 2 до 40—50. Наиболее распространены лупы с 10-кратным увеличением.

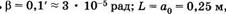
Разрешаемое с помощью лупы расстояние между двумя точками мож­но вычислить по формуле (21.8). Например, если для 10-кратного увели­чения взять,

то получим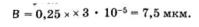

§ 21.7. Оптическая система и устройство микроскопа

Для получения больших увеличений в качестве лупы следует использовать [см. (21.11)]короткофокусные линзы. Однако такие линзы имеют небольшие размеры, им свойственны значительные

аберрации, что накладывает ограничения на увеличение лупы. Большее увеличение можно осуществить, рассматривая действи­тельное изображение предмета, созданное дополнительной лин­зой или системой линз. Таким оптическим устройством является микроскоп; лупу в этом случае называют окуляром, а дополни­тельную линзу или систему линз — объективом.

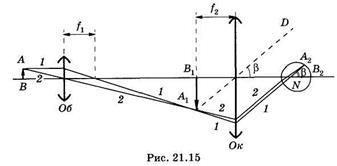
Для того чтобы глаз не был напряжен, стремятся совместить изображение, созданное объективом, с фокальной плоскостью окуляра. На рис. 21.15 показан ход лучей в микроскопе, объекти­вом и окуляром которого являются собирающие линзы, и в глазу.

Изображение А₁В₁ предмета АВ, созданное линзой объектива Об, находим согласно правилу построения изображения в тонкой линзе; луч 1, параллельный главной оптической оси, проходит после преломления в линзе через фокус, луч 2 через центр линзы идет без преломления; изображение А1В₁ расположено в передней фокальной плоскости окуляра.Лучи 1 и 2 доходят до линзы окуляра Ок и в ней преломляют­ся. Чтобы показать ход этих лучей после преломления в окуляре, проведем следующее рассуждение.

Все лучи, идущие из некоторой точки фокальной плоскости (например, A1, после преломления в линзе должны распростра­няться параллельно друг другу. Проведем из А₁ луч A1D через центр линзы; лучи 1 и 2 после преломления в окуляре пройдут па­раллельно A_tD до встречи с глазом. Пусть луч 1 проходит через объединенную узловую точку N глаза и потому без преломления дойдет до точки А₂ сетчатки. В эту же точку сфокусируется луч 2. На сетчатке глаза получаем изображение А₂В₂ предмета АВ.

В современных оптических микроскопах объектив и окуляр состоят из нескольких линз, представляющих собой единую

центрированную оптическую систему (рис. 21.16). Главные плоскости объектива и окуляра такой системы показаны на ри­сунке раздельно, окружающая среда имеет одинаковый показа­тель преломления. Лучи 1 и 2, идущие от точки В предмета АВ, пересекаются в точке В', где формируется изображение, создавае­мое объективом. Луч 2 попадает на окуляр параллельно главной оптической оси, поэтому он проходит через фокус F'₂. Так как лу­чи 1 и 2 выходят из одной точки В' фокальной плоскости, то после преломления в окуляре они будут параллельны друг другу.

Можно указать главные точки и фокусы микроскопа как еди­ной центрированной оптической системы. Так как луч 1 в про­странстве предметов параллелен главной оптической оси, то он в пространстве изображений пересечет оптическую ось в заднем фо­кусе F'. Главные точки и плоскости найдем из условия, что точка и ее изображение, расположенные в соответствующих главных плоскостях, равноудалены от главной оптической оси.

Чтобы не загромождать чертеж, выберем точку К передней главной плоскости так, чтобы луч, распространяющийся от этой точки параллельно оптической оси, в пространстве предметов сов­падал с лучом 1. Сопряженную ей точку К', расположенную в за­дней фокальной плоскости, найдем из условия, что она лежит на луче 1 и удалена на такое же расстояние от главной оптической оси, как и точка К. Проецируя К' на главную оптическую ось, по­лучаем заднюю главную точку Н'.

Для нахождения передней главной точки из К' направим луч 3 параллельно главной оптической оси. Он пройдет через F₂ до пе­ресечения с задней главной плоскостью объектива. Чтобы опре­делить направление этого луча после выхода из передней глав­ной плоскости объектива, сделаем дополнительное построение: из

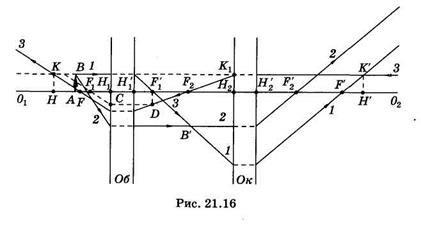
точки D, лежащей в фокальной плоскости, проводим луч DC па­раллельно главной оптической оси, он должен пройти через фокус F1 а луч 3 пройдет параллельно CF_V Пересечение луча 3 с глав­ной оптической осью дает передний фокус F микроскопа, а с лу­чом 1 — положение точки К, которая лежит в передней главной плоскости; Н — передняя главная точка микроскопа.

Отметим, что в этом случае фокусы расположены между глав­ными точками.

Так как показатели преломления среды пространств предмета и изображения одинаковы, то на основании (21.6) фокусные рас­стояния равны между собой: / = —f.

Определим фокусное расстояние микроскопа.

Из подобия 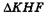и 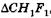, а также 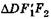и соответственно имеем

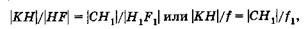(21.12)

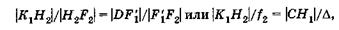(21.13)

где f₁ — фокусное расстояние объектива, f₂ — фокусное расстоя­ние окуляра, — расстояние между задним фокусом объектива и передним фокусом окуляра, называемое оптической длиной тубуса. Разделив (21.12) на (21.13) и учитывая, что \КН\ = \К_гН₂\, имеем f₂: f = : f1 откуда фокусное расстояние микроскопа

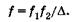(21.14)

Так как и для микроскопа в принципе справедлива общая фор­мула (21.11), то [см. (21.14)]

(21.15)

Итак, увеличение микроскопа равно отношению произведения оптической длины тубуса на расстояние наилучшего зрения а₀ к произведению f_lf₂ фокусных расстояний объектива и окуляра. Формулу (21.15) можно представить как произведение двух

сомножителей:

(21.16)

где Г_ок — увеличение окуляра, Г_об — увеличение объектива¹.

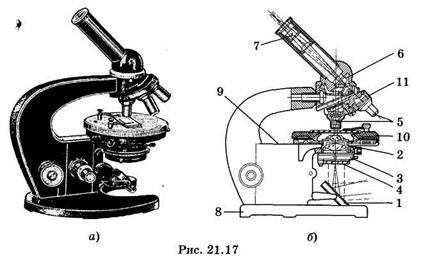
На рис. 21.17 изображены общий вид (а) и схема (б) биологиче­ского микроскопа. Его главные части: основание 8, коробка с мик­рометрическим механизмом 9, предметный столик 10, револь­вер 11с объективами 5, конденсор 2 и окуляр 7. Оптическая сис­тема состоит из двух частей: осветительной и наблюдательной. В осветительную часть входят зеркало 1, конденсор с ирисовой апертурной диафрагмой 3 и съемный светофильтр 4, а в наблюда­тельную — объектив, призма 6 и окуляр, соединенные в тубусе микроскопа.

Пучок лучей от источника света падает на зеркало, которое от­ражает его к диафрагме, проходит через конденсор и исследуе­мый препарат и затем попадает в объектив.

§ 21.8. Разрешающая способность и полезное увеличение микроскопа. Понятие о теории Аббе

Из формулы (21.15) можно сделать вывод, что при надлежа­щем выборе f1 и f₂ увеличение микроскопа будет сколь угодно большим. Однако на практике биологи, врачи и другие спе­циалисты, работающие с микроскопами, редко используют уве­личения, превышающие 1500—2000. Чтобы уяснить причины такого положения, ознакомимся с понятиями «предел разреше­ния», «разрешающая способность» и «полезное увеличение мик­роскопа».

Предел разрешения — это такое наименьшее расстояние между двумя точками предмета, когда эти точки различи­мы, т. е. воспринимаются в микроскопе как две точки.

Разрешающей способностью обычно называют способность микроскопа давать раздельные изображения мелких деталей рассматриваемого предмета. Это величина обратна пределу раз­решения. Разрешающая способность микроскопа обусловлена вол­новыми свойствами света, поэтому выражение для предела разре­шения можно получить, учитывая дифракционные явления.

Рассмотрим дифракционную теорию разрешающей способнос­ти микроскопа, предложенную Э. Аббе.

При освещении прозрачного предмета в микроскоп попадает свет, рассеянный (дифрагированный) объектом. В качестве наибо­лее простого предмета была взята дифракционная решетка — объ­ект с достаточно определенной структурой.

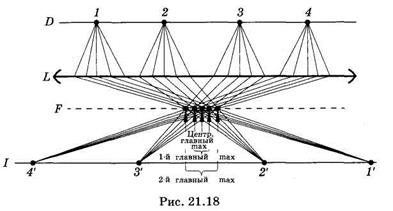
Пусть решетка D (рис. 21.18) состоит из четырех щелей 1—4. От каждой щели распространяются вторичные волны, на рисунке показан ход пяти лучей от каждой такой волны. Вторичные вол­ны, падающие под одинаковым углом к оптической оси линзы L, соберутся в фокальной плоскости F. Если разность хода вторич­ных волн, идущих от соседних щелей и отклоненных на одинако­вый угол, равна целому числу длин волн, то в местах, обозначен­ных точками на плоскости F, появятся главные максимумы (центральный, 1-й, 2-й). Картину, образуемую в фокальной плос­кости линзы, называют первичным изображением. Оно содержит определенную информацию о предмете, однако не является изо­бражением в общепринятом понимании.

Собственно изображение, или вторичное изображение (1'—4', образуется в плоскости I при пересечении вторичных волн, иду­щих от каждой из щелей. Вторичное изображение создается после первичного, поэтому оно не может содержать большей информации о предмете, чем первичное.

В оптических устройствах, в том числе и в микроскопе, пучки света всегда ограничены, поэтому важно знать, к какому искаже­нию изображения предмета это может привести и какое мини­мальное количество лучей способно передавать правильную ин­формацию о предмете.

Главные максимумы попарно симметрично располагаются от­носительно центрального и в некоторой степени дублируют друг друга. Совокупность максимумов, расположенных с одной сторо­ны от центра, вместе с центральным достаточна, чтобы передать информацию о предмете. Следовательно, экранирование лучей, идущих от максимумов, расположенных по другую сторону от центра, лишь уменьшит яркость изображения предмета.

При экранировании в плоскости F лучей от нечетных главных максимумов объективно создаются условия, при которых второй главный максимум играет роль первого, четвертый — второго, и т. д., и, как видно из (19.29), изображение будет такое же, как и у дифракционной решетки с вдвое меньшим периодом.

Центральный максимум имеет общую структуру для решеток с разным периодом и, следовательно, не содержит информации об особенностях предмета. Поэтому если пропустить лучи только центрального максимума, экранировав все остальные, то вторич­ное изображение предмета (решетки) не сформируется.

Такого рода опыты с различным ограничением пучков света в плоскости F проделал Аббе. Он установил, что для соответствия вторичного изображения предмету необходимо по крайней мере, чтобы из первичного изображения проходили дальше лучи цент­рального и одного из первых главных максимумов.

Реально свет от предмета распространяется к объективу мик­роскопа в некотором конусе (рис. 21.19, а), который характеризуется угловой апертурой —

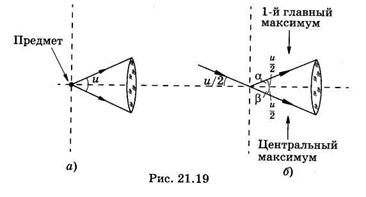
углом и между крайними лучами конического светового пучка, входящего в оптическую систему¹. В предельном случае, согласно Аббе, крайними лучами кониче­ского светового пучка будут лучи, соответствующие центрально­му (нулевому) и 1-му главному максимумам (рис. 21.19, б). При этом луч падает на предмет (решетку) под углом и/2, такой же угол и для первого дифракционного максимума. Из формулы (19.39) при = u/2 и 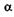= -и/2 получаем

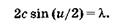(21.17)

В рассмотренной модели предмета (решетка) за предел разре­шения г следует принять элемент структуры — постоянную диф­ракционной решетки с, т. е. z = с при указанных а и 3. Из (21.17)

находим

(21.18)

или, учитывая, что 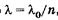, и вводя А = п sin (и/2),

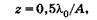(21.19)

где А — числовая апертура, п — показатель преломления сре­ды, находящейся между предметом и линзой объектива,^l0— длина волны света в вакууме.

Как видно из формулы (21.19), один из способов уменьшения предела разрешения микроскопа — использование света с мень­шей длиной волны. В связи с этим применяют ультрафиолетовый микроскоп, в котором микрообъекты исследуются в ультрафиоле­товых лучах. Принципиальная оптическая схема такого микро­скопа аналогична схемам обычного микроскопа. Основное отли­чие заключается, во-первых, в использовании оптических уст­ройств, прозрачных для ультрафиолетового света, и, во-вторых, в особенности регистрации изображения. Так как глаз непосредст­венно не воспринимает этого излучения, то употребляются фото­пластинки, люминесцентные экраны или электронно-оптические преобразователи (см. раздел седьмой).

Другой способ уменьшения предела разрешения микроскопа — увеличение числовой апертуры, что достигается увеличением как показателя преломления среды между предметом и объективом, так и апертурного угла. В обычных условиях (воздух) показатель преломления равен единице. Угол же и/2 может иметь большие значения — теоретически до 90°. Если этот угол очень велик, то лу­чи первого максимума могут не попасть в объектив. Так, например,

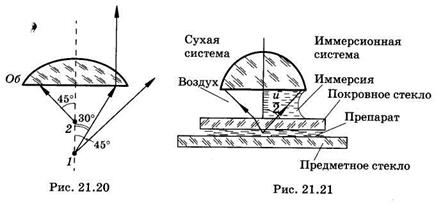
на рис. 21.20 показано, что объектив Об не захватывает лучей, вы­ходящих из точки 1 под углом 45°. Чтобы эти лучи попали, надо предмет приблизить к объективу, например в точку 2. Однако рас­стояние предмета от линзы не может изменяться произвольно, оно постоянно для каждого объектива и приближать предмет нельзя.

Числовая апертура может быть увеличена с помощью специаль­ной жидкой среды — иммерсии — в пространстве между объекти­вом и покровным стеклом микроскопа. В иммерсионных системах по сравнению с тождественными «сухими» системами получают больший апертурный угол (рис. 21.21). В качестве иммерсии ис­пользуют воду (п — 1,33), кедровое масло (п = 1,515), монобромнафталин (п = 1,66) и др. Для каждой иммерсии специально рассчиты­вают объектив, и его можно применять только с данной иммерсией.

В современных микроскопах угол и/2 достигает наибольшего значения, равного 70^е. С этим углом получают максимальные чис­ловые апертуры и минимальные пределы разрешения (табл. 28).

Таблица 28

A Z' мкм Сухая система 0,94 • 1 = 0,94 0,30 Водяная иммерсия 0,94 • 1,33 = 1,25 0,22 Масляная иммерсия 0,94 • 1,515 = 1,43 0,19

Данные приведены для наклонного падения света на объект и наибо­лее чувствительной глазу длины волны 0,555 мкм.

Условия освещения объекта влияют на разрешающую способ­ность микроскопа, что важно учитывать в биологических исследо­ваниях. Известен курьез, когда исследователи-биологи отнесли к

разным видам диатомею, так как разные условия освещения выявляли иначе структуру её панциря. На рис. 21.22 показан вид объекта при полном (а) и частичном (б) разрешении из-за разного освещения.

Заметим, что окуляр совершенно не влияет на разрешающую способность мик­роскопа, он только создает увеличенное изображение объектива.

Оценим полезное увеличение микро­скопа, используя формулу (21.19).

Если предмет имеет размер, равный пределу разрешения z, а размер его изо­бражения г', и если это изображение рас­положено на расстоянии наилучшего зре­ния от глаза, то увеличение микроскопа Г = г'/г.

Подставляя в эту формулу 2 из (21.19), получаем

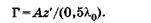(21.20)

Нормальный глаз в предельном случае различает две точки предме­та, угловое расстояние между которыми равно 1' (см. § 21.4). Счита­ют, что удобная различимость должна соответствовать углу зрения в интервале от 2' до 4' или значениям z' (на расстоянии наилучшего зрения) от 140 до 280 мкм. Подставляя их, а также = 0,555 мкм f в формулу (21.20), находим интервал значений увеличения мик­роскопа:

500А<Г<1000А.

Эти увеличения называют полезными, так как при них глаз различает все элементы структуры объекта, которые разрешимы микроскопом.

Подставляя числовую апертуру иммерсионной системы с мас­лом (А = 1,43) в (21.21), получаем следующее неравенство для по­лезных увеличений такого микроскопа: 700 < Г < 1400.

¹ Предполагается, что объектив микроскопа наиболее сильно ограни­чивает световой поток, т. е. является апертурной диафрагмой.

§ 21.9. Некоторые специальные приемы оптической микроскопии

Измерение размеров микроскопических объектов с по­мощью микроскопа.Для этого применяют окулярный микро­метр — круглую стеклянную пластинку, на которой нанесена шкала с делениями. Микрометр устанавливают в плоскости изо бражения, получаемого от объекти­ва. При рассматривании в окуляр изображения объекта и шкалы на­кладываются и можно отсчитать, ка­кое расстояние по шкале соответст­вует измеряемой величине. Отсчет по шкале еще не дает размера объекта, так как совмещаемое со шкалой изо­бражение не равно размеру предмета. Надо найти цену одного деления оку­лярного микрометра, для этого при-

меняют объектный микрометр — шкалу с делениями по 0,01мм. Рассматривая объектный микрометр как предмет, совмещают в одном поле зрения две шкалы — объектную и окулярную — и оп­ределяют цену деления окулярного микрометра.

Вместо объектного микрометра можно применить любой пре­парат, размер которого известен, или использовать счетную каме­ру Горяева, употребляемую в медицинских измерениях.

В настоящее время широко применяют окулярно-винтовой мик­рометр, который изображен на рис. 21.23. Этот прибор устанавлива­ют вместо окуляра. При вращении винта перемещается перекрес­тие, что позволяет отсчитывать доли делений микрометра. Окуляр­но-винтовой микрометр нуждается в предварительной градуировке. Микропроекция и микрофотография.Формирование мик­роскопического изображения происходит с участием человека и завершается образованием действительного изображения в глазу. Обычный микроскоп сам по себе не создает действительного изо­бражения, однако для фотографирования (микрофотография) или проекции микроскопического изображения на экран (микропро­екция) должно быть получено действительное изображение. Для этого изображение, даваемое объективом Об, надо расположить дальше фокусного расстояния окуляра Ок (рис. 21.24).

Метод фазового контраста.Интенсивность световой волны, проходящей через прозрачный объект, почти не изменяется, но фазы претерпевают изменения, зависящие от толщины объекта и его показателя преломления. В этом смысле прозрачные объекты называют дефазирующими. Увидеть детали таких объектов обычным образом невозможно. В биологических исследованиях такие объекты иногда окрашивают, однако при этом могут изме­няться их свойства и жизнеспособность.

Для рассмотрения деталей дефазирующих объектов Ф. Цернике предложил метод фазового контраста.

Пусть объект состоит из однородной прозрачной среды 1 с по­казателем преломления п, в которой имеется прозрачное включе­ние 2, например бактерия с показателем преломления п₁ (рис. 21.25). При попадании плоскопараллельного пучка света часть его будет проходить через прозрачный объект и линзой L фокуси­роваться в небольшом участке Ф фокальной плоскости F, а другая часть будет дифрагировать на неоднородности и соберется линзой в точке А плоскости I.

Фазовый состав световых колебаний в плоскости I графически в координатах интенсивность—фаза изображен на рис. 21.26. Кривая 1 соответствует прямому свету, прошедшему через объект без дифракции, кривая 2 — свету, дифрагированному объектом.

Если п1 > п₂, то эта кривая будет от­ставать по фазе, что и показано на ри­сунке. Кривую 2 можно представить как сумму двух волн. Одна из них (1) проходит объект без дифракции, дру­гая (3) является результатом дифрак­ции на бактерии с показателем прелом­ления n1. Кривую 3 можно найти гра­фически, вычитая из ординат кривой 2 ординаты кривой 1.

Глаз в плоскости I (см. рис. 21.25) не различает волны 1 и 2, так как их интенсивности одинаковые, а на различие фаз глаз не реаги­рует; Необходимо фазовый рельеф преобразовать в амплитудный.

Как видно из рис. 21.26, волна 3 сдвинута по фазе относитель­но волны 1 приблизительно на 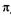/2, что соответствует оптической разности хода /4. Если изменить фазу волны 1 на 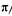'2, то волны 1 и 3 окажутся либо в фазе (рис. 21.27, а), либо в противофазе (рис. 21.27, б). Кривую 2 найдем графически как сумму ординат кри­вых 1 и 3. Из рисунка видно, что в этом случае волны 1 _и 2 уже различаются по интенсивности (амплитуде), поэтому глаз заметит бактерию на однородном световом поле.

Так как волна 1 проходит в плоскости F (см. рис. 21.25) через не­большой участок, то можно, поставив в этом месте небольшую круг­лую пластинку (фазовую пластинку) Ф, изменить фазу волны. Иногда фазовую пластинку изготавливают из материала, который частично поглощает волну 1, в этом случае контраст изображения бактерии бу­дет еще сильнее, так как будет увеличена разница амплитуд волн 1 и 2. Фазово-контрастные устройства (пластинки, конденсоры) обычно комплектуют как дополнительные приспособления к микроскопам.

Ультрамикроскопия.Это метод обнаружения частиц, разме­ры которых лежат за пределами разрешения микроскопа. Микро­скопы, работающие по этому методу, называют ультрамикроско­пами. В них осуществляют боковое (косое) освещение, благодаря чему субмикроскопические частицы видны как светлые точки на темном фоне; строение частиц увидеть нельзя.