Электронный осциллограф

<79 80 818283 84 85 >

Осциллограф — это измерительное устройство для визуального наблюдения или записи функциональной зависимости двух ветчин, преобразованных в электрический сигнал. Осциллографы (широко используют для наблюдения временной зависимости переменной величины.

Главной частью электронного осциллографа является электронно-лучевая трубка (ЭЛТ), показанная на рис. 18.17. Ее элементы расположены в вакуумированном баллоне Б. Они включают в себя люминесцирующий экран Э, отклоняющую систему О из двух пар отклоняющих пластин и электронную пушку П (выделена штриховой линией), состоящую из подогревного катода, подобного катоду диода, и специальных электродов, которые ускоряют и фокусируют электроны. На пластины вертикального и горизонтального отклонения подается разность потенциалов. В зависимости от ее знака и значения пучок электронов отклоняется в вертикальном или горизонтальном направлении. Сформированный и определенным образом направленный электронный пучок попадает на люминесцирующий экран — переднюю стенку электронно-лучевой трубки, покрытую люминофорами, которые способны светиться под воздействием ударов электронов (катодолюминесценция).

Пучок электронов на экране изобразится светящейся точкой. Плавно изменяя напряжение на отклоняющих пластинах, светящуюся точку можно перемещать по экрану. Люминофоры обладают свойством послесвечения, они светятся в данном месте некоторое время после того, как электронный пучок сместился с данного места. Поэтому перемещение пучка наблюдается на экране в виде линии.

Структурная схема осциллографа дана на рис. 18.18: У_х и У_у — усилители, БП — блок питания, ГР — генератор развертки, ЭЛТ — электронно-лучевая трубка. Имеется также блок синхронизации. На рис. 18.19 изображена передняя панель осциллографа.

Поданный на клеммы «Вход Y» и «Земля» сигнал усиливается и подается на вертикально отклоняющие пластины. На экране осциллографа такой сигнал изобразится отрезком вертикальной прямой.

Для наблюдения зависимости сигнала от времени следует светящейся точке сообщить одновременно равномерное движение в горизонтальном направлении. Чтобы записать периодический процесс, точка должна за некоторый конечный промежуток времени переместиться слева направо по экрану и в возможно короткий промежуток времени вернуться обратно. Поэтому напряжение, подаваемое на горизонтально отклоняющие пластины, должно иметь пилообразный вид (см., например, рис. 18.8, причем T₁ >> Т₂). Принцип устройства, служащего для этой цели, — генератора развертки — был рассмотрен в § 18.5.

Для того чтобы периодический процесс отображался на экране неподвижным изображением, необходимо подобрать достаточно точно частоту развертки: на один период времени развертки должно приходиться целое число периодов исследуемого сигнала. Это условие выполняется блоком синхронизации развертки. Ручки «Диапазон частот» и «Частота плавно» позволяют задавать нужную частоту развертки.

Если исследуемый процесс однократный или непериодический, то может быть использован ждущий режим развертки, предусмотренный в некоторых осциллографах. Этот режим развертки действует каждый раз и только тогда, когда возникает регистрируемый процесс.

Вращая ручки «Яркость» и «Фокус», изменяют разность потенциалов между ускоряющими электродами, благодаря чему достигаются различная интенсивность и площадь сечения электронного пучка. При этом происходит изменение яркости и фокусировки светящейся точки. Ручки «Ось У» и «Ось X» служат для смещения всей изображаемой картины в вертикальном или горизонтальном направлении.

Для наблюдения зависимости каких-либо двух величин подают электрические сигналы, отвечающие этим величинам, на клеммы «Вход У» и «Вход X». Генератор развертки при этом не включается. Так, в частности, можно получить фигуры Лиссажу (см. § 5.3) вектор-кардиограмму (см. § 12.5).

С помощью ручки «Усиление» изменяют усиление поданного сигнала. При этом на экране осциллографа изображение растягивается или сжимается по соответствующему направлению.

Для калибровки масштаба времени в некоторых осциллографах предусмотрен генератор меток времени для периодического изменения яркости пятна на экране. Благодаря этому можно определять длительность изображаемого процесса или его отдельных частей.

Изображение, полученное на экране электронного осциллографа, может быть сфотографировано.

РАЗДЕЛ 6

Оптика

Оптика— раздел физики, в котором рассматриваются закономерности излучения, поглощения и распространения света. В физике термин «свет» применяют не только к излучению, воспринимаемому глазом человека, но и к невидимому излучению. Природа света двойственна, дуалистична. Это означает, что свет проявляет себя и как электромагнитная волна, и как поток частиц — фотонов. Дуализм света, в частности, отражается формулой е = hv, так как энергия е фотона является квантовой характеристикой, а частота колебаний v — характеристикой волнового процесса.

В одних оптических явлениях в большей степени проявляются волновые свойства света, а в других — корпускулярные. Двойственная природа присуща также и частицам — электрону, протону и т. д.

Так как свет обладает электромагнитной природой, то оптику целесообразно изучать после электродинамики. Вопросы излучения света граничат с атомной физикой и существенно с ней связаны. Поэтому раздел «Оптика» предшествует атомной физике.

В развитии физики оптические наблюдения, эксперименты и теории сыграли особую роль: прямолинейное распространение света и его отражение от зеркальных поверхностей было известно еще задолго до нашей эры; интерференционный опыт Майкельсона явился экспериментальным основанием теории относительности; гипотеза Планка о дискретности излучения положила начало квантовой физике.

Исследования видимого света и связанные с этим измерения относятся не только к области физики, но и к физиологии. В этом отношении оптика подобна акустике.

Для медиков и биологов эти знания прежде всего важны при исследовании биологических объектов: микроскопия, спектрометрия, рефрактометрия, поляриметрия, колориметрия. Кроме того, врачам следует знать физические основы использования теплового излучения для диагностики заболевания (термография), устройство аппаратуры светолечения и другие вопросы.

Глава 19

Интерференция и дифракция света. Голография

Под интерференцией света понимают такое сложение световых волн, в результате которого образуется устойчивая картина их усиления и ослабления. Для получения интерференции света необходимо выполнение определенных условий. Дифракцией света называют явление отклонения света от прямолинейного распространения в среде с резкими неоднородностями. Возможность наблюдения дифракции зависит, в частности, от соотношения длины волны и размеров неоднородностей. Различают с некоторой степенью условности дифракцию сферических волн (дифракция Френеля) и дифракцию плоскопараллельных волн (дифракция Фраунгофера). Описание дифракционной картины возможно с учетом интерференции вторичных волн. В главе рассматривается голография как метод, основанный на интерференции и дифракции.

§ 19.1. Когерентные источники света. Условия для наибольшего усиления и ослабления волн

Сложение волн, распространяющихся в среде, определяется сложением в разных точках пространства соответствующих колебаний. Наиболее простой случай сложения электромагнитных волн наблюдается тогда, когда их частоты одинаковы и направления электрических векторов совпадают. В этом случае амплитуду результирующей волны можно найти по формуле (5.30), которую для амплитуды напряженности электрического поля запишем в виде

где Dj — разность фаз слагаемых волн (колебаний).

В зависимости от типа источников света результат сложения волн может быть принципиально различным.

Сначала рассмотрим сложение волн, идущих от обычных источников света (лампа, пламя, Солнце и т. п.). Каждый такой источник представляет совокупность огромного количества излучающих атомов. Отдельный атом излучает электромагнитную волну приблизительно в течение 10~⁸ с, причем излучение есть событие случайное, поэтому и разность фаз Dj в формуле (19.1) принимает случайные значения. При этом среднее по излучениям всех атомов значение cosDj равно нулю. Вместо (19.1) получаем усредненное равенство для тех точек пространства, где складываются две волны, идущие от двух обычных источников света:

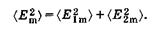(19.2)

Так как интенсивность волны пропорциональна квадрату амплитуды [см. (14.60)], то из (19.2) имеем условие сложения интенсивностей I1 и I₂ волн:

(19.3)

Это означает, что для интенсивностей излучений, исходящих от двух (или более) обычных световых источников, выполняется достаточно простое правило сложения: интенсивность суммарного излучения равна сумме интенсивностей слагаемых волн. Это наблюдается в повседневной практике: освещенность от двух ламп равна сумме освещенностей, создаваемых каждой лампой в отдельности.

Если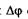остается неизменной во времени, наблюдается интерференция света. Интенсивность результирующей волны принимает в разных точках пространства значения от минимального до некоторого максимального.

Интерференция света возникает от согласованных, когерентных источников, которые обеспечивают постоянную во времени разность фаз Dj у слагаемых волн в различных точках. Волны, отвечающие этому условию, называют когерентными.

Интерференция могла бы быть осуществлена от двух синусоидальных волн одинаковой частоты, однако на практике создать такие световые волны невозможно, поэтому когерентные волны получают, «расщепляя» световую волну, идущую от источника.

Такой способ применяется в методе Юнга. На пути сферической волны, идущей от источника S, устанавливается непрозрачная преграда с двумя щелями (рис. 19.1). Точки волновой поверхности, дошедшей до преграды, становятся центрами когерентных вторичных волн,

22* поэтому щели можно рассматривать как когерентные источники. На экране Э наблюдается интерференция.

Другой метод заключается в получении мнимого изображения S' источника S (рис. 19.2) с помощью зеркала (зеркало Ллойда). Источники S и S' являются когерентными. Они создают условия для интерференции волн. На рисунке показаны два интерферирующих луча, попадающие в некоторую точку А экрана Э.

Так как время т излучения отдельного атома ограничено, то разность хода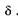лучей 1 и 2 при интерференции не должна быть слишком большой, в противном случае в точке А встретятся некогерентные волны. Наибольшее значение 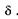для интерференции определяется через скорость света и время излучения атома:

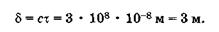(19.4)

Реальные источники состоят из множества беспорядочно излучающих атомов, поэтому время t' их согласованного излучения на много порядков меньше времени излучения т отдельного атома. Вследствие этого реальная разность хода d' интерферирующих лучей должна быть на много порядков меньше, чем величина 5, определяемая формулой (19.4).

Расчет интерференционной картины можно сделать, используя формулу (19.1), если известны разность фаз интерферирующих волн и их амплитуды. Практический интерес представляют частные случаи: наибольшее усиление волн — максимум интенсивности (max), наибольшее ослабление — минимум интенсивности (min).

Отметим, что условия максимумов и минимумов интенсивностей удобнее выражать не через разность фаз, а через разность хода волн, так как пути, проходимые когерентными волнами при интерференции, обычно известны. Покажем это на примере интерференции плоских волн / и //, векторы Е которых перпендикулярны плоскости чертежа (рис. 19.3).

Колебания векторов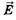этих волн в некоторой точке В, удаленной на расстояния x1 и х2соответственно от каждого источника, происходят по гармоническому закону

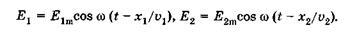(19.5)

Для общности вывода предположим, что волны распространяются в разных средах¹ с показателями преломленияиСкорости распространения волн соответственно равны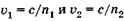, где с — скорость света в вакууме. Тогда из (19.5) следует выражение для разности фаз

Так как длина волны в вакуумето вместо (19.6) имеем

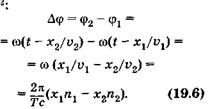
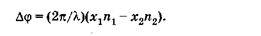(19.7)

Произведение геометрического пути волны на показатель преломления среды, т. е. хп, называют оптической длиной пути, а разность этих путей

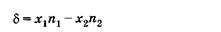(19.8)

— оптической разностью хода волн.

На основании (19.7) и (19.8) получим связь между разностью фаз и оптической разностью хода интерферирующих волн:

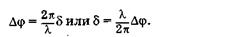(19.9)

Используя законы сложения колебаний (см. § 5.3.) и соотношение (19.9), получаем условия максимума и минимума интенсивности света при интерференции — соответственно

Следовательно, максимум при интерференции наблюдается в тех точках, для которых оптическая разность хода равна целому числу длин волн (четному числу полуволн), минимум — в тех точках, для которых оптическая разность хода равна нечетному числу полуволн.

^{____________________________}

¹Схематичность рис. 19.3 не позволяет показать разные среды распространения для различных волн.

²Полезно заметить, что так как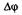не зависит от времени, то слагаемые волны являются когерентными.

19.2. Интерференция света в тонких пластинках (пленках). Просветление оптики

Образование когерентных волн и интерференция происходят также при попадании света на тонкую прозрачную пластинку или пленку.

Пучок света падает на плоскопараллельную пластинку (рис. 19.4). Луч 1 из этого пучка попадает в точку А, частично отражается (луч 2), частично преломляется (луч AM). Преломленный луч испытывает отражение на нижней границе пластинки в точке М. Отраженный луч, преломившись в точке В, выходит в первую среду (луч 3). Лучи 2 и 3 образованы от одного луча, поэтому они когерентны и будут интерферировать.

Найдем оптическую разность хода лучей 2 и 3. Для этого из точки В проведем нормаль ВС к лучам. От прямой ВС до встречи лучей их оптическая разность хода не изменится, линза или глаз не внесут дополнительной разности фаз. До расхождения в точке А эти лучи в совокупности с другими, параллельными им, не показанными на рис. 19.4, формировали луч 1 и поэтому, естественно, имели одинаковую фазу. Луч 3 прошел расстояние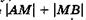в пластинке с показателем преломления п, луч 2 — расстояниев воздухе, поэтому их оптическая разность хода

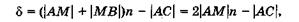(19.12)

так как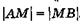. Согласно закону преломления,

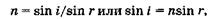(19.13)

где i — угол падения, г — угол преломления.

Из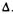АМО находим: 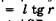(/ — толщина пластинки). Из 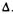АСВнаходим

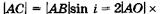
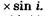
Учитывая эти равенства, а также (19.13), получаем

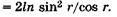
Тогда оптическая разность хода интерферирующих волн равна

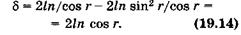
Рис.19.4

В формуле (19.14) не учтено одно важное обстоятельство. Опыт показывает, что при отражении света от среды оптически более плотной, т. е. с большим показателем преломления, фаза волны изменяется на п, что соответствует [см. (19.9)] изменению оптической разности хода на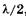, т. е. при отражении света от среды оптически более плотной происходит «потеря полволны»¹.

Если бы оба луча 2 vs. 3 теряли пол волны, то это не изменило бы выражения для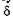(19.14). Однако луч 2 отражается от среды оптически более плотной (точка А) и теряет полволны, а луч 3 отражается от среды оптически менее плотной (точка М), его фаза при этом не изменяется. С учетом потери полволны оптическая разность хода

(19.15)

Так как, то d можно выразить и через угол падения:

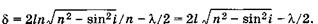(19.16)

Для максимума интерференции [см. (19.10), (19.16)] имеем

(19.17)

Для минимума интерференции [см. (19.11), (19.16)] имеем²

(19.18)

Формулы (19.17) и (19.18) соответствуют интерференции в отраженном свете. Интерференция в проходящем через пластинку свете показана на рис. 19.5; изображены только те лучи, которые необходимы для понимания явления. Читатель может самостоятельно вывести соответствующие фор-
мулы и убедиться, что для этого случая (19.17) соответствует минимуму интерференции, а (19.18) —
максимуму. С учетом закона сохранения энергии это понятно, так как интерференция есть перерас- пределение световой энергии: падающий поток перераспределяется пластинкой на отраженный и

Рис. 19.5

проходящий (поглощением здесь пренебрегаем), причем если отраженный максимален, то проходящий минимален, и наоборот.

Интерференция при отражении наблюдается более отчетливо, чем в проходящем свете, что обусловлено существенным различием интенсивностей отраженного и проходящего лучей. Если принять, что на границе раздела прозрачных сред отражается около 5% падающей энергии, то

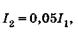(19.19)

где— интенсивности лучей 1 м 2 соответственно (см. рис.19.4). Интенсивность луча 3 с учетом двукратного преломления и однократного отражения равна

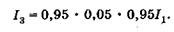(19.20)

Из (19.19) и (19.20) имеем

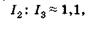(19.21)

что означает приближенное равенство амплитуд интерферирующих лучей при отражении: условие минимума соответствует почти полной темноте. Делая аналогичный расчет для проходящего света (рис. 19.5), получаем

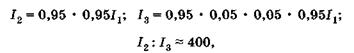
или для амплитуд

(19.22)

Из (19.22) видно, что в проходящем свете интерферируют волны с существенно различными амплитудами, поэтому максимумы и минимумы мало отличаются друг от друга и интерференция слабо заметна.

Проанализируем зависимости (19.17) и (19.18).

Если на тонкую плоскопараллельную пластинку под некоторым углом падает параллельный пучок монохроматического излучения, то, согласно этим формулам, пластинка в отраженном свете выглядит яркой или темной.

При освещении пластинки белым светом условия максимума и минимума выполняются для отдельных длин волн, пластинка станет окрашенной, причем цвета в отраженном и проходящем свете будут дополнять друг друга до белого.

При падении монохроматического света на пластинку переменной толщины каждому значению I соответствует
свое условие интерференции, поэтому пластинка пересечена светлыми и тем ными линиями (полосами) — линиями равной толщины. Так, в клине это система параллельных линий (рис. 19.6), в воздушном промежутке между линзой и пластинкой — кольца (кольца Ньютона).

Рис. 19.6

При освещении пластинки переменной толщины белым светом получаются разноцветные пятна и линии: окрашенные мыльные пленки, пленки нефти и масла на поверхности воды, переливчатые цвета крыльев некоторых насекомых и птиц. В этих случаях не обязательна полная прозрачность пленок.

Особый практический интерес имеет интерференция в тонких пленках в связи с созданием устройств, уменьшающих долю световой энергии, отраженной оптическими системами, и увеличивающих, следовательно, энергию, поступающую к регистрирующим системам — фотопластинке, глазу и т. п. С этой целью поверхности оптических систем покрывают тонким слоем оксидов металлов так, чтобы для некоторой средней для данной области спектра длины волны был минимум интерференции в отраженном свете. В результате возрастает доля прошедшего света. Покрытие оптических поверхностей специальными пленками называют просветлением оптики, а сами оптические изделия с такими покрытиями — просветленной оптикой.

Если на стеклянную поверхность нанести ряд специально подобранных слоев, то можно создать отражательный светофильтр, который вследствие интерференции будет пропускать или отражать излучение в определенном интервале длин волн.

¹Для циклических процессов не имеет значения, уменьшается или увеличивается фаза на к, поэтому равноценно было бы говорить не о потере, а о приобретении полволны, однако такая терминология не употребляется.

²Для того чтобы при максимумах и минимумах сохранить для k те же значения (0, 1, 2 и т. д.), формулу (19.16) для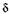записываем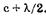

§ 19.3. Интерферометры и их применение. Понятие об интерференционном микроскопе

Интерференцию света используют в специальных приборах — интерферометрах — для измерения с высокой степенью точности длин волн, небольших расстояний, показателей преломления веществ и определения качества оптических поверхностей.

На рис. 19.7 изображена принципиальная схема интерферометра Майкельсона, который относится к группе двухлучевых, так как световая волна в нем раздваивается¹ и обе ее части, пройдя разный путь, интерферируют.

Луч 1 монохроматического света от источника S падает под углом 45° на плоскопараллельную стеклянную пластинку А, задняя поверхность которой полупрозрачна, так как покрыта очень тонким слоем серебра. В точке О этот луч расщепляется на два луча 2 и 3, интенсивность которых приблизительно одинакова.

Луч 2 доходит до зеркала /, отражается, преломляется в пластине А и частично выходит из пластины — луч 2'. Луч 3 из точки О идет к зеркалу //, отражается, возвращается к пластине А, где частично отражается, — луч 3'. Лучи 2' и 3', попадающие в глаз наблюдателя, когерентны, их интерференция может быть зарегистрирована.

Обычно зеркала I и II располагают так, что лучи 2 и 3 от расхождения до встречи проходят пути одинаковой длины. Чтобы и оптическую длину путей сделать одинаковой, на пути луча 3 устанавливают прозрачную пластину В, аналогичную А, для компенсации двух путей, пройденных лучом 2 через пластину А. В этом случае наблюдается максимум интерференции.

Если одно из зеркал сдвинуть на расстояние, то разность хода лучей станет к/2, что соответствует минимуму, произойдет смещение интерференционной картины на 0,5 полосы². Если зеркало от первоначального положения переместить на расстояние к/2, то оптическая разность хода
интерферирующих лучей изменится на к, что соответствует максимуму, произойдет смещение интерференционной картины на целую полосу. Такая связь между перемещением зеркала и изменением интерференционной картины позволяет измерять длину волны по перемещению зеркала и, наоборот, перемещение по длине волны.

Интерферометр Майкельсона применяют для измерения показателя преломления. На пути лучей 2 и 3 устанавливают одинаковые кюветы К (показаны штриховыми линиями на рис. 19.7), одна из которых наполнена веществом с показателем преломления n1 а другая — с п₂. Оптическая разность хода лучей

Рис. 19.7

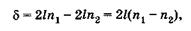(19.23)

где I — длина однократного пути луча в среде, заполняющей кюветы; так как лучи проходят кювету дважды, то расстояние равно 21. Предположим, что вследствие этой разности хода интерференционная картина смещается на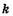полос, тогда

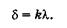(19.24)

Приравнивая (19.23) и (19.24), получаем

(19.25)

Если считать, что смещение на 0,1 полосы (к = 0,1) может быть зафиксировано, то, например, приимеем

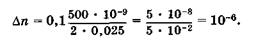
Как видно, интерференционный рефрактометр (интерферометр, приспособленный для измерения показателя преломления) способен фиксировать изменения показателя преломления в шестом знаке после запятой.

Интерференционный рефрактометр применяют, в частности, с санитарно-гигиеническими целями для определения содержания вредных газов.

С использованием интерферометра Майкельсон доказал независимость скорости света от движения Земли, что явилось одним из опытных фактов, способствовавших созданию специальной теории относительности.

Сочетание двухлучевого интерферометра и микроскопа, получившее название интерференционного микроскопа, используют в биологии для измерения показателя преломления, концентрации сухого вещества и толщины прозрачных микрообъектов.

Принципиальная схема интерференционного микроскопа пока
зана на рис. 19.8. Луч света, как и в интерферометре, в точке А раздваивается,один луч проходит через прозрачный микрообъект М, а другой — вне его. В точке Д лучи соединяются и интерферируют, по результату интерференции судят об измеряемом параметре.

Рис. 19.8

1 1 Строго говоря, вследствие многократных отражений может образоваться более чем два луча, однако их интенсивности незначительны

2 2 Вследствие разных углов падения лучей из S на пластину А или не строгой перпендикулярности зеркал I и II интерференционная картина практически всегда представлена полосами (полосы равного наклона или равной толщины соответственно). Этот вопрос подробно не рассматривается.

§ 19.4. Принцип Гюйгенса—Френеля

Объяснение и приближенный расчет дифракции света можно осуществить, используя принцип Гюйгенса—Френеля.

Согласно Гюйгенсу, каждая точка волновой поверхности, которой достигла в данный момент волна, является центром элементарных вторичных волн, их внешняя огибающая будет волновой поверхностью в последующий момент времени (рис. 19.9; S_l и S₂ — волновые поверхности соответственно в моменты t_t и t₂; t₂ > tj).

Френель дополнил это положение Гюйгенса, введя представление о когерентности вторичных волн и их интерференции. В таком обобщенном виде эти идеи получили название принципа Гюйгенса—Френеля.

Для того чтобы определить результат дифракции в некоторой
точке пространства, следует рассчитать, согласно принципу Гюй
генса—Френеля, интерференцию вторичных волн, попавших в эту
точку от различных элементов волновой поверхности. Для волновой поверхности произвольной формы такой расчет достаточно сложен, но в отдельных случаях (сферическая или плоская волновая поверхность, симметричное расположение точки относительно волновой поверхности и непрозрачной преграды) вычисления сравнительно

Рис. 19.9

просты. Волновую поверхность при этом разбивают на отдельные участки (зоны Френеля), расположенные определенным образом, что упрощает математические операции.

§ 19.5. Дифракция на щели в параллельных лучах

На узкую длинную щель, расположенную в плоской непрозрачной преграде MN, нормально падает плоскопараллельный пучок монохроматического света (рис. 19.10; АВ = а — ширина щели; L — собирающая линза, в фокальной плоскости которой рас- -положен экран Э для наблюдения дифракционной картины).

Если бы не было дифракции, то световые лучи, пройдя через щель, сфокусировались бы в точке О, лежащей на главной оптической оси линзы. Дифракция света на щели существенно изменяет явление.

Рис. 19.10

Будем считать, что все лучи пучка света исходят от одного удаленного источника¹ и, следовательно, когерентны. АВ есть часть волновой поверхности, каждая точка которой является центром вторичных волн, распространяющихся за щелью по всевозможным направлениям. Изобразить все эти вторичные волны невозможно, поэтому на рис. 19.10 показаны только вторичные волны, распространяющиеся под углом а к направлению падающего пучка и нормали к решетке. Линза соберет эти волны в точке О' экрана, где и будет наблюдаться их интерференция. (Положение точки О' получают как пересечение с фокальной плоскостью побочной оси СО' линзы, проведенной под углом а.)

Чтобы узнать результат интерференции вторичных волн, проделаем следующие построения. Проведем перпендикуляр AD к направлению пучка вторичных волн. Оптические пути всех вторичных волн от AD до О' будут одинаковыми, поскольку линза не вносит добавочной разности фаз между ними, поэтому та разность хода, которая образовалась у вторичных волн к AD, будет сохранена и в точке О'.

Разобьем BD на отрезки, равные l/2. В случае, показанном на рис. 19.10, получено три таких отрезка: \ВВ₂\ = \В₂В_г\ = \B₁D\ = = l/2. Проведя из точек В₂ и В1 прямые, параллельные AD, разделим АВ на равные зоны Френеля: \АА_г\ = \А1А₂\ = \А₂В\. Любой вторичной волне, идущей от какой-либо точки одной зоны Френеля, можно найти в соседних зонах соответствующие вторичные волны такие, что разность хода между ними будет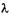/2. Например, вторичная волна, идущая от точки А₂ в выбранном направлении, проходит до точки О' расстояние на/2 больше, чем волна, идущая от точки A1, и т. д. Следовательно, вторичные волны, идущие от двух соседних зон Френеля, погасят друг друга, так как различаются по фазе на.

Число зон, укладывающихся в щели, зависит от длины волны 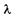и угла 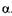. Если щель АВ можно разбить при построении на нечетное число зон Френеля, a BD — на нечетное число отрезков, равных 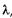/2, то в точке О' наблюдается максимум интенсивности света:

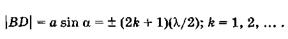(19.26)

Направление, соответствующее углу а = 0, также отвечает максимуму, так как все вторичные волны придут в О в одинаковой фазе.

Если щель АВ можно разбить на четное число зон Френеля, то наблюдается минимум интенсивности света:

(19.27)

Таким образом, на экране Э получится система светлых (максимум) и темных (минимум) полос, центрам которых соответствуют условия (19.26) и (19.27), симметрично расположенных влево и вправо от центральной (а = 0), наиболее яркой, полосы. Интенсивность I остальных максимумов быстро убывает по мере удаления от центрального максимума (рис. 19.11).

Если щель освещать белым светом, то на экране Э [см. (19.26), (19.27)] образуется система цветных полос, лишь центральный максимум будет сохранять цвет падающего света, так как при а = 0 усиливается свет всех длин волн.

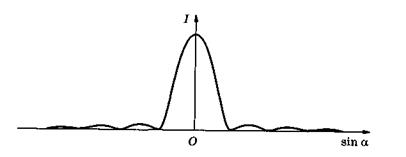
Рис. 19.11

Дифракция света, как и интерференция, связана с перераспределением энергии электромагнитных волн в пространстве. В этом смысле щель в непрозрачном экране является не просто системой, ограничивающей поступление светового потока, но перераспределителем этого потока в пространстве.

Чтобы понять влияние соотношения между шириной щели и длиной волны на возможность наблюдения дифракционной картины, рассмотрим некоторые частные случаи:

1)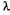<< а. Представив формулу для максимумов в виде

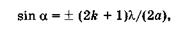
имеем sin a ~ 0 практически для всех максимумов, и дифракция при этом не наблюдается. Этот случай соответствует достаточно широкой, по сравнению с длиной волны, щели. Так, например, не удается осуществить дифракцию в комнате при прохождении света через окно;

2)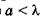. На основании (19.27) для первых минимумов, которые ограничивают центральную светлую полосу, можно записать

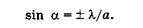
Отсюда следует, что при заданном условии sin а формально превышает единицу, чего не может быть. Практически в этом случае вместо системы максимумов и минимумов весь экран будет слабо освещен.

¹ Практически точечный источник можно расположить в фокусе линзы, не показанной на рис. 19.10, так, что от линзы будет распространяться параллельный пучок когерентных волн.

§ 19.6. Дифракционная решетка. Дифракционный спектр

Дифракционная решетка — оптическое устройство, представляющее собой совокупность большого числа параллельных, обычно равноотстоящих друг от друга, щелей.

Дифракционную решетку можно получить нанесением непрозрачных царапин (штрихов) на стеклянную пластину. Непроцарапанные места — щели — будут пропускать свет; штрихи, соответствующие промежутку между щелями, рассеивают и не пропускают света. Сечение такой дифракционной решетки (о) и ее условное обозначение (б) показанына рис. 19.12. Суммарную ширину щели а и промежутка Ъ между щелями называют постоянной или периодом дифракционной решетки:

Рис. 19.12 (19.28)

Если на решетку падает пучок когере

<79 80 818283 84 85 >

Дата добавления: 2020-11-18; просмотров: 323;