Оценка параметров генеральной совокупности по ее выборке
Предположим, что генеральная совокупность является нормальным распределением (здесь вместо вероятности следует использовать относительную частоту). Нормальное распределение полностью определено математическим ожиданием (средним значением) и средним квадратическим отклонением. Поэтому если по выборке можно оценить, т. е. приближенно найти, эти параметры, то будет решена одна из задач математической статистики — определение параметров большого массива по исследованию его части.
Как и для выборки, для генеральной совокупности можно определить генеральную среднюю хr — среднее арифметическое значение всех величин, составляющих эту совокупность. Учитывая большой объем этой совокупности, можно полагать, что генеральная средняя равна математическому ожиданию:
где X — общая запись случайной величины (значения изучаемого признака) генеральной совокупности.
Рассеяние значений изучаемого признака генеральной совокупности от их генеральной средней оценивают генеральной дисперсией
(N — объем генеральной совокупности) или генеральным средним квадратическим отклонением
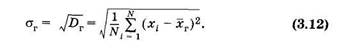
Точечная оценка.Предположим, что из генеральной совокупности производятся разные выборки; делают это так, чтобы вся генеральная совокупность сохранялась неизменной. Для определенности будем считать объемы этих выборок одинаковыми и равными п. Их выборочные средние х1, х2, ..., xi., ... являются случайными величинами, которые распределены по нормальному закону (см. конец § 2.3), а их математическое ожидание равно математическому ожиданию генеральной совокупности, т. е.генеральной средней:
На практике иногда при достаточно большой выборке за генеральную среднюю приближенно принимают выборочную среднюю. Для дисперсий положение получается несколько иным. Математическое ожидание дисперсий различных выборок [M(Dвi)], составленных из генеральной совокупности, отличается от генеральной дисперсии:
Прибольшом п получаем
Длягенерального среднего квадратического отклонения соответственно из (3.14) и (3.14а) получаем:
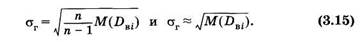
На практике иногда при достаточно большой выборке выборочное среднее квадратическое отклонение приближенно принимают за генеральное среднее квадратическое отклонение. Так, если считать, что статистическое распределение (см. табл. 5) является выборкой из некоторой генеральной совокупности, то на основании (3.6) и (3.9) можно заключить, что для этой генеральной совокупности xr ≈ 3,468 кг и σг ≈ 0,3896 кг.
Такого рода оценка параметров генеральной совокупности или каких-либо измерений определенными числами называется точечной оценкой.
Интервальная оценка генеральной средней.Точечная оценка, особенно при малой выборке, может значительно отличаться от истинных параметров генеральной совокупности. Поэтому при небольшом объеме выборки пользуются интервальными оценками.
В этом случае указывается интервал (доверительный интервал, или доверительные границы), в котором с определенной (доверительной) вероятностью р находится генеральная средняя.
Иначе говоря, р определяет вероятность, с которой осуществляются следующие неравенства: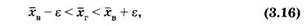 
зуя функцию (3.18). Пределы интегрирования необходимо взять из выражения (3.19):
где положительное число е характеризует точность оценки.
Кроме доверительной вероятности используют «противоположное» понятие — уровень значимости
который выражает вероятность непопадания генеральной средней в доверительный интервал.
Доверительную вероятность не следует выбирать слишком маленькой (не следует ее обесценивать). Наиболее часто р принимают равной 0,95; 0,99; 0,999. Чем больше р, тем шире интервал, т. е. тем больше е. Чтобы установить количественную связь между этими величинами, необходимо найти выражение для доверительной вероятности. Это можно сделать, используя (2.17), однако нужно понять, что при этом следует взять за функцию распределения вероятностей и какие принять пределы интегрирования. Рассмотрим этот вопрос.
Итак, генеральная совокупность распределена по нормальному закону с математическим ожиданием (средним значением) хГ и дисперсией DT. Если из этой генеральной совокупности брать разные выборки с одинаковым объемом п, то можно для каждой выборки получить среднее значение хв. Эти средние значения сами являются случайными величинами. Их распределение, т. е. распределение средних значений разных выборок, полученных из одной генеральной совокупности, будет нормальным со средним значением, равным среднему значению генеральной совокупности хт, дисперсией — и средним квадратическим отклонением (см. конец § 2.2).
Таким образом, хв уже выступает как случайная величина, для нее можно записать следующую функцию распределения вероятностей [см. (2.22)]:
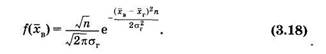
Из (3.16) можно записать для хв следующие неравенства:
Вероятность того, что хв попадает в этот интервал (доверительную вероятность), можно найти по общей формуле нахождения р по х или т по р можно воспользоваться таол. ( или таблицей функции Ф (см. [2]).
Результаты интегрирования (3.20) найдем, используя функцию Ф (см. § 2.3). По формуле (2.25) получим
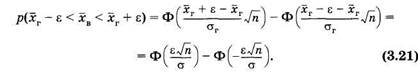
Обозначая
и учитывая (см. § 2.3), что Ф(-τ) = 1 - Ф(τ), получим из (3.21):
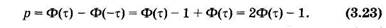
Таблица 7
| τ | ||||||||||
| 0,0 | 0,5 | 0,5040 | 0,5080 | 0,5120 | 0,5160 | 0,5199 | 0,5239 | 0,5279 | 0,5319 | 0,5359 |
| 0,4 | ||||||||||
| 0,9 | ||||||||||
| 1,4 | ||||||||||
| 1,9 |
Хотя неравенства (3.16) и (3.19) по существу идентичны, но для практических целей важнее запись (3.16), так как она позволяет решить главную задачу — при заданной доверительной вероятности и найденной выборочной средней найти доверительный интервал, в который попадает генеральная средняя.
Запишем неравенство (3.16), подставив в него выражение εиз формулы (3.22):
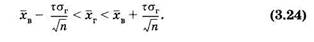
Практически при нахождении доверительного интервала по формуле (3.24) берут выборочную среднюю некоторой конкретной выборки (объем п > 30), а вместо генеральной средней квадратичной используют выборочную среднюю квадратичную этой же выборки. Поясним это некоторым примером. Вновь обратимся к данным таблиц, считая их выборкой. Найдем доверительный интервал для генеральной средней, из которой эта выборка получена, считая доверительную вероятность равной р = 0,95. Из (3.23) для такой доверительной вероятности получаем: Ф(τ) = 0,975.
В табл. 7 левый вертикальный столбец содержит значения с точностью до десятых долей, а верхняя горизонтальная строчка дает сотые доли т, поэтому для Ф(х) = 0,975 имеем х = 1,9 + 0,06= = 1,96. Подставляя это значение τ, выборочную среднюю (3.6), выборочное среднее квадратическое отклонение (3.9) и объем выборки (п = 100) в выражение (3.24),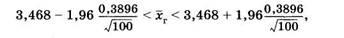 
или
Интервальная оценка генеральной средней при малой выборке.При достаточно большом объеме выборки можно сделать вполне надежные заключения о генеральной средней. Однако на практике часто имеют дело с выборками небольшого объема (п < 30). В этом случае в выражении доверительного интервала (3.16) точность оценки определяется по следующей формуле:
где t — параметр, называемый коэффициентом Стьюдента (его находят из распределения Стьюдента; оно здесь не рассматривается), который зависит не только от доверительной вероятности р, но и от объема выборки п. Коэффициент Стьюдента. Запишем неравенство (3.16), подставив в него выражение из формулы (3.26): 4п - 1
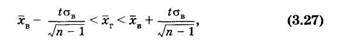
Поясним использование формулы (3.26) следующим примером. Предположим, что из генеральной совокупности, которую использовали при составлении выборки (см. табл. 5), взяли 10 случайных данных и получили следующее распределение (табл. 9):
Таблица 9
| Масса, кг | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,7 | 3,8 | 4,0 | 4,4 |
| Частота |
Отсюда можно вычислить хв = 3,54 кг, DB = 0,19156 кг2 и св = 0,43767 кг. Задав доверительную вероятностью = 0,95, находим для объема выборки п — 10 параметр t = 2,26. Подставляя эти данные в (3.26), получаем для доверительного интервала [см. (3.27)]:
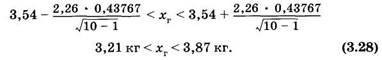
Полезно сопоставить соотношения, полученные для большой (3.25) и малой (3.28) выборок.
Интервальная оценка истинного значения измеряемой величины.Интервальная оценка генеральной средней может быть использована для оценки истинного значения измеряемой величины.
Пусть несколько раз измеряют одну и ту же физическую величину. При этом по разным случайным причинам, вообще говоря, получают разные значения: x1 x2, х3, ... . Будем считать, что нет преобладающего влияния какого-либо фактора на эти измерения.
Истинное значение измеряемой величины (xист) совершенно точно измерить невозможно хотя бы по причине несовершенства измерительных приборов. Однако можно дать интервальную оценку для этого значения.
Если значения x1 x2, х3, ... рассматривать как варианты выборки, а истинное значение измеряемой величины хист как аналог генеральной средней, то можно по описанным выше правилам найти доверительный интервал, в который с доверительной вероятностью р попадает истинное значение измеряемой величины. Применительно к малому числу измерений (п < 30) из (3.27) получим:
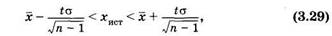
где х — среднее арифметическое значение из полученных измерений, а σ — соответствующее им среднее квадратическое отклонение, t — коэффициент Стьюдента.
Более подробно и разносторонне оценка результатов измерений рассматривается в практикуме (см. [1]).
Проверка гипотез
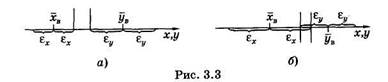
В медико-биологических исследованиях актуальной является задача сравнения выборок, полученных в результате эксперимента, заключающегося в том или ином воздействии на объект. Фактически конечный результат исследования зависит от достоверности различий значений случайной величины в контроле (до воздействия или без него) и опыте (после воздействия). Наиболее просто решается задача определения достоверности различий статистических распределений, если предварительно для выборок рассчитаны доверительные интервалы. Положим, есть два статистических распределения некоторых случайных величин X и У. Пусть генеральные средние этих распределений с доверительной вероятностью р = 0,95 находятся в доверительных интервалах (хв ± ех) и (ув ± s ), и пусть при этом ув > хв. Если соблюдается неравенство (г/в - ε ) > (хв + ε), то не вызывает сомнения, что случайная величина У существенно больше случайной величины X (см. рис. 3.3, а). Вероятность этого превышает 0,95.
На рис. 3.3, б представлен вариант, когда выборки частично пересекаются, т. е. когда выполняется неравенство (ув - еу) < (хв + гх). В этом случае целесообразно оценивать достоверность различий выборочных средних хв и ув с помощью дополнительных расчетов. Наиболее просто это сделать, предполагая, что случайные величины X и У распределены по нормальному закону. Условием существенности различия двух опытных распределений, являющихся выборками из различных генеральных совокупностей, является выполнение следующего неравенства для опытного и теоретического значений критерия Стьюдента: toa > teop. Для нахождения значения tов используют следующую формулу:
Здесь σх и σy — выборочные средние квадратические отклонения, пх и пу — число вариант в выборках (объемы выборок), хв и yв — выборочные средние значения.
Теоретическое значение tTeop находят по таблице 10, входными величинами которой являются доверительная вероятность р и параметр , связанный с числом вариант в выборках. Этот параметр определяют следующим образом. Если ах ≈σ , то f = пх + п - 2. Если же ах и а различаются на порядок и более, то величина определяется по формуле:
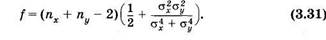
Используя этот способ оценки достоверности различия выборочных средних значений двух выборок, следует придерживаться такой последовательности действий. Во-первых, по экспериментальным данным нужно найти значения выборочных средних и средних квадратических отклонений для каждой выборки. Затем, сравнив величины σх и σy, найти величину f. После этого следует задать определенное значение доверительной вероятности и по таблице 10 найти tтеор. Затем по формуле (3.30) рассчитать ion.
Если при сравнении теоретического и опытного критериев Стьюдента окажется, что tou > tTeop, то различие между выборочными средними значениями случайных величин X и Y можно считать существенным с заданной доверительной вероятностью. В противоположном случае различия несущественны.
Представленный выше способ оценки достоверности различий выборок по выборочным средним является довольно простым. Существует большое число тестов и критериев для сравнения выборок и составления заключения о достоверности их различий. Как правило, при этом рассматривают вероятность двух взаимоисключающих гипотез. Одна из них, условно называемая «нулевой» гипотезой, заключается в том, что наблюдаемые различия между выборками случайны (т. е. фактически различий нет). Альтернативная гипотеза означает, что наблюдаемые различия статистически достоверны. При этом для оценки обоснованности вывода о достоверности различий используют три основных доверительных уровня, при которых принимается или отвергается нулевая гипотеза. Первый уровень соответствует уровню значимости (30 < 0,05) для второго уровня ро < 0,01. Наконец, третий доверительный уровень имеет р0 < 0,001. При соблюдении соответствующего условия нулевая гипотеза считается отвергнутой. Чем выше доверительный уровень, тем более обоснованным он считается. Фактически значимость вывода соответствует вероятности р = 1 . В медицинских и биологических исследованиях считают достаточным уже первый уровень, хотя наиболее ответственные выводы предпочтительнее делать с большей точностью. Одной из методик, позволяющих судить о достоверности различий статистических распределений, является ранговый тест Уилкоксона. Под рангом (Ri) понимают номер, под которым стоят исходные данные в ранжированном ряду. Если в двух сравниваемых выборках данному номеру соответствуют одинаковые варианты, то рангом этих вариант является среднее арифметическое двух рангов — данного и следующего за ним (см. пример). Покажем, как используется этот тест на примере сравнения двух равных по объему выборок.
Измеряли массу 13 недоношенных новорожденных (в граммах) в двух районах А и Б большого промышленного центра, один из которых (Б) отличался крайне неблагоприятной экологической обстановкой. Получены два статистических распределения (А) и (Б):
А: 970 990 1080 1090 1110 1120 ИЗО 1170 1180 1180 1210 1230 1270
Б: 780 870 900 900 990 1000 1000 1020 1030 1050 1070 1070 1100
Следует решить вопрос о том, достоверны ли различия между этими статистическими распределениями.
Составим общий ранжированный ряд с указанием номеров соответствующих вариант (RA Б) — рангов (строки А и Б соответствуют выборкам):
Как видно, варианта 990 встречается в первой и второй выборках, поэтому для нее рангом является среднее арифметическое значение 6 и 7.
Далее в ряду остаются лишь варианты первой выборки, поэтому ряд не закончен. Нулевая гипотеза состоит в том, что различий между выборками нет (они случайны и потому несущественны). Ранговый тест учитывает общее размещение вариант и размеры выборок, но не требует знания типа распределения. Основной вывод о верности нулевой гипотезы делается на основании анализа минимальной суммы рангов (из двух сумм для сравниваемых выборок), т. е. критерием является величина Т = ЯБ (учитывая, что Rв < Z -RA). При этом пользуются специальными таблицами. В частности, если число вариант в выборках одинаково (п1 = п2).
Критические значения величины r (теста Уилкоксона) при п1 = п2 = п для разных значений уровня значимости/
В этой таблице указаны две входные величины: число вариант в выборках и значение третьего и второго уровней значимости (Ро = 0,05 и 0,01). В нашем случае Т = RB = 110,5, что меньше табличного значения для п = 13 и βо < 0,01. Следовательно, на втором уровне значимости (р > 0,99) можно отвергнуть нулевую гипотезу. Таким образом, различия выборок достоверны с вероятностью, превышающей 0,99.
Дата добавления: 2020-11-18; просмотров: 421;
Поиск по сайту
Узнать еще
- II. Оценка материально-производственных запасов
- V. Оценка состояния здоровья детей и подростков
- А. Наилучшая статистическая оценка
- Автоматизированная система контроля геометрических параметров рам тележек ЛИС-РТ-3
- Автоматизированная система контроля технологических параметров ЮВС
- АВТОМАТИЧЕСКАЯ ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ ТОВАРНО-ТРАНСПОРТНЫХ ПОТОКОВ
- Алгоритм определения параметров
- Анализ активов организации и оценка эффективности их использования.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
