ПОНЯТИЕ О ПЛАСТИЧЕСКОМ ШАРНИРЕ
Рассмотрим данный вопрос на примере балки, нагруженной в середине возрастающей силой 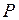 (рис. 3.8). Наибольший изгибающий момент получается в месте действия данной силы. Поэтому при возрастании силы
(рис. 3.8). Наибольший изгибающий момент получается в месте действия данной силы. Поэтому при возрастании силы 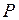 пластические деформации в первую очередь будут возникать в сечении, где приложена данная сила (сечение считается, к примеру, прямоугольным). Задача состоит в определении предельной силы
пластические деформации в первую очередь будут возникать в сечении, где приложена данная сила (сечение считается, к примеру, прямоугольным). Задача состоит в определении предельной силы 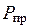 , при которой данное сечение прекращает сопротивляться дальнейшему росту нагрузки. Диаграмма
, при которой данное сечение прекращает сопротивляться дальнейшему росту нагрузки. Диаграмма 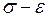 материала балки считается при этом идеальной упруго-пластической (рис. 3.1).
материала балки считается при этом идеальной упруго-пластической (рис. 3.1).
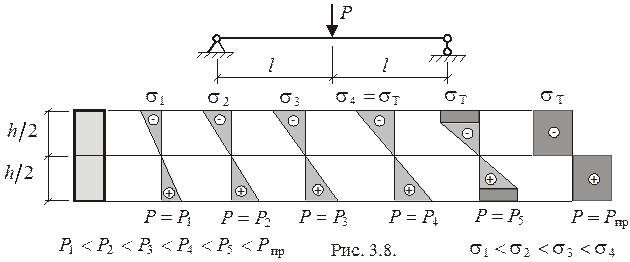
Проследим за изменением нормальных напряжений 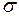 в сечении A-A при возрастании силы
в сечении A-A при возрастании силы 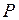 . Наибольшие напряжения возникают в крайних волокнах балки (рис. 3.8). По мере возрастания силы
. Наибольшие напряжения возникают в крайних волокнах балки (рис. 3.8). По мере возрастания силы 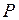 эти напряжения растут до значения
эти напряжения растут до значения 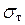 , после чего появляется область пластических деформаций, растущая внутрь сечения. Состояние, при котором эта область занимает все поперечное сечение балки, очевидно, является предельным. Разрушение происходит поворотом частей балки относительно друг друга. Такое состояние можно смоделировать введением так называемого пластического шарнира в среднем сечении балки, считая, что части балки, расположенные слева и справа от пластического шарнира, поворачиваются относительно друг друга как абсолютно твердые тела (рис. 3.9). При этом в сечениях непосредственно возле пластического шарнира действуют предельные внутренние моменты
, после чего появляется область пластических деформаций, растущая внутрь сечения. Состояние, при котором эта область занимает все поперечное сечение балки, очевидно, является предельным. Разрушение происходит поворотом частей балки относительно друг друга. Такое состояние можно смоделировать введением так называемого пластического шарнира в среднем сечении балки, считая, что части балки, расположенные слева и справа от пластического шарнира, поворачиваются относительно друг друга как абсолютно твердые тела (рис. 3.9). При этом в сечениях непосредственно возле пластического шарнира действуют предельные внутренние моменты 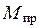 . В начале разрушения углы поворота частей балки можно считать величинами малыми. Тогда будет справедлив принцип возможных перемещений (принцип Лагранжа):
. В начале разрушения углы поворота частей балки можно считать величинами малыми. Тогда будет справедлив принцип возможных перемещений (принцип Лагранжа): 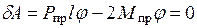 . Отсюда получаем
. Отсюда получаем 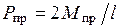 . Таким образом, для определения
. Таким образом, для определения 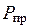 необходимо иметь предельный момент
необходимо иметь предельный момент 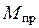 , создаваемый в сечении напряжениями
, создаваемый в сечении напряжениями 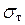 в состоянии предельного равновесия балки.
в состоянии предельного равновесия балки.

 Рассмотрим поперечное сечение, находящееся полностью в пластическом состоянии (рис. 3.10). Напряжения
Рассмотрим поперечное сечение, находящееся полностью в пластическом состоянии (рис. 3.10). Напряжения 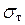 на элементарных площадках
на элементарных площадках 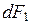 и
и 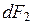 верхней (
верхней ( 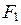 ) и нижней (
) и нижней ( 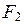 ) частей сечения создают в нем элементарный момент
) частей сечения создают в нем элементарный момент
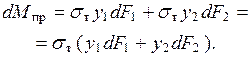
Тогда полный момент 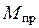 в сечении определяется интегрированием слагаемых в скобках по
в сечении определяется интегрированием слагаемых в скобках по 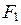 и
и 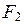 :
:
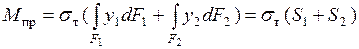 ,
,
где 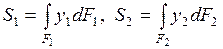 - статические моменты площадей
- статические моменты площадей 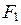 ,
, 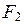 относительно оси
относительно оси 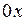 (нейтральной линии) сечения.
(нейтральной линии) сечения.
Полученное выражение для 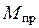 можно представить в виде, аналогичном упругому решению задачи:
можно представить в виде, аналогичном упругому решению задачи: 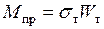 , где
, где 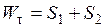 - пластический момент сопротивления изгибу. Так как сечение находится в предельном состоянии, то
- пластический момент сопротивления изгибу. Так как сечение находится в предельном состоянии, то 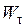 всегда меньше обычного момента сопротивления
всегда меньше обычного момента сопротивления 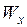 при упругом изгибе. В качестве примера найдем
при упругом изгибе. В качестве примера найдем 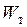 и
и 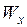 прямоугольного сечения (рис. 3.11).
прямоугольного сечения (рис. 3.11).

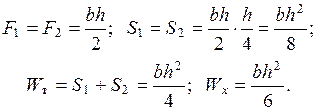
Это дает отношение 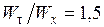 , означающее, что максимальная нагрузка для такого сечения в 1,5 выше той, которая будет при расчете по допускаемым напряжениям.
, означающее, что максимальная нагрузка для такого сечения в 1,5 выше той, которая будет при расчете по допускаемым напряжениям.
В заключении следует заметить, что положение нейтральной линии при пластическом изгибе в общем случае не совпадает с тем, которое имеет место при упругом изгибе. Это положение определяется из условия 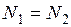 , где
, где 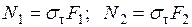 - равнодействующие напряжений
- равнодействующие напряжений 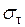 на частях
на частях 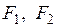 поперечного сечения, что в конечном итоге приводит к условию
поперечного сечения, что в конечном итоге приводит к условию 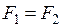 . При упругом изгибе положение нейтральной линии сечения, как известно из курса сопротивления материалов, находится из условия
. При упругом изгибе положение нейтральной линии сечения, как известно из курса сопротивления материалов, находится из условия 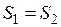 . В частном случае, когда
. В частном случае, когда 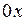 - ось симметрии сечения, оба условия (
- ось симметрии сечения, оба условия ( 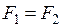 и
и 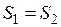 ) дают одинаковый результат.
) дают одинаковый результат.
Дата добавления: 2016-07-27; просмотров: 3355;











