ПРЕДЕЛЬНОГО РАВНОВЕСИЯ

Рассмотренный выше пример показывает, что процесс определения предельной нагрузки даже в простейших статически неопределимых системах представляет достаточно трудоемкую задачу. С целью уменьшения трудоемкости решения данной задачи рекомендуется использовать кинематическую терему предельного равновесия: из всех возможных форм разрушения системы (конструкции) действительной формой является такая, при которой предельная нагрузка является минимальной.

Для иллюстрации данного подхода рассмотрим прежний пример. Так как предельное состояние системы наступает при условии 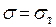в каких-либо двух стержнях, то возможны 3 формы разрушения.

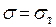1-я форма разрушения - малый поворот балки относительно точки С (рис. 3.5). Состояние наступает в стержнях 1, 2. Так как угол 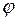- величина малая, то для определения 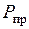можно воспользоваться принципом возможных перемещений:

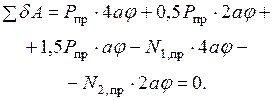
Подставляя сюда 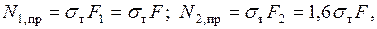получаем уравнение 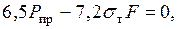из которого следует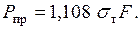

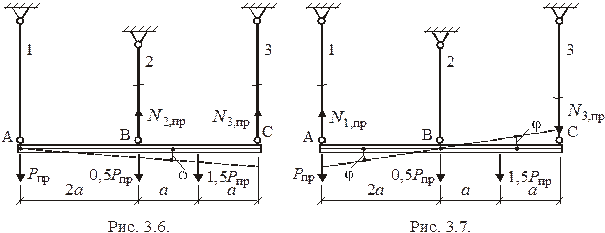
2-я форма разрушения - малый поворот балки относительно точки A (рис. 3.6). Состояние 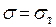наступает в стержнях 2, 3. Для определения 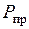воспользуемся принципом возможных перемещений:

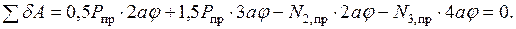
Подставляя сюда 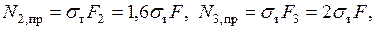получаем уравнение 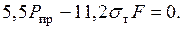Отсюда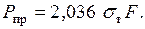

3-я форма разрушения - малый поворот балки относительно точки B (рис. 3.7). Состояние 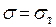наступает в стержнях 1, 3. Составляем уравнение возможных работ:

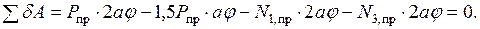
Подставляя сюда 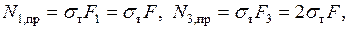получаем уравнение 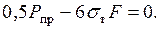Отсюда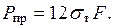

В соответствии с кинематической теоремой предельного равновесия из трех значений 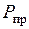выбираем наименьшее значение 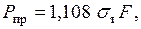соответствующее 1-ой форме разрушения (рис. 3.5).