Линейные коды, обнаруживающие и исправляющие ошибки
Линейными называют коды, в которых проверочные символы представляют собой линейные комбинации информационных символов, т.е. линейные коды являются систематическими.
Основой математического описания линейных кодов является теория алгебраических систем (теория групп, колец, матриц и т.д.).
Кодовые комбинации в линейных кодах рассматриваются как элементы множества.
Алгебраическими системами называют множества, для которых определены некоторые алгебраические операции. Под алгебраической операцией понимается однозначное сопоставление двум элементам третьего элемента по определенным правилам. Обычно такой операцией является сложение ( 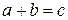 ) или умножение (
) или умножение ( 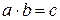 ).
).
Рассмотрим кратко такие алгебраические системы, как группа и кольцо.
Группой называется множество элементов (кодовых комбинаций), объединенных определенным законом композиции. Это значит, что задана некоторая операция 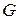 , в результате применения которой к любым двум комбинациям группы образуется третья комбинация, также принадлежащая этой группе. Иными словами, группа – это множество кодовых слов, обладающих свойством замкнутости относительно операции
, в результате применения которой к любым двум комбинациям группы образуется третья комбинация, также принадлежащая этой группе. Иными словами, группа – это множество кодовых слов, обладающих свойством замкнутости относительно операции 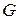 .
.
Группа, состоящая из конечного числа элементов, называется конечной.
Чтобы множество n-разрядных кодовых комбинаций, было конечной группой, при выполнении основной операции число разрядов в результирующей комбинации не должно увеличиваться. Этому условию удовлетворяет операция символического поразрядного сложения по заданному модулю 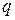 , при которой цифры одинаковых разрядов элементов группы (кодовых комбинаций) складываются обычным порядком, а результатом сложения считается остаток от деления полученного числа на модуль
, при которой цифры одинаковых разрядов элементов группы (кодовых комбинаций) складываются обычным порядком, а результатом сложения считается остаток от деления полученного числа на модуль 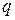 .
.
Дата добавления: 2019-02-08; просмотров: 794;











